大学入試に出題される漸化式に関する問題の中で,漸化式が与えられて,その一般項を求める問題について,漸化式の形で分類すると12のパターンに分けることができました。一部の問題については,定積分で表されていたり,特殊な式で設定されていたりして,分類不能なため,12パターンから除外しています。
2006年~2019年に主要な大学で出題された漸化式の問題は全部で約700問ありました。その中で約530問が漸化式が与えられて一般項を求める問題でした。すべての問題に目を通して,パターンに分類して出題率を算出しました。指導者が異なれば,パターンの分類の仕方も異なるため,あくまでも1つのデータとして,こんな感じで出題されているのかぁと軽い気分で見て下さい。
Contents
- 1 パターン1:等差型・等比型・階差型【出題率5位】
- 2 パターン2:$a_{n+1}=pa_n+q~(p\neq1)$ 型 【出題率3位】
- 3 パターン3:$a_{n+1}=pa_n+f(n)~(p\neq1)$ 型 【出題率1位】
- 4 パターン4:$a_{n+1}=\dfrac{pa_n}{f(n)a_n+q}$ 型 【出題率7位】
- 5 パターン5:$f(n)a_{n+1}a_n=pa_{n+1}+qa_n$ 型 【出題率11位】
- 6 パターン6:$a_{n+2}=pa_{n+1}+qa_n$ 型 【出題率4位】
- 7 パターン7:$a_{n+1}=f(n)a_n+g(n)$ 型 【出題率10位】
- 8 パターン8:数列の項に関する和を含む漸化式 【出題率2位】
- 9 パターン9:数列の項の積・累乗・累乗根を含む漸化式 【出題率9位】
- 10 パターン10:2つの数列の連立漸化式 【出題率6位】
- 11 パターン11:$a_{n+1}=\dfrac{pa_n+q}{ra_n+s}$ 型 【出題率8位】
- 12 パターン12:3つ以上の数列の連立漸化式 【出題率12位】
パターン1:等差型・等比型・階差型【出題率5位】
パターン1はすべての漸化式の基礎となります。等差型・等比型・階差型の3つのタイプがあり,次のように表されます。
&a_{n+1}=a_n+d \\[4pt]
&a_{n+1}=ra_n \\[4pt]
&a_{n+1}=a_n+f(n)
\end{align*}
漸化式の問題が苦手な人は,ここからしっかりと学習していきましょう。出題率は10~12%です。
問題文から漸化式を立てて解く問題だけで見た場合は,出題率は3位で17~20%とかなり多く出題されています。また,漸化式を立てるところまでが重要なので,正確に立式する練習をすることが重要でしょう。

パターン2:$a_{n+1}=pa_n+q~(p\neq1)$ 型 【出題率3位】
パターン2は数ある隣接二項間漸化式の基礎となり,すべてパターン1に変形して解きます。変形方法さえ分かれば機械的に解くことができます。出題率は11~13%です。
問題文から漸化式を立てて解く問題だけで見た場合は,出題率は25~27%で最も多く出題されています。


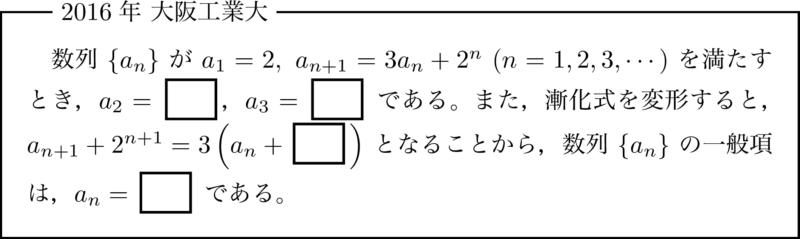
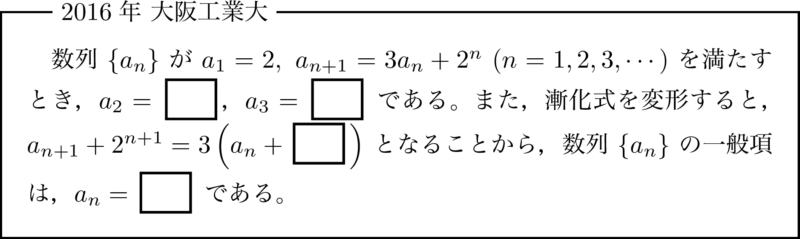
パターン3:$a_{n+1}=pa_n+f(n)~(p\neq1)$ 型 【出題率1位】
パターン3はパターン2の $q$ が定数ではない式で表される漸化式です。$f(n)$ の形によって,対処法が異なりますが,すべてパターン1やパターン2に帰着させて解きます。出題率は14~16%です。






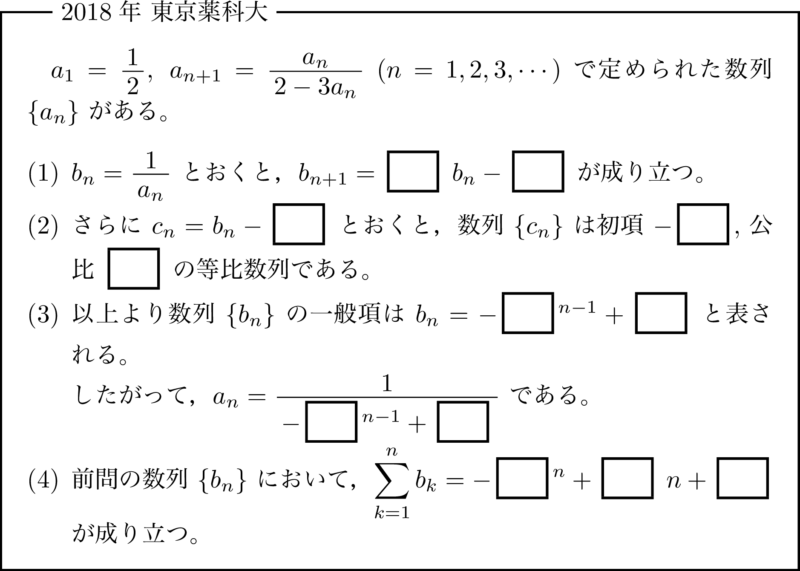
パターン4:$a_{n+1}=\dfrac{pa_n}{f(n)a_n+q}$ 型 【出題率7位】
パターン4は分数式で表される漸化式です。「逆数をとる」ことが解法となります。ただ,逆数をとるために $a_n\neq0$ を証明する必要があります。出題率は6~7%です。

パターン5:$f(n)a_{n+1}a_n=pa_{n+1}+qa_n$ 型 【出題率11位】
基本的に $a_{n+1}a_n$ があればパターン5だと思いましょう。「$a_{n+1}a_n$ で割る」ことが解法となります。このとき,パターン4と同様に $a_n\neq0$ を証明する必要があります。出題率は1~3%と極めて低いです。



パターン6:$a_{n+2}=pa_{n+1}+qa_n$ 型 【出題率4位】
パターン6は $a_{n+2}=pa_{n+1}+qa_n$ で表される隣接三項間漸化式です。特性方程式が2次方程式となり,異なる2解をもつときと重解をもつときで,難易度が少し変わります。
このパターンの応用として,$a_{n+2}=pa_{n+1}+qa_n+f(n)$ で表される問題も出題されます。出題率は10~12%です。







パターン7:$a_{n+1}=f(n)a_n+g(n)$ 型 【出題率10位】
パターン7は二項間漸化式ですが,パターン2の $p$ や $q$ が $n$ の式になっていて,形が似ていても難易度は大きく異なります。入試当日にパターン7を初めて見た場合,かなり苦しむことになるでしょう。出題率は3~5%と低いので,漸化式があまりにも苦手な人は,対策しないという手もあります。









パターン8:数列の項に関する和を含む漸化式 【出題率2位】
パターン8は数列の項の和を含む漸化式です。初項から第 $n$ 項までの和 $S_n$ を含む場合が多いのです。しかし,パターン8の漸化式と気付かせたくないのか,漸化式には $S_n$ を用いず,項を並べて表している問題もあります。また,第 $n-1$ 項までの和を扱ったり,各項を2乗したものの和など様々なタイプがあります。
個人的に,これは厳しい問題だなぁと思うのは,パターン8の解法にしたがって変形するとパターン7になるタイプです。簡単になると思ったら逆に難しくなった,みたいに感じるでしょう。
また,パターン8は様々な問題集やサイトで軽く扱われがちですが,出題率は12~14%でパターン3に次いで多く出題されています。入試では頻出であるにもかかわらず,青チャートの「漸化式MAP」にパターン8は載っていません。意識して対策することが重要かもしれません。















パターン9:数列の項の積・累乗・累乗根を含む漸化式 【出題率9位】
パターン9は $a_n$ の項の累乗を含む漸化式で,よく出題されるのは $a_{n+1}=p{a_n}^q$ のような形です。ただ,いつも二項間漸化式とは限らず,三項間漸化式のタイプもあります。色々なタイプがありますが,ほとんどの問題では対数をとるため,指数関数・対数関数の知識がないと,置換したあとの計算で苦労することになります。出題率は4~6%でそこまで高くありません。





パターン10:2つの数列の連立漸化式 【出題率6位】
パターン10は2つの数列の連立漸化式です。ほとんどの場合は誘導がついた状態で出題されます。しかし,誘導がなければ全く解けないというのでは,確率漸化式の問題で困ることになるでしょう。
一般項を求める問題での出題率は10~12%ですが,自分で漸化式を立式する問題では,パターン2に次ぐ出題率で23~25%と高くなります。正確に連立漸化式を立式できるかが重要であることには違いませんが,立てた漸化式を解けないというのはかなり勿体ない気がします。しっかり対策しておいた方が良いでしょう。








パターン11:$a_{n+1}=\dfrac{pa_n+q}{ra_n+s}$ 型 【出題率8位】
パターン11は分数式で表されるかなり難しい漸化式です。置換方法によって,パターン1,2,4,6,10に変形することができます。すべての解法を知っておけば,苦労することはなくなるでしょう。出題率は5~7%です。






パターン12:3つ以上の数列の連立漸化式 【出題率12位】
パターン12は3つの数列の連立漸化式です。漸化式の知識と方程式を扱う力の両方が問われる問題です。漸化式が与えられて一般項を求める問題としての出題率は約1%で極めて低いのですが,自分で漸化式を立式する問題では,出題率は12~14%になります。したがって,連立漸化式を立てた後,それを解く力があるかどうかで合否が決まってしまう可能性もあります。しっかり対策しておきましょう。