ここでは集合の要素の個数の取り得る値の範囲について説明します。
2つの集合の要素の個数が決まっていても,それら2つの集合の和集合の要素の個数が1つに定まらないものもあります。
値が1つに定まらないような問題を苦手とする人が多いため,解けるようになると有利になることは間違いありません。
苦手な問題を1つずつ克服して総合力をアップさせましょう。
Contents
2つの集合の要素の個数の最大最小問題

ヒロ
それでは実際に定期テストで出題された問題を考えよう。
問題集合 $U$ の2つの部分集合 $A,~B$ に対して,
\begin{align*}
n(U)=50,~n(A)=25,~n(B)=20
\end{align*}
である。このとき,$n(A\cup B)$ の最大値と最小値を求めよ。n(U)=50,~n(A)=25,~n(B)=20
\end{align*}

ヒロ
このタイプの問題では次のポイントが重要となる。
和集合の要素の個数$n(A),~n(B)$ が定数で,$n(A\cup B)$ が最大になるのは,$n(A\cap B)$ が最小になるときである。また,$n(A\cup B)$ が最小になるのは,$n(A\cap B)$ が最大になるときである。

ヒロ
これまで集合を図で表す場合には,ベン図を用いてきたが,ここでは線分を用いて考える方法で考えよう。
集合を線分で表す
集合を表す方法に線分を用いるときのルールは次の通り。
- 集合の要素の個数に応じて線分の長さを適度に変える
- 線分が重なった部分は $n(A\cap B)$ を表す
それでは $n(A\cup B)$ の最大値を考えよう。
【$n(A\cup B)$ の最大値】
数直線を用いて考える。
$n(A\cup B)$ が最大になるのは,$n(A\cap B)$ が最小になるとき,つまり $A$ と $B$ の共通部分が最小になるときである。
したがって,$A$ を表す線分と $B$ を表す線分の重なり部分が最小になるように配置することを考える。
$A$ の線分を左側から右側に伸ばし,$B$ の線分を右側から左側に伸ばすと次の図のように,$A$ と $B$ の共通部分が存在しないことが起こり得ることが分かる。
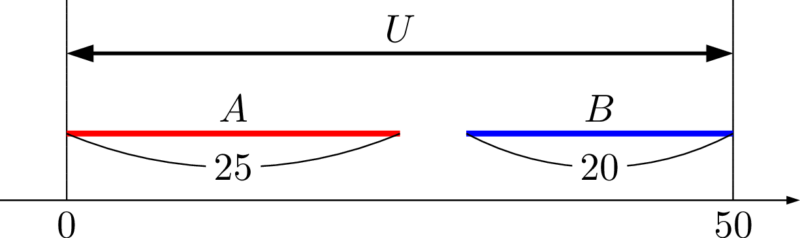
よって,このとき $n(A\cup B)$ は最大となり,最大値は
数直線を用いて考える。
$n(A\cup B)$ が最大になるのは,$n(A\cap B)$ が最小になるとき,つまり $A$ と $B$ の共通部分が最小になるときである。
したがって,$A$ を表す線分と $B$ を表す線分の重なり部分が最小になるように配置することを考える。
$A$ の線分を左側から右側に伸ばし,$B$ の線分を右側から左側に伸ばすと次の図のように,$A$ と $B$ の共通部分が存在しないことが起こり得ることが分かる。

よって,このとき $n(A\cup B)$ は最大となり,最大値は
\begin{align*}
n(A)+n(B)=25+20=45
\end{align*}
n(A)+n(B)=25+20=45
\end{align*}

ヒロ
次に $n(A\cup B)$ の最小値を考えよう。
【$n(A\cup B)$ の最小値】
$n(A\cup B)$ が最小になるのは,$n(A\cap B)$ が最大になるとき,つまり $A$ と $B$ の共通部分が最大になるときである。
したがって,$A$ を表す線分と $B$ を表す線分の重なり部分が最大になるように配置することを考える。
$A,~B$ の両方の線分を左側から右側に伸ばすと次の図のようになる。
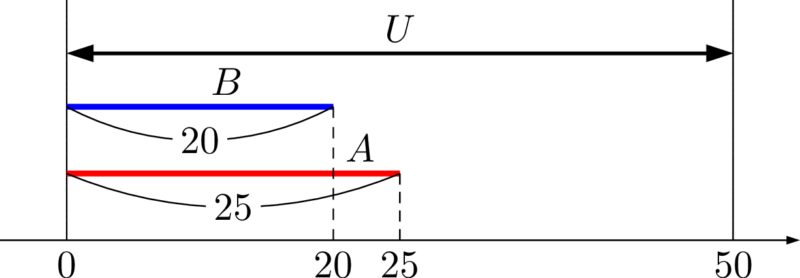
よって,このとき $n(A\cup B)$ は最小となり,最小値は
$n(A\cup B)$ が最小になるのは,$n(A\cap B)$ が最大になるとき,つまり $A$ と $B$ の共通部分が最大になるときである。
したがって,$A$ を表す線分と $B$ を表す線分の重なり部分が最大になるように配置することを考える。
$A,~B$ の両方の線分を左側から右側に伸ばすと次の図のようになる。

よって,このとき $n(A\cup B)$ は最小となり,最小値は
\begin{align*}
n(A)=25
\end{align*}
n(A)=25
\end{align*}

ヒロ
ベン図を用いた説明を読んでも良く分からなかった人も,これで理解できるようになることを望む。


















