【数学IA】さいころの目の最大値・最小値に関する確率

ここではさいころの目の最大値や最小値に関する確率について解説します。

最初は考え方に慣れないかもしれませんが，頑張って身に付けるようにしましょう。

実際に定期テストで出題された問題を用いて説明します。

確実に解けるようにしましょう。

Contents

1 3個のさいころの出る目の最大値が5となる確率
2 3個のさいころの出る目の最小値が3となる確率
3 1個のさいころを3回投げるときの出る目の最大値と最小値に関する確率
4 1個のさいころを $n$ 回投げるときの出る目の最大値と最小値に関する確率

3個のさいころの出る目の最大値が5となる確率

問題3個のさいころを同時に投げるとき，出る目の最大値が次のようになる確率を求めよ。
(1) 5以下
(2) 5

【(1)の考え方と解答】
最大値が5以下となるのは3個すべてのさいころの出る目が5以下のときだから，その確率は

\begin{align*}
\left(\dfrac{5}{6}\right)^3=\dfrac{125}{216}
\end{align*}

(2) 出る目の最大値が5になる確率

【(2)の考え方と解答】
(1)で考えた「最大値が5以下」の中には，次のものが含まれる。

最大値が5
最大値が4
最大値が3
最大値が2
最大値が1

このうち「最大値が5」以外のものは，まとめて「最大値が4以下」と表すことができる。つまり，最大値が5になる確率は最大値が5以下になる確率から最大値が4以下になる確率を引くことで求められる。ベン図を利用した解説をしておくと次のようになる。
3個のさいころの目の最大値が5以下となるさいころの目の集合を $A$ とし，最大値が4以下となるさいころの目の集合を $B$ とすると，集合 $B$ は集合 $A$ に含まれる（$A\supset B$ ）関係にある。ベン図を用いて表すと次のようになる。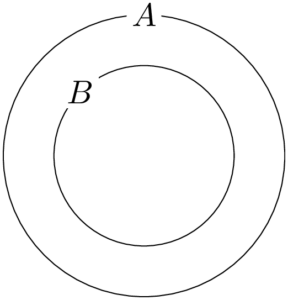

最大値が5となるのは，次の斜線部分である。

3個のさいころの目の最大値が4以下である確率は

\begin{align*}
\left(\dfrac{4}{6}\right)^3=\dfrac{64}{216}
\end{align*}

であるから，求める確率は

\begin{align*}
\dfrac{125}{216}-\dfrac{64}{216}=\dfrac{61}{216}
\end{align*}

3個のさいころの出る目の最小値が3となる確率

問題1個のさいころを3回投げるとき，次の確率を求めよ。
(1) 出る目の最小値が3以上である確率
(2) 出る目の最小値が3である確率

【(1)の考え方と解答】
最小値が3以上となるのは3個すべてのさいころの出る目が3以上のときだから，その確率は

\begin{align*}
\left(\dfrac{4}{6}\right)^3=\dfrac{8}{27}
\end{align*}

(2) 出る目の最小値が3である確率

【(2)の考え方と解答】
出る目の最小値が3となるのは，最小値が3以上の場合から最小値が4以上の場合を除いたものであるから，その確率は

\begin{align*}
&\left(\dfrac{4}{6}\right)^3-\left(\dfrac{3}{6}\right)^3 \\[4pt]
&=\dfrac{64}{216}-\dfrac{27}{216}=\dfrac{37}{216}
\end{align*}

1個のさいころを3回投げるときの出る目の最大値と最小値に関する確率

問題1個のさいころを3回投げるとき，出る目の最大値が5で，最小値が2である確率を求めよ。

【考え方と解答】
1個のさいころを3回投げるとき，目の出方は全部で $6^3=216$ 通りある。これは3回の目の組み合わせが同じでも，出る順番が異なれば別のものとして数えていることに注意しよう。
いま，1個のさいころを3回投げて，出る目の最大値が5で最小値が2ということは，2と5が1回ずつ出る必要がある。残りの1回は2, 3, 4, 5のいずれかである。3回投げたときの出る目を $2,~5,~△$ とすると，出る目の順番に注意すると次の2つに場合分けされる。
　(i) △が2または5のとき
　△の数字の選び方が2通りあり，3つの目の数字の並べ方は，同じ数字が2つあるから $\dfrac{3!}{2!}=3$ 通りである。したがって，目の出方は $2\times3=6$ 通り。
　(ii) △が3または4のとき
　△の数字の選び方が2通りあり，3つの目の数字の並べ方は，異なる3つの数字を並べるから $3!=6$ 通りである。したがって，目の出方は $2\times6=12$ 通り。
(i), (ii)より，条件をみたす目の出方は全部で

\begin{align*}
6+12=18~通り
\end{align*}

となるから，求める確率は

\begin{align*}
\dfrac{18}{216}=\dfrac{1}{12}
\end{align*}

ヒロ

投げる回数が多くなっても対応できるように，別の考え方も理解しておこう。

【別の考え方と解答】
次のように3つの集合を定める。
　$A$ ・・・3回の出る目が2, 3, 4, 5のいずれか
　$B$ ・・・3回の出る目が2, 3, 4のいずれか
　$C$ ・・・3回の出る目が3, 4, 5のいずれか
3つの集合の関係をベン図で表すと次のようになり，出る目の最大値が5で，最小値が2であるのは斜線部分である。

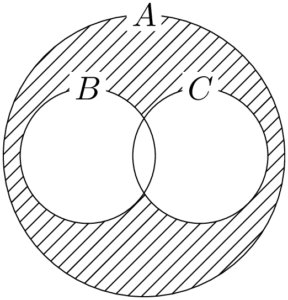
$X$ が起こる確率を $P(X)$ と表すことにすると，求める確率は

\begin{align*}
P(A)-P(B\cup C)
\end{align*}

で求められる。ここで

\begin{align*}
&P(A)=\left(\dfrac{4}{6}\right)^3=\dfrac{64}{216} \\[4pt]
&P(B)=\left(\dfrac{3}{6}\right)^3=\dfrac{27}{216} \\[4pt]
&P(C)=\left(\dfrac{3}{6}\right)^3=\dfrac{27}{216}
\end{align*}

であり，$B\cap C$ は3回の出る目が3, 4のいずれかであるから

\begin{align*}
P(B\cap C)=\left(\dfrac{2}{6}\right)^3=\dfrac{8}{216}
\end{align*}

したがって

\begin{align*}
P(B\cup C)&=P(B)+P(C)-P(B\cap C) \\[4pt]
&=\dfrac{27}{216}+\dfrac{27}{216}-\dfrac{8}{216} \\[4pt]
&=\dfrac{46}{216}
\end{align*}

となる。よって，求める確率は

\begin{align*}
\dfrac{64}{216}-\dfrac{46}{216}&=\dfrac{18}{216} \\[4pt]
&=\dfrac{1}{12}
\end{align*}

1個のさいころを $n$ 回投げるときの出る目の最大値と最小値に関する確率

問題1個のさいころを $n~(n\geqq2)$ 回投げるとき，出る目の最大値が6で，最小値が2である確率を求めよ。

【考え方と解答】
次のように3つの集合を定める。
　$A$ ・・・$n$ 回の出る目が2, 3, 4, 5, 6のいずれか
　$B$ ・・・$n$ 回の出る目が2, 3, 4, 5のいずれか
　$C$ ・・・$n$ 回の出る目が3, 4, 5, 6のいずれか
3つの集合の関係をベン図で表すと次のようになり，出る目の最大値が6で，最小値が2であるのは斜線部分である。

$X$ が起こる確率を $P(X)$ と表すことにすると，求める確率は

\begin{align*}
P(A)-P(B\cup C)
\end{align*}

で求められる。ここで

\begin{align*}
&P(A)=\left(\dfrac{5}{6}\right)^n \\[4pt]
&P(B)=\left(\dfrac{4}{6}\right)^n \\[4pt]
&P(C)=\left(\dfrac{4}{6}\right)^n \\[4pt]
&P(B\cap C)=\left(\dfrac{3}{6}\right)^n
\end{align*}

であるから，

\begin{align*}
P(B\cup C)&=P(B)+P(C)-P(B\cap C) \\[4pt]
&=\left(\dfrac{4}{6}\right)^n+\left(\dfrac{4}{6}\right)^n-\left(\dfrac{3}{6}\right)^n \\[4pt]
&=2\left(\dfrac{4}{6}\right)^n-\left(\dfrac{3}{6}\right)^n
\end{align*}

したがって，求める確率は

\begin{align*}
&\left(\dfrac{5}{6}\right)^n-\left\{2\left(\dfrac{4}{6}\right)^n-\left(\dfrac{3}{6}\right)^n\right\} \\[4pt]
&=\dfrac{5^n-2\Cdot4^n+3^n}{6^n}
\end{align*}