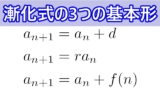前回は漸化式の基本パターンとなる3つのタイプ「等差型・等比型・階差型」について説明しました。
隣り合う二項の間に成り立つ漸化式(隣接二項間漸化式)の基礎と言えるのが,このパターン2となります。
今回の目標は,$a_{n+1}=pa_n+q~(p\neq1)$ で表される漸化式を解けるようになること!
Contents
数列 $\{a_n\}$ の正体
問題条件 $a_1=2,a_{n+1}=3a_n-2$ によって定まる数列 $\{a_n\}$ の一般項を求めよ。
プリントを次のリンクからダウンロードできます。

ヒロ
とりあえず,初項から順に求めてみて?

分かりました。最初が2で,あとは3倍して2を引いていけば良いから・・・
\begin{align*}
2,4,10,28,82,\cdots
\end{align*}
2,4,10,28,82,\cdots
\end{align*}

これくらいで良いですか?

ヒロ
よし。じゃあ今から魔法をかけるよ。各項から1を引いてみて?
\begin{align*}
1,3,9,27,81,\cdots
\end{align*}
1,3,9,27,81,\cdots
\end{align*}

できました。

ヒロ
何か法則はある?

3倍,3倍ってなってるんですね。等比数列です。

ヒロ
ちなみに,その数列の一般項を $b_n$ とすると,$b_n$ はどうなる?

$b_n=3^{n-1}$ となります。

ヒロ
ということは,それに1を加えて $a_n=3^{n-1}+1$ となるってことだね。

ヒロ
よし,これでいいね。って言ったら怒られるよね。ここまでで1つの疑問があるはず。

何故各項から1を引いたのか?ってことですよね。

1ってどこからきたんですか?

ヒロ
そうだね。その魔法の数字である1が分かれば,一般項が簡単に分かるってことだね。