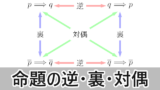
ある命題を証明する際に,そのままでは証明するのが難しかったり,考えにくいときがあります。
そのような場合には,対偶の真偽は元の命題の真偽と一致することを利用して,対偶を証明するのが良いです。
対偶を証明することで,元の命題を証明する方法を学びましょう。
Contents
対偶を利用した命題の証明

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題$x,~y$ がともに正の数であるとき,次の命題を対偶を利用して証明せよ。
$x^2+y^2\geqq10$ ならば「$x\geqq\sqrt{5}$ または $y\geqq\sqrt{5}$」である。
$x^2+y^2\geqq10$ ならば「$x\geqq\sqrt{5}$ または $y\geqq\sqrt{5}$」である。

ヒロ
問題文にあるように対偶を証明することで,元の命題を証明しよう。
【証明】
この命題の対偶は
「$x<\sqrt{5}$ かつ $y<\sqrt{5}$」 ならば $x^2+y^2<10$ である。 $x<\sqrt{5}$ かつ $y<\sqrt{5}$ のとき
この命題の対偶は
「$x<\sqrt{5}$ かつ $y<\sqrt{5}$」 ならば $x^2+y^2<10$ である。 $x<\sqrt{5}$ かつ $y<\sqrt{5}$ のとき
\begin{align*} x^2<5,~y^2<5 \end{align*}
であるから辺々を加えて \begin{align*} x^2+y^2<10 \end{align*}
となり,対偶は真である。 よって,元の命題も真である。対偶に関する問題
問題命題「$a^2+b^2+c^2$ が偶数ならば,$a,~b,~c$ のうち少なくとも1つは偶数である。」$\cdots\cdots$①について次の問いに答えよ。
(1) 命題①の対偶を書け。
(2) 命題①の真偽を答えよ。真ならば証明し,偽ならば反例をあげよ。
(1) 命題①の対偶を書け。
(2) 命題①の真偽を答えよ。真ならば証明し,偽ならば反例をあげよ。

ヒロ
「少なくとも1つ」に注意して対偶を書こう。
【(1)の考え方と解答】
偶数の否定は奇数であるから,「$a^2+b^2+c^2$ が偶数」の否定は「$a^2+b^2+c^2$ が奇数」となる。
「$a,~b,~c$ のうち少なくとも1つは偶数」を言い換えると
「$a$ が偶数 または $b$ が偶数 または $c$ が偶数」
となるから,ド・モルガンの法則よりこの否定は
「$a$ が奇数 かつ $b$ が奇数 かつ $c$ が奇数」
となる。つまり,「$a,~b,~c$ がすべて奇数」となる。
よって,①の対偶は
「$a,~b,~c$ がすべて奇数ならば,$a^2+b^2+c^2$ は奇数である。」
偶数の否定は奇数であるから,「$a^2+b^2+c^2$ が偶数」の否定は「$a^2+b^2+c^2$ が奇数」となる。
「$a,~b,~c$ のうち少なくとも1つは偶数」を言い換えると
「$a$ が偶数 または $b$ が偶数 または $c$ が偶数」
となるから,ド・モルガンの法則よりこの否定は
「$a$ が奇数 かつ $b$ が奇数 かつ $c$ が奇数」
となる。つまり,「$a,~b,~c$ がすべて奇数」となる。
よって,①の対偶は
「$a,~b,~c$ がすべて奇数ならば,$a^2+b^2+c^2$ は奇数である。」

ヒロ
3つの集合のド・モルガンの法則については,次の記事で説明しているので,良く分からない人は参考にして欲しい。

ヒロ
対偶に現れる「奇数」のまま,一般的に考えることができるなら,それで構わない。

ヒロ
一般的に考えることが苦手なら,まずは具体的な値を設定して実験してみると良い。
【具体的な値で実験】
「$a,~b,~c$ がすべて奇数」だから,例えば $a=1,~b=3,~c=7$ としてみると
\begin{align*}
a^2+b^2+c^2&=1^2+3^2+7^2 \\[4pt]
&=1+9+49 \\[4pt]
&=59
\end{align*}
となり,$a^2+b^2+c^2$ は奇数になる。a^2+b^2+c^2&=1^2+3^2+7^2 \\[4pt]
&=1+9+49 \\[4pt]
&=59
\end{align*}

ヒロ
このことがすべての組み合わせについて成り立つならば「この命題は真である」と言える。

ヒロ
1つでもそうならない例(反例)が存在するなら偽となる。

ヒロ
次のことがポイントとなる。
整数の和と積
- $(奇数)+(奇数)=(偶数)$
- $(奇数)+(偶数)=(奇数)$
- $(偶数)+(偶数)=(偶数)$
- $(奇数)\times(奇数)=(奇数)$
- $(奇数)\times(偶数)=(偶数)$
- $(偶数)\times(偶数)=(偶数)$

ヒロ
このことを利用して解答を仕上げよう。
【(2)の解答】
「$a,~b,~c$ がすべて奇数」のとき,$a^2,~b^2,~c^2$ は奇数である。
よって,対偶が真であるので,元の命題①も真である。
「$a,~b,~c$ がすべて奇数」のとき,$a^2,~b^2,~c^2$ は奇数である。
\begin{align*}
a^2+b^2+c^2=(奇数)+(奇数)+(奇数)
\end{align*}
となり,これは奇数である。a^2+b^2+c^2=(奇数)+(奇数)+(奇数)
\end{align*}
よって,対偶が真であるので,元の命題①も真である。

ヒロ
次のように式を使って説明する方法もある。
【(2)の別解】
「$a,~b,~c$ がすべて奇数」のとき,整数 $l,~m,~n$ を用いて
よって,対偶が真であるから,元の命題①も真である。
「$a,~b,~c$ がすべて奇数」のとき,整数 $l,~m,~n$ を用いて
\begin{align*}
&a=2l+1 \\[4pt]
&b=2m+1 \\[4pt]
&c=2n+1
\end{align*}
と表せる。このとき&a=2l+1 \\[4pt]
&b=2m+1 \\[4pt]
&c=2n+1
\end{align*}
\begin{align*}
&a^2+b^2+c^2 \\[4pt]
&=(2l+1)^2+(2m+1)^2+(2n+1)^2 \\[4pt]
&=(4l^2+4l+1)+(4m^2+4m+1)+(4n^2+4n+1) \\[4pt]
&=2(2l^2+2m^2+2n^2+2l+2m+2n+1)+1
\end{align*}
$2l^2+2m^2+2n^2+2l+2m+2n+1$ は整数だから,$a^2,~b^2,~c^2$ は奇数である。&a^2+b^2+c^2 \\[4pt]
&=(2l+1)^2+(2m+1)^2+(2n+1)^2 \\[4pt]
&=(4l^2+4l+1)+(4m^2+4m+1)+(4n^2+4n+1) \\[4pt]
&=2(2l^2+2m^2+2n^2+2l+2m+2n+1)+1
\end{align*}
よって,対偶が真であるから,元の命題①も真である。

ヒロ
「対偶を利用して証明せよ」とあれば,対偶を考えるのは当然であるが,大学入試では,そこまで細かくいってくれないことが多い。

ヒロ
直接証明することが難しく感じるときに,対偶を証明することを考えてみることが重要である。