漸化式パターン10：2つの数列の連立漸化式の解法 part2

漸化式パターン10の第二弾です。2つの数列の連立漸化式という意味では同じですが，その応用として後ろに定数や1次式などがくっつく場合があります。前回説明した連立漸化式になるように，後ろにくっついた項を消すことを考えましょう。

それでは後ろに定数項を含む連立漸化式の問題から解いてみましょう。

2006年兵庫県立大$x_1=4,~y_1=-1$ とし，次の①，②で定められる2つの数列 $\{x_n\},~\{y_n\}$ について，次の問いに答えよ。

\begin{align*}
\begin{cases}
x_{n+1}=4x_n-y_n+1 &~\cdots\cdots① \\[4pt]
y_{n+1}=-x_n+4y_n-3 &~\cdots\cdots②
\end{cases}
\end{align*}

(1) 次の③が成り立つように定数 $a,~p$ を定めよ。

\begin{align*}
x_{n+1}+y_{n+1}-a=p(x_n+y_n-a)~\cdots\cdots③
\end{align*}

(2) 一般項 $x_n,~y_n$ 求めよ。

Contents

1 定数項がある場合
2 1次式がある場合
3 特性方程式の解が複素数
4 練習問題
5 まとめ

定数項がある場合

ヒロ

誘導通り，$x_{n+1}+y_{n+1}-a$ を計算していこう。

【(1)の解答】
①，②より

\begin{align*}
x_{n+1}+y_{n+1}-a&=(4x_n-y_n+1)+(-x_n+4y_n-3)-a \\[4pt]
&=3x_n+3y_n-a-2
\end{align*}

③が成り立つのは，

\begin{align*}
p=3~~かつ~~-a-2=-pa
\end{align*}

のときである。これを解いて，$p=3,~a=1$

ヒロ

(1)の誘導によって，等比型になったから，$x_n+y_n-a$ を $n$ で表そう。

【(2)の解答】
(1)の結果より，数列 $\{x_n+y_n-1\}$ は公比3の等比数列と分かるから，

\begin{align*}
&x_n+y_n-1=(x_1+y_1-1)\Cdota3^{n-1} \\[4pt]
&x_n+y_n-1=2\Cdota3^{n-1}~\cdots\cdots④
\end{align*}

ヒロ

同じようにして，もう1本作ろう。

ヒロ

前回扱った連立漸化式は特性方程式を解くことで等比型になったけど，定数項が残ったところでパターン2になるわけで，特には困らないよね。

ヒロ

ということで具体的に話を進めるよ。連立漸化式の定数項がない場合の特性方程式を解いてみよう。

特性方程式 $x=\dfrac{4x-1}{-x+4}$ を解くと

\begin{align*}
&x(-x+4)=4x-1 \\[4pt]
&x^2=1 \\[4pt]
&x=\pm1
\end{align*}

ヒロ

定数項がなかったときは，$\{x_n+y_n\}$ と $\{x_n-y_n\}$ が等比型になったね。定数項がある場合はどうなるか，実際に計算して確認してみよう。

$x_{n+1}+y_{n+1}$ を計算すると

\begin{align*}
x_{n+1}+y_{n+1}&=(4x_n-y_n+1)+(-x_n+4y_n-3) \\[4pt]
&=3(x_n+y_n)-2
\end{align*}

$x_{n+1}-y_{n+1}$ を計算すると

\begin{align*}
x_{n+1}-y_{n+1}&=(4x_n-y_n+1)-(-x_n+4y_n-3) \\[4pt]
&=5(x_n-y_n)+4
\end{align*}

ヒロ

このように，定数項が残ってパターン2になるだけだね。パターン2からさらに変形した等比型にするためのヒントを与えるのが最初の誘導だったということ。これで仕組みが分かったから一気に解いてしまおう。

【(2)の解答の続き】
①，②より

\begin{align*}
&x_{n+1}-y_{n+1}=(4x_n-y_n+1)-(-x_n+4y_n-3) \\[4pt]
&x_{n+1}-y_{n+1}=5(x_n-y_n)+4 \\[4pt]
&x_{n+1}-y_{n+1}+1=5(x_n-y_n+1)
\end{align*}

数列 $\{x_n-y_n+1\}$ は公比5の等比数列であるから

\begin{align*}
&x_n-y_n+1=(x_1-y_1+1)\Cdota5^{n-1} \\[4pt]
&x_n-y_n+1=6\Cdota5^{n-1}~\cdots\cdots⑤
\end{align*}

$\dfrac{④+⑤}{2}$ より

\begin{align*}
x_n=3^{n-1}+3\Cdota5^{n-1}
\end{align*}

$④-⑤$ より

\begin{align*}
&2y_n-2=2\Cdota3^{n-1}-6\Cdota5^{n-1} \\[4pt]
&y_n=3^{n-1}-3\Cdota5^{n-1}+1
\end{align*}

1次式がある場合

ヒロ

次の問題を解いてみよう。

2007年熊本大数列 $\{x_n\}$ および $\{y_n\}$ は以下の条件を満たしているものとする。

\begin{align*}
&x_1=8,~y_1=-5 \\[4pt]&x_{n+1}=2x_n+y_n+3n-8~(n=1,2,3,\cdots) \\[4pt]&y_{n+1}=2y_n+x_n-3n+8~(n=1,2,3,\cdots)
\end{align*}

以下の問いに答えよ。
(1) $z_n=x_n+y_n$ ，また $w_n=x_n-y_n$ とおく。数列 $\{z_n\}$ および $\{w_n\}$ の一般項を求めよ。
(2) $xy$ 平面上の点 $(x_n,~y_n)$ と直線 $y=x$ との距離が最小になるような $n$ の値をすべて求めよ。

ヒロ

まずは $z_n,~w_n$ の漸化式を立てよう。

【(1) $z_n$ を求める】
与えられた漸化式より

\begin{align*}
z_{n+1}&=x_{n+1}+y_{n+1} \\[4pt]&=(2x_n+y_n+3n-8)+(2y_n+x_n-3n+8) \\[4pt]&=3(x_n+y_n) \\[4pt]&=3z_n
\end{align*}

数列 $\{z_n\}$ は公比3の等比数列であり，

\begin{align*}
z_1=x_1+y_1=3
\end{align*}

であるから

\begin{align*}
z_n=3^{n}
\end{align*}

ヒロ

これで $z_n$ を求めることができた。後ろにくっついてる $n$ の1次式がすべて消えて，等比型になったので楽だったね。同じようにして $w_n$ も求めよう。

【(1) $w_n$ を求める】
与えられた漸化式より

\begin{align*}
w_{n+1}&=x_{n+1}-y_{n+1} \\[4pt]&=(2x_n+y_n+3n-8)-(2y_n+x_n-3n+8) \\[4pt]&=x_n-y_n+6n-16 \\[4pt]&=w_n+6n-16
\end{align*}

よって，$n\geqq2$ のとき

\begin{align*}
w_n&=w_1+\Sum{k=1}{n-1}(6k-16) \\[4pt]&=x_1-y_1+\dfrac{-10+(6n-22)}{2}\Cdot(n-1) \\[4pt]&=13+(3n-16)(n-1) \\[4pt]&=3n^2-19n+29
\end{align*}

これは $n=1$ のときも成り立つ。

ヒロ

これで $w_n$ も求めることができた。階差型の解法を理解していればこれも簡単に求められたはず。

ヒロ

(2)はまず，点 $(x_n,~y_n)$ と直線 $y=x$ の距離がどんな式なのかを調べよう。

【(2)の解答】
点 $(x_n,~y_n)$ と直線 $y=x$ の距離を $d_n$ とすると，

\begin{align*}
d_n&=\dfrac{\abs{x_n-y_n}}{\sqrt{2}} \\[4pt]&=\dfrac{\abs{w_n}}{\sqrt{2}} \\[4pt]&=\dfrac{\abs{3n^2-19n+29}}{\sqrt{2}}
\end{align*}

ヒロ

あとは分子が最小になるような自然数 $n$ の値を求めれば終わりだね。

【(2)の解答の続き】
$f(n)=3n^2-19n+29$ とすると，$y=\abs{f(x)}$ のグラフは次のようになる。

\begin{align*}
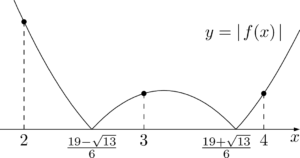
\abs{f(3)}=\abs{27-57+29}=1 \\[4pt]\abs{f(4)}=\abs{48-76+29}=1
\end{align*}

であるから，グラフより求める自然数 $n$ の値は，$n=3,~4$

特性方程式の解が複素数

ヒロ

次の問題を解いてみよう。

2017年群馬大・医$\theta_n=\dfrac{5\pi}{6n(n+1)}$$~(n=1,2,3,\cdots)$ とする。数列 $\{a_n\},~\{b_n\}$ は，初項がそれぞれ $a_1=\cos\theta_1,~$$b_1=\sin\theta_1$ で与えられ，漸化式

\begin{align*}
a_{n+1}=a_n\cos\theta_{n+1}-b_n\sin\theta_{n+1} \\[4pt]
b_{n+1}=a_n\sin\theta_{n+1}+b_n\cos\theta_{n+1}
\end{align*}

を満たす。
(1) $\{a_n\},~\{b_n\}$ の一般項を求めよ。
(2) 数列 $\{a_n\},~\{b_n\}$ の極限を求めよ。

ヒロ

連立漸化式で誘導がないタイプ。この場合，$a_2,~b_2,~$$a_3,~b_3$ と求めていって，それらの値から $a_n$ を推測して，数学的帰納法で証明するか，特性方程式を利用することで解ける形へ変形するかのいずれかの方法で解くしかない。

ヒロ

ここでは両方の解法を紹介しておく。

推測して証明する

漸化式より

\begin{align*}
a_2&=a_1\cos\theta_2-b_1\sin\theta_2 \\[4pt]
&=\cos\theta_1\cos\theta_2-\sin\theta_1\sin\theta_2 \\[4pt]
&=\cos(\theta_1+\theta_2) \\[4pt]
b_2&=a_1\sin\theta_2+b_1\cos\theta_2 \\[4pt]
&=\cos\theta_1\sin\theta_2+\sin\theta_1\cos\theta_2 \\[4pt]
&=\sin(\theta_1+\theta_2) \\[4pt]
a_3&=a_2\cos\theta_3-b_2\sin\theta_3 \\[4pt]
&=\cos(\theta_1+\theta_2)\cos\theta_3-\sin(\theta_1+\theta_2)\sin\theta_3 \\[4pt]
&=\cos(\theta_1+\theta_2+\theta_3) \\[4pt]
b_3&=a_2\sin\theta_3+b_2\cos\theta_3 \\[4pt]
&=\cos(\theta_1+\theta_2)\sin\theta_3+\sin(\theta_1+\theta_2)\cos\theta_3 \\[4pt]
&=\sin(\theta_1+\theta_2+\theta_3)
\end{align*}

ヒロ

それぞれにおいて，最後の変形は三角関数の加法定理を利用している。

加法定理

\begin{align*}
&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \\[4pt]
&\cos(\alpha+\beta)=\cos\alpha\sin\beta+\sin\alpha\cos\beta
\end{align*}

ヒロ

これで $a_n,~b_n$ がどんな式か推測できるね。

$a_n,~b_n$ は次のようになると推測できる。

\begin{align*}
&a_n=\cos(\theta_1+\theta_2+\cdots+\theta_n) \\[4pt]
&b_n=\sin(\theta_1+\theta_2+\cdots+\theta_n)
\end{align*}

ヒロ

これで解答の準備が整った。

【(1)の解答】
すべての自然数 $n$ に対して

\begin{align*}
a_n=\cos\phi_n,~b_n=\sin\phi_n~\cdots\cdots①
\end{align*}

と表すことができることを数学的帰納法で証明する。
(i) $n=1$ のとき

\begin{align*}
a_1=\cos\theta_1,~b_1=\sin\theta_1
\end{align*}

であるから，$\phi_1=\theta_1$ とすれば①は成り立つ。
(ii) $a_k=\cos\phi_k,~b_k=\sin\phi_k$ と表すことができると仮定すると

\begin{align*}
a_{k+1}&=a_k\cos\theta_{k+1}-b_k\sin\theta_{k+1} \\[4pt]
&=\cos\phi_k\cos\theta_{k+1}-\sin\phi_k\sin\theta_{k+1} \\[4pt]
&=\cos(\phi_k+\theta_{k+1}) \\[4pt]
b_{k+1}&=a_k\sin\theta_{k+1}+b_k\cos\theta_{k+1} \\[4pt]
&=\cos\phi_k\sin\theta_{k+1}+\sin\phi_k\cos\theta_{k+1} \\[4pt]
&=\sin(\phi_k+\theta_{k+1})
\end{align*}

よって，$\phi_{k+1}=\phi_k+\theta_{k+1}$ とすれば，$n=k+1$ のときも①は成り立つ。
(i)，(ii)より，すべての自然数 $n$ に対して①は成り立つ。
ここで

\begin{align*}
\phi_1=\theta_1,~\phi_{n+1}=\phi_n+\theta_{n+1}
\end{align*}

であるから

\begin{align*}
\phi_n&=\phi_1+\Sum{k=2}{n}\theta_k \\[4pt]
&=\Sum{k=1}{n}\theta_k \\[4pt]
&=\Sum{k=1}{n}\dfrac{5\pi}{6k(k+1)} \\[4pt]
&=\dfrac{5\pi}{6}\Sum{k=1}{n}\left(\dfrac{1}{k}-\dfrac{1}{k+1}\right) \\[4pt]
&=\dfrac{5\pi}{6}\left(1-\dfrac{1}{n+1}\right) \\[4pt]
&=\dfrac{5n\pi}{6(n+1)}
\end{align*}

よって，

\begin{align*}
a_n=\cos\dfrac{5n\pi}{6(n+1)},~b_n=\sin\dfrac{5n\pi}{6(n+1)}
\end{align*}

特性方程式を利用する

$\cos\theta_{n+1}=c,~\sin\theta_{n+1}=s$ とおいて，特性方程式 $x=\dfrac{cx-s}{sx+c}$ を解くと

\begin{align*}
&x(sx+c)=cx-s \\[4pt]
&sx^2=-s
\end{align*}

ここで

\begin{align*}
s&=\sin\theta_{n+1} \\[4pt]
&=\sin\dfrac{5\pi}{6(n+1)(n+2)}\neq0
\end{align*}

であるから

\begin{align*}
&x^2=-1 \\[4pt]
&x=\pm i
\end{align*}

ヒロ

虚数単位 $i$ を含む方程式が1本あれば，実部と虚部で2本の方程式を立てることができるから，片方だけで解けるはず。ということで，$a_{n+1}+ib_{n+1}$ を計算してみよう。

【(1)の別解】
与えられた漸化式より

\begin{align*}
a_{n+1}+ib_{n+1}&=(a_n\cos\theta_{n+1}-b_n\sin\theta_{n+1})+i(a_n\sin\theta_{n+1}+b_n\cos\theta_{n+1}) \\[4pt]
&=a_n(\cos\theta_{n+1}+i\sin\theta_{n+1})+ib_n(\cos\theta_{n+1}+i\sin\theta_{n+1}) \\[4pt]
&=(\cos\theta_{n+1}+i\sin\theta_{n+1})(a_n+ib_n)
\end{align*}

ここで $z_n=\cos\theta_n+i\sin\theta_n$ とおくと

\begin{align*}
a_{n+1}+ib_{n+1}&=z_{n+1}(a_n+ib_n)
\end{align*}

となる。

ヒロ

これで漸化式の形としては，パターン7だね。繰り返し用いることで添字を1にしよう。

$a_{n+1}+ib_{n+1}=z_{n+1}(a_n+ib_n)$ より

\begin{align*}
a_n+ib_n&=z_n(a_{n-1}+ib_{n-1}) \\[4pt]
&=z_nz_{n-1}(a_{n-2}+ib_{n-2}) \\[4pt]
&=z_nz_{n-1}z_{n-2}(a_{n-3}+ib_{n-3}) \\[4pt]
&\qquad\vdots \\[4pt]
&=z_nz_{n-1}\cdots z_2(a_1+ib_1)
\end{align*}

$a_1+ib_1=\cos\theta_1+i\sin\theta_1=z_1$ より

\begin{align*}
a_n+ib_n=z_1z_2\cdots z_n
\end{align*}

ヒロ

あとは極形式の積の性質を利用して求めよう。

極形式の積

複素数 $z_1=r_1(\cos\theta_1+i\sin\theta_1),~$$z_2=r_2(\cos\theta_2+i\sin\theta_2)$ に対して

\begin{align*}
z_1z_2=r_1r_2\{\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\}
\end{align*}

が成り立つ。

【(1)の別解の続き】
これを繰り返し用いることによって

\begin{align*}
a_n+ib_n=z_1z_2\cdots z_n
\end{align*}

となる。ここで

\begin{align*}
\arg z_k&=\theta_k=\dfrac{5\pi}{6k(k+1)} \\[4pt]
&=\dfrac{5\pi}{6}\left(\dfrac{1}{k}-\dfrac{1}{k+1}\right)
\end{align*}

であるから

\begin{align*}
\Sum{k=1}{n}\arg z_k&=\Sum{k=1}{n}\dfrac{5\pi}{6}\left(\dfrac{1}{k}-\dfrac{1}{k+1}\right) \\[4pt]
&=\dfrac{5\pi}{6}\left(1-\dfrac{1}{n+1}\right) \\[4pt]
&=\dfrac{5n\pi}{6(n+1)}
\end{align*}

したがって，

\begin{align*}
a_n+ib_n=\cos\dfrac{5n\pi}{6(n+1)}+i\sin\dfrac{5n\pi}{6(n+1)}
\end{align*}

となるから

\begin{align*}
a_n=\cos\dfrac{5n\pi}{6(n+1)},~b_n=\sin\dfrac{5n\pi}{6(n+1)}
\end{align*}

(2)の解答

ヒロ

(2)の極限の問題は(1)が解けた人へのボーナス問題だね。

【(2)の解答】
$\dlim{n\to\infty}\dfrac{5\pi}{6}\left(1-\dfrac{1}{n+1}\right)=\dfrac{5\pi}{6}$ より

\begin{align*}
&\dlim{n\to\infty}a_n=\cos\dfrac{5\pi}{6}=-\dfrac{\sqrt{3}}{2} \\[4pt]
&\dlim{n\to\infty}b_n=\sin\dfrac{5\pi}{6}=\dfrac{1}{2}
\end{align*}

ヒロ

ちなみに医学部以外の学部では，漸化式自体は同じもので，次のように，$\theta_n$ の定義が異なる問題になっている。

2017年群馬大$\theta_n=\dfrac{\pi}{4n(n+1)}$
(1) $a_2,~b_2$ の値を求めよ。
(2) 数列 $\{a_n\},~\{b_n\}$ の一般項を求めよ。

ヒロ

(1)で $a_2,~b_2$ を求めさせているから，そこから推測できないと解くのは厳しいだろう。

練習問題

ヒロ

それでは練習として次の問題を解いてみよう。

2019年大分大次の条件によって定められる数列 $\{a_n\},~\{b_n\}$ がある。

\begin{align*}
&a_1=3,~b_1=1 \\[4pt]
&2a_{n+1}=5a_n+b_n+2^{n+1}+4~(n=1,2,3,\cdots) \\[4pt]
&2b_{n+1}=a_n+5b_n-2^{n+1}+4~(n=1,2,3,\cdots)
\end{align*}

(1) $c_n=a_n+b_n$ によって定められる数列 $\{c_n\}$ を $n$ の式で表しなさい。
(2) $d_n=a_n-b_n$ によって定められる数列 $\{d_n\}$ を $n$ の式で表しなさい。
(3) 数列 $\{a_n\}$ に一般項 $a_n$ を $n$ の式で表しなさい。
(4) 数列 $\{a_n\}$ の初項から第 $n$ 項までの和を $S_n$ とする。$S_n$ を $n$ の式で表しなさい。

ヒロ

(1)は $\{c_n\}$ の漸化式を立ててそれを解くことで $c_n$ を求めよう。

【(1)の解答】
与えられた漸化式より

\begin{align*}
c_{n+1}&=a_{n+1}+b_{n+1} \\[4pt]
&=\left(\dfrac{5}{2}a_n+\dfrac{1}{2}b_n+2^n+2\right)+\left(\dfrac{1}{2}a_n+\dfrac{5}{2}b_n-2^n+2\right) \\[4pt]
&=3(a_n+b_n)+4 \\[4pt]
&=3c_n+4
\end{align*}

これを変形すると

\begin{align*}
c_{n+1}+2=3(c_n+2)
\end{align*}

となるから，数列 $\{c_n+2\}$ は公比3の等比数列である。

\begin{align*}
c_1+2=a_1+b_1+2=6
\end{align*}

であるから

\begin{align*}
&c_n+2=(c_1+2)\Cdota3^{n-1} \\[4pt]
&c_n+2=6\Cdota3^{n-1} \\[4pt]
&c_n=2\Cdot3^n-2
\end{align*}

ヒロ

(2)は(1)と同様に解いていこう。

【(2)の解答】
与えられた漸化式より

\begin{align*}
d_{n+1}&=a_{n+1}-b_{n+1} \\[4pt]
&=\left(\dfrac{5}{2}a_n+\dfrac{1}{2}b_n+2^n+2\right)-\left(\dfrac{1}{2}a_n+\dfrac{5}{2}b_n-2^n+2\right) \\[4pt]
&=2(a_n-b_n)+2^{n+1} \\[4pt]
&=2d_n+2^{n+1}
\end{align*}

両辺を $2^{n+1}$ で割ると

\begin{align*}
&\dfrac{d_{n+1}}{2^{n+1}}=\dfrac{d_n}{2^n}+1
\end{align*}

となるから，数列 $\left\{\dfrac{d_n}{2^n}\right\}$ は公差1の等差数列である。

\begin{align*}
\dfrac{d_1}{2}=\dfrac{a_1-b_1}{2}=1
\end{align*}

であるから

\begin{align*}
&\dfrac{d_n}{2^n}=n \\[4pt]
&d_n=n\Cdota2^n
\end{align*}

ヒロ

$a_n$ は(1)と(2)を連立して求めよう。

【(3)の解答】
(1)，(2)の結果より

\begin{align*}
&a_n+b_n=2\Cdot3^n-2 &~\cdots\cdots① \\[4pt]
&a_n-b_n=n\Cdota2^n &~\cdots\cdots②
\end{align*}

$\dfrac{①+②}{2}$より

\begin{align*}
a_n=3^n+n\Cdota2^{n-1}-1
\end{align*}

ヒロ

(4)は落ち着いて計算しよう。

【(4)の解答】
(3)の結果より

\begin{align*}
S_n&=\Sum{k=1}{n}(3^k+k\Cdota2^{k-1}-1)
\end{align*}

ここで $f(k)=(k-2)\Cdot2^{k-1}$ とおくと，

\begin{align*}
f(k+1)-f(k)&=(k-1)\Cdota2^k-(k-2)\Cdota2^{k-1} \\[4pt]
&=\{2(k-1)-(k-2)\}\Cdota2^{k-1} \\[4pt]
&=k\Cdota2^{k-1}
\end{align*}

となるから

\begin{align*}
\Sum{k=1}{n}k\Cdota2^{k-1}&=\Sum{k=1}{n}\{f(k+1)-f(k)\} \\[4pt]
&=f(n+1)-f(1) \\[4pt]
&=(n-1)\Cdota2^n+1~\cdots\cdots③
\end{align*}

また

\begin{align*}
\Sum{k=1}{n}(3^k-1)&=\dfrac{3(3^n-1)}{3-1}-n \\[4pt]
&=\dfrac{3^{n+1}}{2}-n-\dfrac{3}{2}~\cdots\cdots④
\end{align*}

であるから，$③+④$ より

\begin{align*}
S_n=\dfrac{3^{n+1}}{2}+(n-1)\Cdota2^n-n-\dfrac{1}{2}
\end{align*}

ヒロ

$\Sum{k=1}{n}k\Cdota2^{k-1}$ は等差数列と等比数列の積の和であるから，通常は「公比を掛けて引く」という方法で求める。しかし，ここでは $k\Cdot2^{k-1}$ を差の形で表す方法で求めている。

【$f(k)$ の求め方】
$f(k)=(ak+b)\Cdot2^{k-1}$ とおくと

\begin{align*}
f(k+1)-f(k)&=(ak+a+b)\Cdota2^k-(ak+b)\Cdot2^{k-1} \\[4pt]
&=\{2(ak+a+b)-(ak+b)\}\Cdota2^{k-1} \\[4pt]
&=(ak+2a+b)\Cdota2^{k-1}
\end{align*}

これが $k\Cdot2^{k-1}$ となるときを考えて

\begin{align*}
&a=1~~かつ~~2a+b=0 \\[4pt]
&a=1,~b=-2
\end{align*}

よって，$f(k)=(k-2)\Cdot2^{k-1}$