ここでは三角形の成立条件に関する問題を解説します。
三角形の3つの辺の長さは好きなように設定することはできません。
例えば長さが1, 1, 2の3本の線分からは三角形を作ることはできません。
したがって,3本の線分から三角形を作ることができるときには,その線分の長さには何らかの条件があるはずです。
それが三角形の成立条件と呼ばれるものです。
この記事を読むことで,その三角形の成立条件がどんなものかを知り,使いこなせるようになります。
Contents
- ページ1
- 1 三角形の成立条件
- ページ2
- 1 三角形の成立条件に関する問題
- ページ3
- 1 鋭角三角形となる条件に関する問題
三角形の成立条件

ヒロ
三角形を作るためには3本の線分の長さにどのような条件が必要かを考えてみよう。
【三角形の成立条件を考える】
$\sankaku{ABC}$ の3辺の長さが $a,~b,~c$ となるための条件を考えよう。
まず,BCを底辺として,残り2辺AB, ACの長さ $b,~c$ の条件を考える。

長さが $b,~c$ である2本の線分を用意する。
例えば,$b,~c$ が次の図のようになっているとき,$b,~c$ の長さが足りず三角形を作ることはできない。

三角形を作るためには $b$ と $c$ の和が $a$ より大きくなる必要がある。
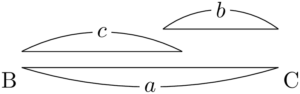
上の図のようになっていると,次の図のように三角形を作ることができる。

つまり
このことはABやCAを底辺にしても同様の不等式,すなわち
②より,$a>c-b$
③より,$a>b-c$
②と③の2本の不等式は,実は1本しか意味がないことが分かる。
$c-b$ と $b-c$ は引く順序が異なるだけだから,$b$ と $c$ が異なるとき,一方が正でもう一方が負である。$b$ と $c$ が等しいときは $a>0$ という「辺の長さ $a$ は正である」という当然とも言える不等式になる。
したがって,$b-c$ と $c-b$ のうち,0以上の方を採用すればよいことになる。つまり $b-c$ の絶対値を利用すれば良く,$a>c-b$ と $a>b-c$ は $a>\abs{b-c}$ という1本の不等式にまとめることができる。
よって,①~③は
$\sankaku{ABC}$ の3辺の長さが $a,~b,~c$ となるための条件を考えよう。
まず,BCを底辺として,残り2辺AB, ACの長さ $b,~c$ の条件を考える。
長さが $b,~c$ である2本の線分を用意する。
例えば,$b,~c$ が次の図のようになっているとき,$b,~c$ の長さが足りず三角形を作ることはできない。

三角形を作るためには $b$ と $c$ の和が $a$ より大きくなる必要がある。

上の図のようになっていると,次の図のように三角形を作ることができる。

つまり
\begin{align*}
b+c>a~\cdots\cdots①
\end{align*}
という不等式が成り立つ必要がある。b+c>a~\cdots\cdots①
\end{align*}
このことはABやCAを底辺にしても同様の不等式,すなわち
\begin{align*}
a+b>c~\cdots\cdots②~かつ~c+a>b~\cdots\cdots③
\end{align*}
が成り立つ必要がある。①~③が三角形の成立条件となるが,もう少し整理することで2本の不等式にすることができる。a+b>c~\cdots\cdots②~かつ~c+a>b~\cdots\cdots③
\end{align*}
②より,$a>c-b$
③より,$a>b-c$
②と③の2本の不等式は,実は1本しか意味がないことが分かる。
$c-b$ と $b-c$ は引く順序が異なるだけだから,$b$ と $c$ が異なるとき,一方が正でもう一方が負である。$b$ と $c$ が等しいときは $a>0$ という「辺の長さ $a$ は正である」という当然とも言える不等式になる。
したがって,$b-c$ と $c-b$ のうち,0以上の方を採用すればよいことになる。つまり $b-c$ の絶対値を利用すれば良く,$a>c-b$ と $a>b-c$ は $a>\abs{b-c}$ という1本の不等式にまとめることができる。
よって,①~③は
\begin{align*} b+c>a~かつ~a>\abs{b-c} \end{align*}
となり \begin{align*} \abs{b-c}<a<b+c \end{align*}
と表すこともできる。三角形の成立条件$a,~b,~c$ が三角形の3辺となるための条件は
\begin{align*} \abs{b-c}<a<b+c \end{align*}
が成り立つことである。



















