ここでは三角比を利用して空間図形の問題を解く方法について説明します。
問題に出てくる空間図形として,直方体・立方体・三角錐(四面体)・球・円錐などがあります。
どのような空間図形であっても,平面で切断したときに現れる切断面を捉えて,平面図形の問題として解くことが重要です。
問題が複雑になると,様々な平面に着目する必要があるため「こういう問題はこう解く」といったパターンで覚えて解いている人にとっては難しく感じるでしょう。
問われている値を求めるために,何を求める必要があるか,またそのためにはどの平面で考えるのが良いのかを丁寧に考えましょう。
直方体と三角比

ヒロ
直方体に関する問題が広島工業大で出題されている。
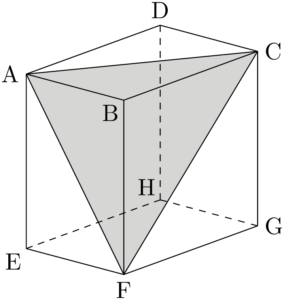
2019年 広島工業大直方体ABCD-EFGHにおいて,$\text{AB}=1$, $\text{AD}=\sqrt{2}$, $\text{AE}=\sqrt{3}$ とする。このとき,$\sankaku{ACF}$ の面積を求めよ。
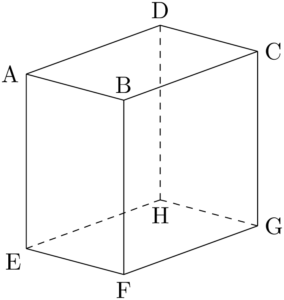

【考え方と解答】
三角形ACFの面積を求めるために,3辺AC, AF, CFの長さを求めよう。空間図形において辺の長さを求めるときは,その辺を含む平面に着目しよう。つまりACの長さを求めるときは,直方体の上面ABCDに着目しよう。
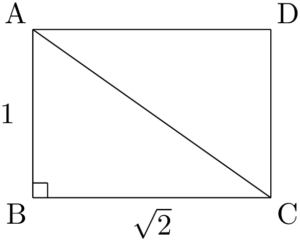
四角形ABCDは長方形だから,三平方の定理より

三平方の定理より
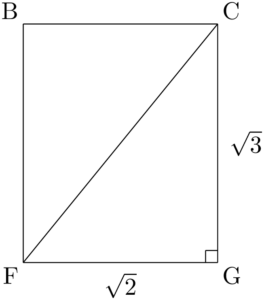
三平方の定理より
斜めから見た状態で考えるのが苦手な人は,面倒でも次のように $\sankaku{ACF}$ を取り出して考えよう。

$\kaku{AFC}=\theta$ とすると,余弦定理より
三角形ACFの面積を求めるために,3辺AC, AF, CFの長さを求めよう。空間図形において辺の長さを求めるときは,その辺を含む平面に着目しよう。つまりACの長さを求めるときは,直方体の上面ABCDに着目しよう。

四角形ABCDは長方形だから,三平方の定理より
\begin{align*}
\text{AC}=\sqrt{1^2+(\sqrt{2})^2}=\sqrt{3}
\end{align*}
次にAFの長さを求めるために,側面AEFBに着目する。\text{AC}=\sqrt{1^2+(\sqrt{2})^2}=\sqrt{3}
\end{align*}

三平方の定理より
\begin{align*}
\text{AF}=\sqrt{(\sqrt{3})^2+1^2}=2
\end{align*}
CFの長さを求めるために,側面BFGCに着目する。\text{AF}=\sqrt{(\sqrt{3})^2+1^2}=2
\end{align*}

三平方の定理より
\begin{align*}
\text{CF}=\sqrt{(\sqrt{3})^2+(\sqrt{2})^2}=\sqrt{5}
\end{align*}
三角形ACFの3辺の長さが分かったから,1つの内角に着目して,余弦定理でコサインを求めよう。\text{CF}=\sqrt{(\sqrt{3})^2+(\sqrt{2})^2}=\sqrt{5}
\end{align*}

斜めから見た状態で考えるのが苦手な人は,面倒でも次のように $\sankaku{ACF}$ を取り出して考えよう。

$\kaku{AFC}=\theta$ とすると,余弦定理より
\begin{align*}
\cos\theta&=\dfrac{2^2+(\sqrt{5})^2-(\sqrt{3})^2}{2\Cdot2\sqrt{5}} \\[4pt]
&=\dfrac{6}{4\sqrt{5}}=\dfrac{3}{2\sqrt{5}}
\end{align*}
$\sin\theta>0$ であるから\cos\theta&=\dfrac{2^2+(\sqrt{5})^2-(\sqrt{3})^2}{2\Cdot2\sqrt{5}} \\[4pt]
&=\dfrac{6}{4\sqrt{5}}=\dfrac{3}{2\sqrt{5}}
\end{align*}
\begin{align*}
\sin\theta&=\sqrt{1-\cos^2\theta} \\[4pt]
&=\sqrt{1-\left(\dfrac{3}{2\sqrt{5}}\right)^2} \\[4pt]
&=\dfrac{\sqrt{11}}{2\sqrt{5}}
\end{align*}
したがって\sin\theta&=\sqrt{1-\cos^2\theta} \\[4pt]
&=\sqrt{1-\left(\dfrac{3}{2\sqrt{5}}\right)^2} \\[4pt]
&=\dfrac{\sqrt{11}}{2\sqrt{5}}
\end{align*}
\begin{align*}
\sankaku{ACF}&=\dfrac{1}{2}\text{AF}\Cdota\text{CF}\sin\theta \\[4pt]
&=\dfrac{1}{2}\Cdota2\sqrt{5}\Cdota\dfrac{\sqrt{11}}{2\sqrt{5}} \\[4pt]
&=\dfrac{\sqrt{11}}{2}
\end{align*}
\sankaku{ACF}&=\dfrac{1}{2}\text{AF}\Cdota\text{CF}\sin\theta \\[4pt]
&=\dfrac{1}{2}\Cdota2\sqrt{5}\Cdota\dfrac{\sqrt{11}}{2\sqrt{5}} \\[4pt]
&=\dfrac{\sqrt{11}}{2}
\end{align*}
四面体と三角比

ヒロ
四面体に関する問題が東京慈恵会医科大で出題されている。
2015年 東京慈恵会医科大四面体ABCDにおいて,$\text{AB}=3$, $\text{BC}=\sqrt{13}$, $\text{CA}=4$, $\text{DA}=\text{DB}=\text{DC}=3$ とし,頂点Dから $\sankaku{ABC}$ に垂線DHを下ろす。このとき,DHの長さは $\myhako$,四面体ABCDの体積は $\myhako$ である。
【考え方と解答】
与えられた辺の長さを参考にして,適当な図を描こう。
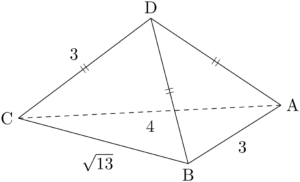
点Hが $\sankaku{ABC}$ のどの位置にくるかがすぐに分かる人は時間的に有利だろう。すぐに分からない場合は,丁寧に考えていこう。
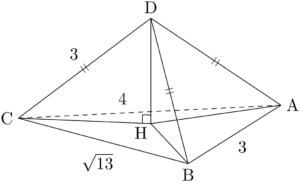
DHを含む三角形に着目することを考えると,$\sankaku{DHA}$, $\sankaku{DHB}$, $\sankaku{DHC}$ の3つがある。
これら3つの直角三角形は斜辺と1つの辺の長さがそれぞれ等しいから合同である。したがって,$\text{AH}=\text{BH}=\text{CH}$ となる。すなわち,点Hは $\sankaku{ABC}$ の外心である。つまり,AHの長さは $\sankaku{ABC}$ の外接円の半径に等しい。
$\sankaku{ABC}$ の3辺の長さが分かっているから,1つの内角に着目して余弦定理でコサイン,相互関係でサインを求めて,正弦定理で外接円の半径AHを求めよう。
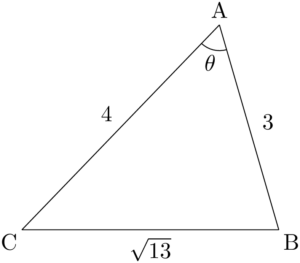
$\kaku{BAC}=\theta$ とすると,余弦定理より
正弦定理より
与えられた辺の長さを参考にして,適当な図を描こう。

点Hが $\sankaku{ABC}$ のどの位置にくるかがすぐに分かる人は時間的に有利だろう。すぐに分からない場合は,丁寧に考えていこう。

DHを含む三角形に着目することを考えると,$\sankaku{DHA}$, $\sankaku{DHB}$, $\sankaku{DHC}$ の3つがある。
これら3つの直角三角形は斜辺と1つの辺の長さがそれぞれ等しいから合同である。したがって,$\text{AH}=\text{BH}=\text{CH}$ となる。すなわち,点Hは $\sankaku{ABC}$ の外心である。つまり,AHの長さは $\sankaku{ABC}$ の外接円の半径に等しい。
$\sankaku{ABC}$ の3辺の長さが分かっているから,1つの内角に着目して余弦定理でコサイン,相互関係でサインを求めて,正弦定理で外接円の半径AHを求めよう。

$\kaku{BAC}=\theta$ とすると,余弦定理より
\begin{align*}
\cos\theta&=\dfrac{4^2+3^2-(\sqrt{13})^2}{2\Cdot4\Cdot3} \\[4pt]&=\dfrac{12}{2\Cdot4\Cdot3}=\dfrac{1}{2}
\end{align*}
よって $\theta=60\Deg$ であるから,$\sin\theta=\dfrac{\sqrt{3}}{2}$\cos\theta&=\dfrac{4^2+3^2-(\sqrt{13})^2}{2\Cdot4\Cdot3} \\[4pt]&=\dfrac{12}{2\Cdot4\Cdot3}=\dfrac{1}{2}
\end{align*}
正弦定理より
\begin{align*}
\text{AH}&=\dfrac{\text{BC}}{2\sin\theta} \\[4pt]&=\dfrac{\sqrt{13}}{\sqrt{3}}
\end{align*}
$\sankaku{AHC}$ において,三平方の定理より\text{AH}&=\dfrac{\text{BC}}{2\sin\theta} \\[4pt]&=\dfrac{\sqrt{13}}{\sqrt{3}}
\end{align*}
\begin{align*}
\text{DH}&=\sqrt{\text{DA}^2-\text{AH}^2} \\[4pt]&=\sqrt{3^2-\left(\dfrac{\sqrt{13}}{\sqrt{3}}\right)^2} \\[4pt]&=\sqrt{\dfrac{14}{3}}=\dfrac{\sqrt{42}}{3}
\end{align*}
次に四面体ABCDの体積を求めよう。底面を $\sankaku{ABC}$ にすると,DHが四面体の高さとなる。\text{DH}&=\sqrt{\text{DA}^2-\text{AH}^2} \\[4pt]&=\sqrt{3^2-\left(\dfrac{\sqrt{13}}{\sqrt{3}}\right)^2} \\[4pt]&=\sqrt{\dfrac{14}{3}}=\dfrac{\sqrt{42}}{3}
\end{align*}
\begin{align*}
\sankaku{ABC}&=\dfrac{1}{2}\Cdota4\Cdota3\Cdota\dfrac{\sqrt{3}}{2} \\[4pt]&=3\sqrt{3}
\end{align*}
であるから,求める体積を $V$ とすると\sankaku{ABC}&=\dfrac{1}{2}\Cdota4\Cdota3\Cdota\dfrac{\sqrt{3}}{2} \\[4pt]&=3\sqrt{3}
\end{align*}
\begin{align*}
V&=\dfrac{1}{3}\sankaku{ABC}\Cdota\text{DH} \\[4pt]&=\dfrac{1}{3}\Cdota3\sqrt{3}\Cdota\sqrt{\dfrac{14}{3}} \\[4pt]&=\sqrt{14}
\end{align*}
V&=\dfrac{1}{3}\sankaku{ABC}\Cdota\text{DH} \\[4pt]&=\dfrac{1}{3}\Cdota3\sqrt{3}\Cdota\sqrt{\dfrac{14}{3}} \\[4pt]&=\sqrt{14}
\end{align*}