大学入試では「○○を展開せよ」という問題が出題されることは少ないです。
しかし展開は数学の基礎であるため,大学入試で出題される場合は,展開を正しく理解しているかどうかが試されます。
ほとんどの場合は,特定の項の係数を求める問題として出題されます。
その際に利用することが多いのは二項定理ですが,今回は展開しても係数を求めることができるような簡単な問題を扱います。
Contents
定期テストで出題された問題

ヒロ
それでは次の問題を解いてみよう。
$xyz$ の係数を求める問題次の式を展開したときの $xyz$ の係数を答えよ。答えのみでよい。
\begin{align*}(2x+3y+z)(x+2y+3z)(3x+y+2z)\end{align*}
係数を求める問題の考え方と解答

ヒロ
求めたいものは $xyz$ の係数だから,全部を展開する必要はないね。

ヒロ
$xyz$ が現れる項だけを取り出そう。
展開複数の多項式 $A,~B$ の積 $AB$ を展開する場合,$A$,$B$ それぞれから1つの項を選んでそれらの積を1つの項とする。すべての組み合わせで求めた項の和が $AB$ の展開式となる。

ヒロ
今回の場合は3つの括弧があるため,それぞれの括弧から $x,~y,~z$ の項を1つずつ選んだ項の積の和を考えれば良いね。
【解答】
答えを求めれば良い問題なので,$xyz$ の係数を求めやすくなるように,それぞれの項の係数を工夫して書いて求めることにする。$x,~y,~z$ の係数を左から順に並べて,括弧ごとに縦に並べて書くと次のようになる。

同じ行と列から2つ以上の数字を選ばないように3つの数字を選ぶと次のように機械的に数字を選ぶことができる。
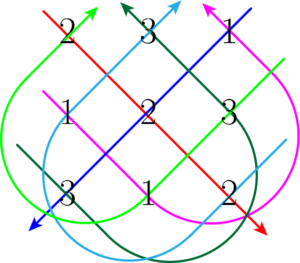
求める係数は,選んだ3つの数の積の和がだから
答えを求めれば良い問題なので,$xyz$ の係数を求めやすくなるように,それぞれの項の係数を工夫して書いて求めることにする。$x,~y,~z$ の係数を左から順に並べて,括弧ごとに縦に並べて書くと次のようになる。

同じ行と列から2つ以上の数字を選ばないように3つの数字を選ぶと次のように機械的に数字を選ぶことができる。

求める係数は,選んだ3つの数の積の和がだから
\begin{align*}
&{\color[named]{Red}2\Cdota2\Cdota2}+{\color[named]{Lavender}1\Cdota1\Cdota1}+{\color[named]{OliveGreen}3\Cdota3\Cdota3}
+{\color[named]{Blue}1\Cdota2\Cdota3}+{\color[named]{LimeGreen}3\Cdota1\Cdota2}+{\color[named]{Cyan}2\Cdota1\Cdota3} \\[4pt]
&=8+1+27+6+6+6 \\[4pt]
&=54
\end{align*}
※数字の色は対応する矢印の類似色&{\color[named]{Red}2\Cdota2\Cdota2}+{\color[named]{Lavender}1\Cdota1\Cdota1}+{\color[named]{OliveGreen}3\Cdota3\Cdota3}
+{\color[named]{Blue}1\Cdota2\Cdota3}+{\color[named]{LimeGreen}3\Cdota1\Cdota2}+{\color[named]{Cyan}2\Cdota1\Cdota3} \\[4pt]
&=8+1+27+6+6+6 \\[4pt]
&=54
\end{align*}
2012年 自治医科大

ヒロ
次の問題を解いてみよう。
2012年 自治医科大
\begin{align*} (a^3+4a^2b-ab^2+3b^3)(-a^4+2a^3b+3a^2b^2+b^4) \end{align*}
を展開するとき,$a^4b^3$ の係数の値を求めよ。2012年 自治医科大の考え方と解答

ヒロ
これは左の括弧から1つ項を選んだとき,もう1つの括弧から項を1つ選んで $a^4b^3$ の項になるものを探すだけだね。
【解答】
$a^4b^3$ の同類項をぬき出すと,
$a^4b^3$ の同類項をぬき出すと,
\begin{align*}
4a^2b\Cdota3a^2b^2-ab^2\Cdota2a^3b+3b^3\Cdota(-a^4)=7a^4b^3
\end{align*}
となるから,求める係数は7である。4a^2b\Cdota3a^2b^2-ab^2\Cdota2a^3b+3b^3\Cdota(-a^4)=7a^4b^3
\end{align*}
2011年 金沢工業大

ヒロ
次の問題を解いてみよう。
2011年 金沢工業大$(2a+1)(2a-1)(a^2-a+4)$ の展開式における $a^2$ の係数は $\myhako$ である。
2011年 金沢工業大の考え方と解答

これはそのまま展開しても求められますね。

ヒロ
そうだけど,簡単な問題だからこそ,特定の項だけを取り出す練習をするべきだね。

ヒロ
ただし今回は最初の2つの括弧だけは展開した方が考えやすいね。
【解答】
\begin{align*}
&(2a+1)(2a-1)(a^2-a+4) \\[4pt]&=(4a^2-1)(a^2-a+4)
\end{align*}
となるから,求める $a^2$ の係数は&(2a+1)(2a-1)(a^2-a+4) \\[4pt]&=(4a^2-1)(a^2-a+4)
\end{align*}
\begin{align*}
4\Cdota4-1\Cdota1=15
\end{align*}
4\Cdota4-1\Cdota1=15
\end{align*}



















