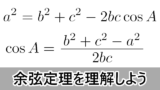ここでは三角形の角の大きさと辺の長さの関係について説明します。
三角形の形状を大雑把に分類すると次の3つに分けられます。
- 鋭角三角形
- 直角三角形
- 鈍角三角形
三平方の定理が成り立つときは直角三角形だと分かります。
直角三角形でない場合は,鋭角三角形か鈍角三角形になります。
三平方の定理の一般形ともいえる余弦定理で判断できるようにしましょう。
余弦定理については次の記事で復習しておこう。
三角形の角の大きさと辺の長さの関係

ヒロ
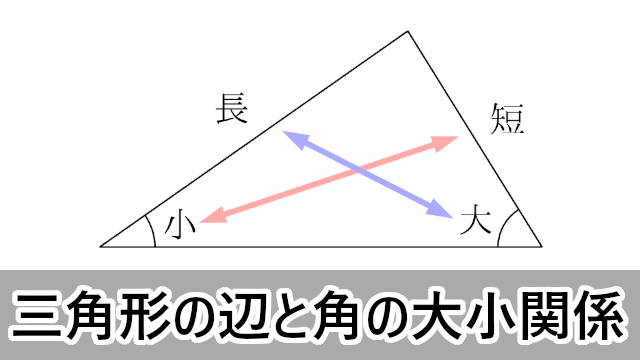
三角形について,次のことが成り立つことが知られている。
三角形の角と辺三角形の2辺の大小関係は,その向かい合う角の大小関係と一致する。
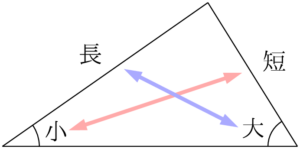
もう少し細かく言うと次のようになる。
① 大きい辺に向かい合う角は,小さい辺に向かい合う角より大きい。
② 大きい角に向かい合う辺は,小さい角に向かい合う辺より大きい。

もう少し細かく言うと次のようになる。
① 大きい辺に向かい合う角は,小さい辺に向かい合う角より大きい。
② 大きい角に向かい合う辺は,小さい角に向かい合う辺より大きい。

ヒロ
当たり前のことかもしれないが,念のため証明しておこう。

ヒロ
そのための準備として次のことを知っておこう。
【角の大きさに関する知識】
次のような直線ABと直線AB上にない点Pと直線AB上の点Qを考える。
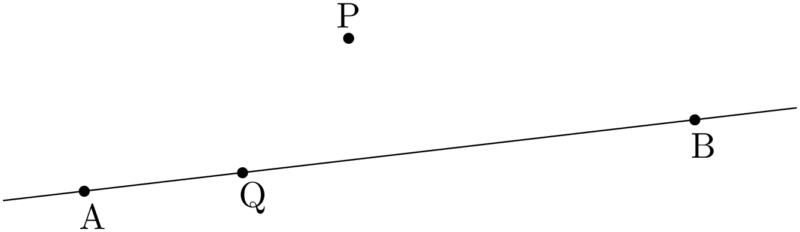
直線AB上に点Qをとり,$\kaku{PQB}$ を考える。点Pから直線ABに下ろした垂線の足をHとすると,HよりA側に点Qがあるとき,$\kaku{PQB}$ は鋭角になり,線分BH上に点Qがあるときは $\kaku{PQB}$ は鈍角になる。
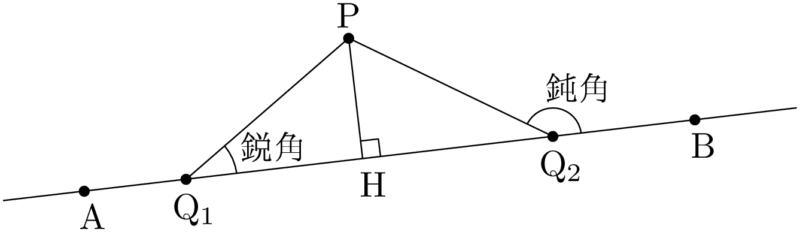
この結果から,点QをAからBの方へ動かすにつれて,$\kaku{PQB}$ は大きくなることが分かる。
次のような直線ABと直線AB上にない点Pと直線AB上の点Qを考える。

直線AB上に点Qをとり,$\kaku{PQB}$ を考える。点Pから直線ABに下ろした垂線の足をHとすると,HよりA側に点Qがあるとき,$\kaku{PQB}$ は鋭角になり,線分BH上に点Qがあるときは $\kaku{PQB}$ は鈍角になる。

この結果から,点QをAからBの方へ動かすにつれて,$\kaku{PQB}$ は大きくなることが分かる。

ヒロ
それでは,三角形の2辺の大小関係は,その向かい合う角の大小関係と一致することを証明しよう。
【証明】
まず,$\text{AC}>\text{BC}$ である $\sankaku{ABC}$ について,$A<B$ であることを証明する。
$\text{BC}=\text{CD}$ となるように辺AC上に点Dをとると,$\sankaku{BCD}$ は二等辺三角形であるから,$\kaku{CDB}=\kaku{CBD}$ となる。
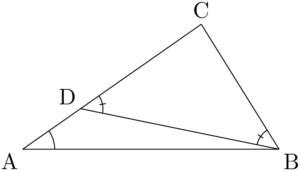
ここで $\kaku{BAC}<\kaku{BDC}$ であるから,$\kaku{BAC}<\kaku{CBD}$,すなわち $A<B$ である。 逆に $A<B$ のときも同様に考えれば $\text{AC}>\text{BC}$ であることは明らかである。
したがって,三角形の2辺の大小関係は,その向かい合う角の大小関係と一致する。
まず,$\text{AC}>\text{BC}$ である $\sankaku{ABC}$ について,$A<B$ であることを証明する。
$\text{BC}=\text{CD}$ となるように辺AC上に点Dをとると,$\sankaku{BCD}$ は二等辺三角形であるから,$\kaku{CDB}=\kaku{CBD}$ となる。

ここで $\kaku{BAC}<\kaku{BDC}$ であるから,$\kaku{BAC}<\kaku{CBD}$,すなわち $A<B$ である。 逆に $A<B$ のときも同様に考えれば $\text{AC}>\text{BC}$ であることは明らかである。
したがって,三角形の2辺の大小関係は,その向かい合う角の大小関係と一致する。
三角形の形状を調べる方法

ヒロ
それでは,直角三角形・鋭角三角形・鈍角三角形のいずれであるかを調べる方法を説明する。

ヒロ
三角形の内角の和は180°であるから,三角形の最大角以外の角はすべて鋭角である。
三角形の最大角三角形の3つの辺のうち,最も長い辺の対角が最大角であり,それ以外の2つの角は必ず鋭角である。

ヒロ
つまり,三角形が鋭角三角形,直角三角形,鈍角三角形のいずれであるかは,最大角によって決まる。

ヒロ
三角形の辺と角の大小関係が一致するから,最大辺の対角に着目して考えよう。
【三角形の形状を調べる方法】
三角形の内角の1つに着目したとき,その角が鋭角・直角・鈍角かを調べるには,その角のコサインの符号を調べれば良い。例えば $A$ を調べるときは,余弦定理を利用して
三角形の内角の1つに着目したとき,その角が鋭角・直角・鈍角かを調べるには,その角のコサインの符号を調べれば良い。例えば $A$ を調べるときは,余弦定理を利用して
\begin{align*}
\cos A=\dfrac{b^2+c^2-a^2}{2bc}
\end{align*}
の符号を調べれば良い。ここで,分母の $2bc$ は常に正であるから,$\cos A$ の符号と $b^2+c^2-a^2$ の符号は一致する。つまり,$b^2+c^2-a^2$ の符号を調べれば良いことになる。ちなみにこれは $a^2$ と $b^2+c^2$ の大小関係を調べることと同じである。\cos A=\dfrac{b^2+c^2-a^2}{2bc}
\end{align*}

ヒロ
まとめると次のようになる。
三角形ABCの形状
- $a^2<b^2+c^2$ のとき,鋭角三角形
-
$a^2=b^2+c^2$ のとき,直角三角形
- $a^2>b^2+c^2$ のとき,鈍角三角形
三角形の形状を調べる問題

ヒロ
それでは,直角三角形・鋭角三角形・鈍角三角形のいずれであるかを調べる問題を解いてみよう。
問題$\sankaku{ABC}$ において,3辺の長さが次のようなとき,$\sankaku{ABC}$ は鋭角三角形,直角三角形,鈍角三角形のいずれであるか。
(1) $a=4,~b=3,~c=2$
(2) $a=5,~b=6,~c=7$
(3) $a=12,~b=13,~c=5$
(1) $a=4,~b=3,~c=2$
(2) $a=5,~b=6,~c=7$
(3) $a=12,~b=13,~c=5$
【(1)の考え方と解答】
最大辺の長さが $a=4$ であるから,$a^2$ と $b^2+c^2$ の大小関係を調べる。
よって,$\sankaku{ABC}$ は鈍角三角形である。
最大辺の長さが $a=4$ であるから,$a^2$ と $b^2+c^2$ の大小関係を調べる。
\begin{align*}
&a^2=4^2=16 \\[4pt]&b^2+c^2=3^2+2^2=13
\end{align*}
となるから,$a^2>b^2+c^2$ である。&a^2=4^2=16 \\[4pt]&b^2+c^2=3^2+2^2=13
\end{align*}
よって,$\sankaku{ABC}$ は鈍角三角形である。
(2) $a=5,~b=6,~c=7$
【(2)の考え方と解答】
最大辺の長さが $ac=7$ であるから,$c^2$ と $a^2+b^2$ の大小関係を調べる。
よって,$\sankaku{ABC}$ は鋭角三角形である。
最大辺の長さが $ac=7$ であるから,$c^2$ と $a^2+b^2$ の大小関係を調べる。
\begin{align*}
&c^2=7^2=49 \\[4pt]&a^2+b^2=5^2+6^2=61
\end{align*}
となるから,$c^2<a^2+b^2$ である。&c^2=7^2=49 \\[4pt]&a^2+b^2=5^2+6^2=61
\end{align*}
よって,$\sankaku{ABC}$ は鋭角三角形である。
(3) $a=12,~b=13,~c=5$
【(3)の考え方と解答】
最大辺の長さが $b=13$ であるから,$b^2$ と $c^2+a^2$ の大小関係を調べる。
よって,$\sankaku{ABC}$ は直角三角形である。
最大辺の長さが $b=13$ であるから,$b^2$ と $c^2+a^2$ の大小関係を調べる。
\begin{align*} &b^2=13^2=169 \\[4pt] &c^2+a^2=12^2+5^2=169 \end{align*}
となるから,$b^2=c^2+a^2$ である。よって,$\sankaku{ABC}$ は直角三角形である。

ヒロ
3辺が整数の直角三角形として,$3:4:5$ の直角三角形と $5:12:13$ の直角三角形の2つは常識にしておきたい。

ヒロ
覚えている人は $8:15:17$ や $7:24:25$ の直角三角形も覚えている。

ヒロ
「見た瞬間に分かる」というのは意外と重要である。