外積を利用した2つのベクトルに垂直なベクトルの求め方とは？

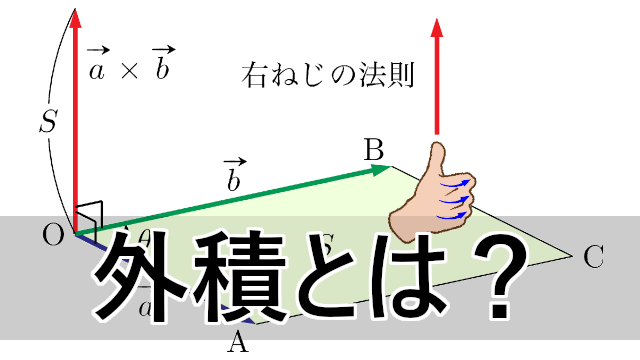
ここでは外積について説明します。外積は2つのベクトルに垂直なベクトルを求める方法に活用できます。また，外積のもつ性質と内積の図形的意味を利用することで，四面体の体積を求める公式まで簡単に導出できます。外積を使いこなせるようにしましょう！

そもそもベクトルが苦手な人は，「細野真宏のベクトル〈平面図形〉が本当によくわかる本」のような解説がしっかり書かれている参考書で，基礎を身に付けた方が，結果として，早く成績を上げることができるでしょう。中身を立ち読みできるので，数ページ読めば，解説がどんな感じか分かると思います。

細野真宏のベクトル〈平面図形〉が本当によくわかる本　数B

トップカルチャーnetクラブ

Amazon

楽天

Yahoo!ショッピング

Contents

1つのベクトルの成分に0がある場合

2018年産業医科大座標空間において，3点 $\mathrm{A}(1,1,2)$，$\mathrm{B}(0,1,4)$，$\mathrm{C}(1,-2,-1)$ を通る平面と
点 $\mathrm{D}(1,1,1)$ の距離は $\myhako$ である。

プリントを次のリンクからダウンロードできます。

ダウンロード

ヒロ

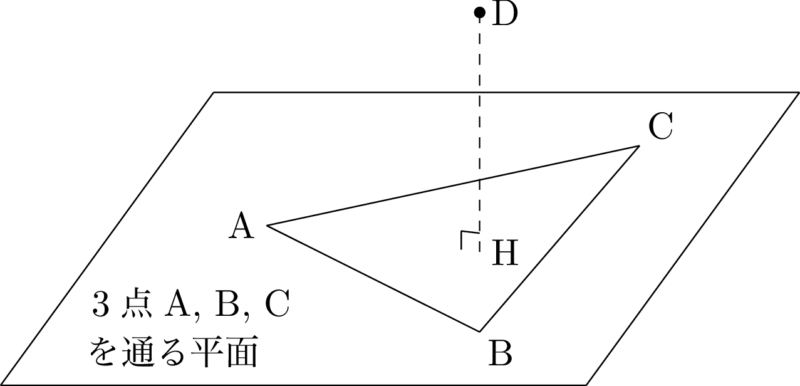
まずは簡単な図を描こう。その際に，点Dから平面ABC（3点A，B，Cを通る平面）に下ろした垂線の足をHとすると，求めたいのはDHの距離だと分かるね。

そうですね。でも空間座標を見ると，つい細かく図を描いてしまうんですよね・・・

ヒロ

図を描くのに時間をかけるのは得策と言えないかも。ササッと描いて，何をすれば良いかということを考えるのに時間を使おう。そして，空間座標ではベクトルで考えるのが基本ということも覚えておこう。

ヒロ

この問題ではDHの長さを求めたいので，これをベクトル $\left(\Vec{DH}\right.$ や $\left.\Vec{HD}\right)$ の大きさと捉えよう。

そのままですね・・・

ヒロ

ベクトルは方向と大きさの2つの情報をもってるものだよね。大きさを求めたいけど，それがすぐ求められるなら苦労しないわけで，まずはもう1つの要素である方向を考えよう。

方向は平面ABCに垂直な方向ですよね？

ヒロ

そうだけど，それを言い換えよう。つまり，$\Vec{DH}$ の方向は $\Vec{AB}$ と $\Vec{AC}$ の両方に垂直な方向だと言えるよね？

そうですね。

直線 $\ell$ と平面 $\alpha$ が垂直であるとき，直線 $\ell$ は平面 $\alpha$ 上の任意の直線と垂直である。

ヒロ

いま，$\Vec{AB}$ と $\Vec{AC}$ の両方に垂直な単位ベクトルを $\vec{n}$ として図を描くとこうなるね。

ヒロ

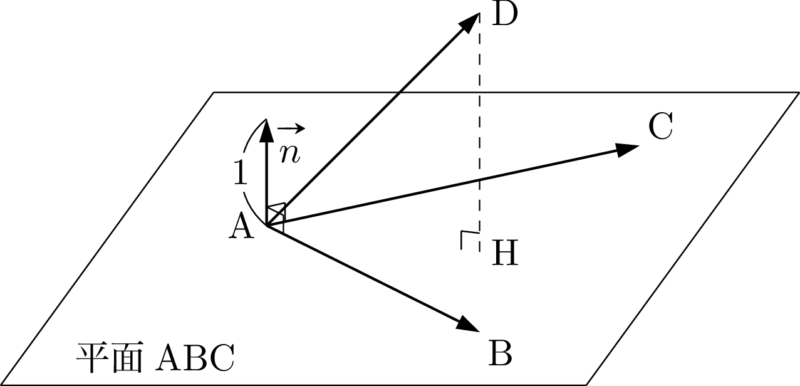
さらに，この状態を平面ABCが直線に見える方向から見た図を考えよう。

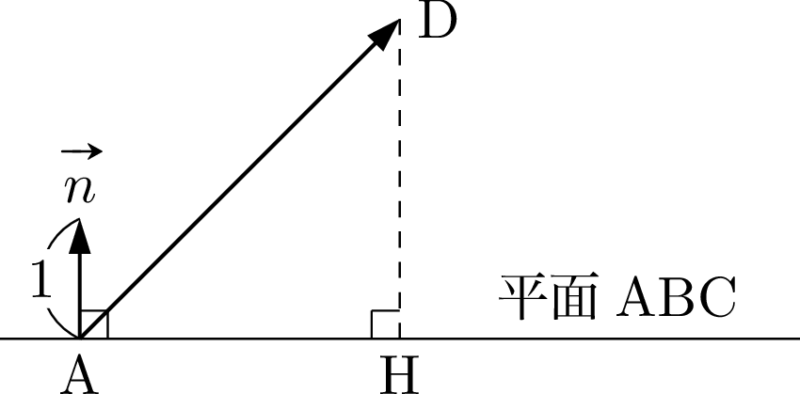
あれ・・・？これって内積の図形的意味を考えればDHの長さを求められるんじゃないんですか？

ベクトルの内積の図形的意味とは？

ベクトルの内積の図形的意味を理解することで，点と直線の距離の公式の証明を簡単にすることができます。また，正射影ベクトルについても理解できるため，様々な問題でも柔軟に考えることが出来るようになります。

ヒロ

そうだね。ということはDHはどうなるの？

$\mathrm{DH}=\abs{\vec{n}\Cdot\Vec{AD}}$ ですね！

ヒロ

これで方針は決まったね。ということで，$\vec{n}$ の成分を求めよう。

はい！

$\Vec{AB}$ と $\Vec{AC}$ の両方に垂直な単位ベクトルを $\vec{n}=(x,y,z)$ とおくと，

\begin{align*}
|\vec{n}|=1,~\Vec{AB}\Cdota\vec{n}=0,~\Vec{AC}\Cdota\vec{n}=0
\end{align*}

が成り立つ。また，

\begin{align*}
\Vec{AB}=(-1,0,2),~\Vec{AC}=(0,-3,-3)
\end{align*}

であるから

\begin{align*}
\begin{cases}
x^2+y^2+z^2=1 & \cdots\cdots① \\[4pt]
-x+2z=0 & \cdots\cdots② \\[4pt]
-3y-3z=0 & \cdots\cdots③
\end{cases}
\end{align*}

②より，$x=2z$ であり，③より，$y=-z$ であるから，①に代入して

\begin{align*}
&(2z)^2+(-z)^2+z^2=1 \\[4pt]
&6z^2=1 \\[4pt]
&z=\pm\dfrac{1}{\sqrt{6}}
\end{align*}

よって，$\vec{n}=\pm\dfrac{1}{\sqrt{6}}(2,-1,1)$

求まりました！

ヒロ

毎回この方法でやってるの？

この方法しか知りません・・・

ヒロ

この問題だと暗算で求められるんだけど・・・

えっ？そうなんですか！

ヒロ

ただし，$\Vec{AB}$ と $\Vec{AC}$ のどちらかの成分に0が含まれているときしか使えないけどね。

ヒロ

とりあえず，$\Vec{AB}$ の成分 $(-1,0,2)$ に着目しよう。$y$ 成分が0だから，$x$ 成分と $z$ 成分を見て，内積が0になるように $\vec{n}$ の成分を決めよう。$\vec{n}=(2,\heartsuit,1)$ とすれば，$\heartsuit$ がどんな数でも $\Vec{AB}\Cdot\vec{n}=0$ が成り立つよね。

そうですね。$\Vec{AB}$ の $y$ 成分が0だから，$\vec{n}$ の $y$ 成分は何でも良いんですね。

ヒロ

次に，$\heartsuit$ を決めるために，$\Vec{AC}=(0,-3,-3)$ との内積を考えよう。$\Vec{AC}$ と平行なベクトル $(0,1,1)$ との内積を考えても良いけど，今回はそのままやっとくよ。

\begin{align*}
&\Vec{AC}\Cdota\vec{n}=-3\times\heartsuit-3=0 \\[4pt]
&\heartsuit=-1
\end{align*}

ヒロ

これで $\vec{n}=(2,-1,1)$ となったけど，これは単位ベクトルかどうかは分からないよね。というか，適当に求めて大きさが1になってたら，逆にすごいよね。

ヒロ

だから，これを単位ベクトルにするために，$\abs{\vec{n}}$ を求めよう。

$\abs{\vec{n}}=\sqrt{2^2+(-1)^2+1^2}=\sqrt{6}$ です。

ヒロ

そうだね。ということで，求めたい単位ベクトル $\vec{n}$ は $\vec{n}=\dfrac{1}{\sqrt{6}}(2,-1,1)$ ってことだね。

あとはベクトルの内積の図形的意味を使って終わりですね！

$\Vec{AD}=(0,0,-1)$ であるから，

\begin{align*}
\mathrm{DH}&=\abs{\vec{n}\Cdota\Vec{AD}} \\[4pt]
&=\abs{\dfrac{1}{\sqrt{6}}(2,-1,1)\Cdota(0,0,-1)} \\[4pt]
&=\abs{-\dfrac{1}{\sqrt{6}}} \\[4pt]
&=\dfrac{\sqrt{6}}{6}
\end{align*}

できました！楽ですね。