Contents
- ページ1
- 1 1つのベクトルの成分に0がある場合
- ページ2
- 1 垂線の足の座標
- ページ3
- 1 1つのベクトルの成分に0がない場合
- ページ4
- 1 外積の性質
- ページ5
- 1 四面体の体積
- 2 まとめ
四面体の体積

総仕上げとして,次の四面体ABCDの体積 $V$ を求めてみよう。
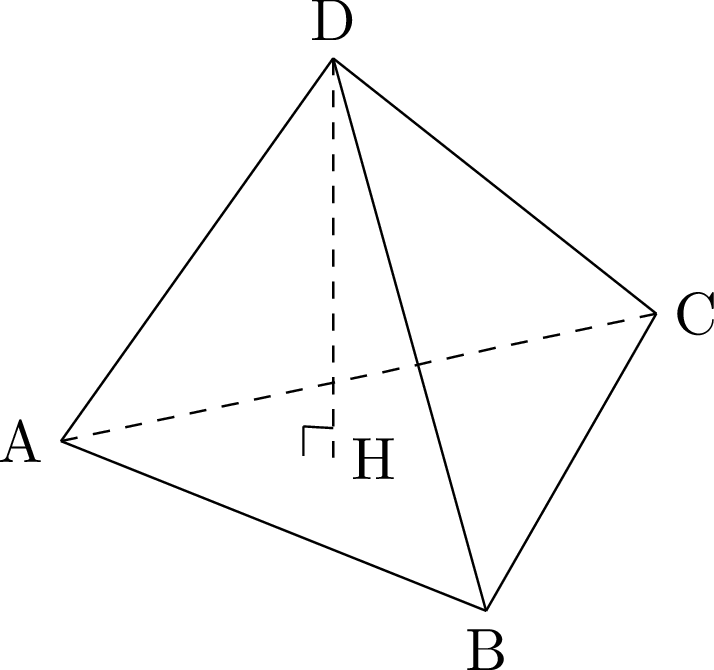

まず,$V$ を $\triangle\mathrm{ABC}$ とDHを用いて表すとどうなる?

$V=\dfrac{1}{3}\Cdot\triangle\mathrm{ABC}\Cdot\mathrm{DH}$ です。

そうだね。次にDHの長さをベクトルで表すために $\Vec{AB}\times\Vec{AC}$ を考えよう。
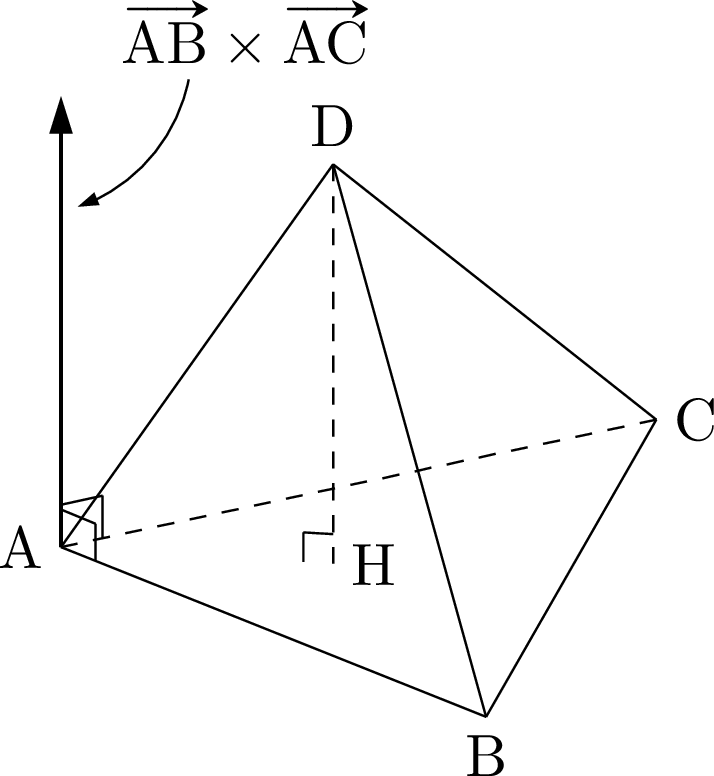

$\Vec{AD}$ との内積を考えて,こうですね!
\begin{align*}
\left(\Vec{AB}\times\Vec{AC}\right)\Cdota\Vec{AD}=\abs{\Vec{AB}\times\Vec{AC}}\Cdota\mathrm{DH}
\end{align*}

外積の大きさはそれを作る2つのベクトルで作られる平行四辺形の面積に等しいことを考えると四面体の体積はどうなる?
$\abs{\Vec{AB}\times\Vec{AC}}=2\triangle\mathrm{ABC}$より,
\begin{align*}
\triangle\mathrm{ABC}=\dfrac{1}{2}\abs{\Vec{AB}\times\Vec{AC}}
\end{align*}であるから
\begin{align*}
V&=\dfrac{1}{3}\Cdota\dfrac{1}{2}\abs{\Vec{AB}\times\Vec{AC}}\Cdota\mathrm{DH} \\
&=\dfrac{1}{6}\left(\Vec{AB}\times\Vec{AC}\right)\Cdota\Vec{AD}
\end{align*}

四面体の4点の座標が与えられていれば,四面体の体積は結構簡単に求められるんですね。

まとめ

外積を使いこなすことで有利になるのは間違いなし!
外積の5つのポイント
- 外積は「$\times$」を使って表す。
- $\vec{a}\times\vec{b}$ は $\vec{a}$ と $\vec{b}$ の両方に垂直なベクトル。
- 方向は $\vec{a}$ から $\vec{b}$ の方向に右ねじを回すときに,ねじが進む方向。
- $|\vec{a}\times\vec{b}|$ は $\vec{a}$ と $\vec{b}$ で作られる平行四辺形の面積と等しい。
- 順序を変えると符号が変わる。$\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$

平面ベクトルは大丈夫だけど,空間ベクトルになるとサッパリ出来ないという人は,細野真宏さんの本がオススメ。

最初に紹介した平面ベクトルの本と同様,かなり詳しく書かれている。平面ベクトルの本がセクション3で終わっていて,空間ベクトルはその続編という扱い。そのため,セクション4から始まる構成になっている。

ベクトル自体が苦手なら,平面と空間の2冊を買うのが手っ取り速いかもしれない。

ヒロ
総仕上げとして,次の四面体ABCDの体積 $V$ を求めてみよう。


ヒロ
まず,$V$ を $\triangle\mathrm{ABC}$ とDHを用いて表すとどうなる?

$V=\dfrac{1}{3}\Cdot\triangle\mathrm{ABC}\Cdot\mathrm{DH}$ です。

ヒロ
そうだね。次にDHの長さをベクトルで表すために $\Vec{AB}\times\Vec{AC}$ を考えよう。


$\Vec{AD}$ との内積を考えて,こうですね!
\begin{align*}
\left(\Vec{AB}\times\Vec{AC}\right)\Cdota\Vec{AD}=\abs{\Vec{AB}\times\Vec{AC}}\Cdota\mathrm{DH}
\end{align*}
\left(\Vec{AB}\times\Vec{AC}\right)\Cdota\Vec{AD}=\abs{\Vec{AB}\times\Vec{AC}}\Cdota\mathrm{DH}
\end{align*}

ヒロ
外積の大きさはそれを作る2つのベクトルで作られる平行四辺形の面積に等しいことを考えると四面体の体積はどうなる?
\begin{align*}
\triangle\mathrm{ABC}=\dfrac{1}{2}\abs{\Vec{AB}\times\Vec{AC}}
\end{align*}
であるから\triangle\mathrm{ABC}=\dfrac{1}{2}\abs{\Vec{AB}\times\Vec{AC}}
\end{align*}
\begin{align*}
V&=\dfrac{1}{3}\Cdota\dfrac{1}{2}\abs{\Vec{AB}\times\Vec{AC}}\Cdota\mathrm{DH} \\
&=\dfrac{1}{6}\left(\Vec{AB}\times\Vec{AC}\right)\Cdota\Vec{AD}
\end{align*}
V&=\dfrac{1}{3}\Cdota\dfrac{1}{2}\abs{\Vec{AB}\times\Vec{AC}}\Cdota\mathrm{DH} \\
&=\dfrac{1}{6}\left(\Vec{AB}\times\Vec{AC}\right)\Cdota\Vec{AD}
\end{align*}

四面体の4点の座標が与えられていれば,四面体の体積は結構簡単に求められるんですね。

4点の座標が与えられたときの四面体の体積の求め方とは?
四面体の4点の座標が与えられたとき,外積を利用することで簡単に四面体の体積を求めることができます。また,外積を書かなくても良い解答の書き方を知ることで減点されるかなどの心配もなくなります。これからは楽に四面体の体積を求めましょう。

【ベクトルの勉強法】1か月でベクトルの応用レベルの問題を解けるようにする方法
1か月でベクトルができるようになる勉強法を説明します。得意になることが確定していて,その方法も分かっているのに行動しない人が多いです。つまり,行動を始めるだけで,ライバルに勝てるということです。今すぐ行動し始めてベクトルを得意にしましょう。

ヒロ
外積を使いこなすことで有利になるのは間違いなし!
外積の5つのポイント
- 外積は「$\times$」を使って表す。
- $\vec{a}\times\vec{b}$ は $\vec{a}$ と $\vec{b}$ の両方に垂直なベクトル。
- 方向は $\vec{a}$ から $\vec{b}$ の方向に右ねじを回すときに,ねじが進む方向。
- $|\vec{a}\times\vec{b}|$ は $\vec{a}$ と $\vec{b}$ で作られる平行四辺形の面積と等しい。
- 順序を変えると符号が変わる。$\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$

ヒロ
平面ベクトルは大丈夫だけど,空間ベクトルになるとサッパリ出来ないという人は,細野真宏さんの本がオススメ。

ヒロ
最初に紹介した平面ベクトルの本と同様,かなり詳しく書かれている。平面ベクトルの本がセクション3で終わっていて,空間ベクトルはその続編という扱い。そのため,セクション4から始まる構成になっている。

ヒロ
ベクトル自体が苦手なら,平面と空間の2冊を買うのが手っ取り速いかもしれない。


















![細野真宏のベクトル[平面図形]が本当によくわかる本【電子書籍】[ 細野真宏 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/1079/2000003771079.jpg?_ex=128x128)
