2つの円柱の共通部分の体積を求める問題と3つの円柱の共通部分の体積を求める問題を説明します。
2つの円柱の共通部分がどのような立体になっているかが想像できなくても,その体積を求めることはできます。
数学が苦手な人は図を描くことができないから解けないと思っていますが,根本的に間違っています。
実際のところ,図を描く能力は別のスキルであり,数学力と関係ありません。
また図を描くことができたとしても,結局,その立体の体積を求めることができなければ図を描くだけ無駄だったということにもなります。
そうならないためにも正しい考え方を身に付けて解ける問題を増やしましょう。
Contents
2004年 名古屋市立大・医

それでは次の問題を解いてみよう。
(1) 座標空間の平面 $z=t~(-1\leqq t\leqq1)$ 上で $x$ 軸,$y$ 軸までの距離がいずれも1以下である領域の面積を求めよ。
(2) 座標空間において,$x$ 軸,$y$ 軸までの距離がいずれも1以下である部分の体積を求めよ。
(3) 座標空間において,$x$ 軸,$y$ 軸,$z$ 軸までの距離がいずれも1以下である部分の体積を求めよ。
(1)の考え方と解答【2円柱の共通部分の断面】

何がどうなっているかさっぱり分からないとき以外は「まずは図を描く」を辞めよう。

大体の様子を理解している状態で,どのように解くか分からないからという理由で図を描いたとしても,結局分からないということになる。

既に分かっていることを図に描いただけで,何も進んでいないのなら,図を描く時間が無駄な時間となる。

今回扱っている問題では,座標空間内の点 $(x,~y,~z)$ から $x$ 軸に下ろした垂線の足が $(x,~0,~0)$ となることを理解しよう。

これを理解することで,点 $(x,~y,~z)$ から $x$ 軸までの距離が $\sqrt{y^2+z^2}$ であることも理解できるはず。
平面 $z=t$ 上の点 $(x,~y,~t)$ から $x$ 軸までの距離は $\sqrt{y^2+t^2}$,$y$ 軸までの距離は $\sqrt{x^2+t^2}$ だから,$x$ 軸,$y$ 軸までの距離がいずれも1以下である領域は
&\sqrt{y^2+t^2}\leqq1~~かつ~~\sqrt{x^2+t^2}\leqq1 \\[4pt]
&\abs{x}\leqq\sqrt{1-t^2}~~かつ~~\abs{y}\leqq\sqrt{1-t^2}
\end{align*}
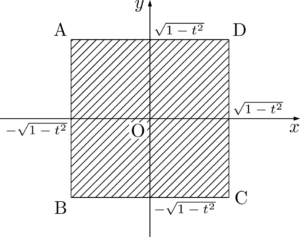
したがって,求める面積は
\left(2\sqrt{1-t^2}\right)^2=4(1-t^2)
\end{align*}
(2)の考え方と解答【2円柱の共通部分の体積】
(2) 座標空間において,$x$ 軸,$y$ 軸までの距離がいずれも1以下である部分の体積を求めよ。

平面 $z=t$ で切った切り口の面積が分かれば,所謂「薄切りハムの体積」が分かったようなものだから,立体全体の体積も計算できるね。
題意の部分を平面 $z=t$ で切った切り口の面積は(1)より $4(1-t^2)$ だから,求める体積は
\dint{-1}{1}4(1-t^2)\;dt&=8\dint{0}{1}(1-t^2)\;dt \\[4pt]
&=8\Tint{t-\dfrac13t^3}{0}{1} \\[4pt]&=\dfrac{16}{3}
\end{align*}
(3)の考え方と解答【3円柱の共通部分の体積】
(3) 座標空間において,$x$ 軸,$y$ 軸,$z$ 軸までの距離がいずれも1以下である部分の体積を求めよ。

最後は3つの円柱の共通部分の体積を求める問題。

まずは断面積を求めよう。

つまり(1)で図示した正方形とそれに直交する円柱との共通部分の面積を求めることを考える。

円が正方形の外側にはみ出るかどうかで場合分けが必要なことが分かるだろう。

具体的にはOAの長さ $\sqrt{2}\sqrt{1-t^2}$ と円柱の半径1との大小関係で場合分けをする。
$\sqrt{2}\sqrt{1-t^2}\leqq1$ のとき
&2(1-t^2)\leqq1 \\[4pt]
&1-t^2\leqq\dfrac{1}{2} \\[4pt]
&t^2\geqq\dfrac{1}{2}
\end{align*}
逆に $\sqrt{2}\sqrt{1-t^2}\geqq1$ のときは,円の一部が正方形からはみ出るため,共通部分の面積を求めるのは少し面倒。

解答は簡単に書くことができる方から書いていこう。
題意の部分を平面 $z=t$ で切った切り口の面積を $S(t)$ とする。
点 $(x,~y,~z)$ から $z$ 軸までの距離は $\sqrt{x^2+y^2}$ だから $S(t)$ は(1)の領域と円 $x^2+y^2=1$ との共通部分の面積である。
(i) $t^2\geqq\dfrac{1}{2}$ のとき
(1)の正方形ABCDは円$x^2+y^2=1$に含まれるから,
S(t)=4(1-t^2)
\end{align*}
$t=\sin\theta~\left(0\leqq\theta\leqq\dfrac{\pi}{4}\right)$ とすると,
$\sqrt{1-t^2}=\cos\theta$ となる。$S(t)$ は図の斜線部分の4倍である。
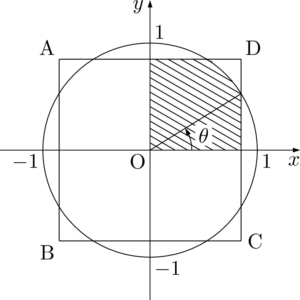
2つの直角三角形と1つの扇形に分割して面積を求めると次のようになる。
S(t)&=4\left\{\dfrac12\Cdota1^2\Cdota\left(\dfrac{\pi}{2}-2\theta\right)
+2\times\dfrac12\sin\theta\cos\theta\right\} \\[4pt]
&=\pi-4\theta+4\sin\theta\cos\theta
\end{align*}
\begin{array}{c|ccc}
t & 0 & \to & \dfrac{1}{\sqrt{2}} \\\hline
\theta & 0 & \to & \dfrac{\pi}{4}
\end{array},~~dt=\cos\theta d\theta
\end{align*}
V&=2\left\{\dint{\sqrt{\frac12}}{1}4(1-t^2)\;dt
+\dint{0}{\sqrt{\frac12}}S(t)\;dt\right\} \\[4pt]
&=2\left\{\dint{\sqrt{\frac12}}{1}4(1-t^2)\;dt
+\dint{0}{\frac{\pi}{4}}(\pi-4\theta+4\sin\theta\cos\theta)\cos\theta\;d\theta\right\}
\end{align*}
\dint{\sqrt{\frac12}}{1}4(1-t^2)\;dt
&=\Tint{4t-\dfrac43t^3}{\sqrt{\frac12}}{1} \\[4pt]
&=\left(4-\dfrac43\right)-\left(4\Cdota\dfrac{\sqrt2}{2}
-\dfrac43\Cdota\dfrac12\Cdota\dfrac{\sqrt2}{2}\right) \\[4pt]
&=\dfrac83-\dfrac{5\sqrt2}{3}
\end{align*}
&\dint{0}{\frac{\pi}{4}}(\pi-4\theta+4\sin\theta\cos\theta)\cos\theta\;d\theta \\[4pt]
=&\dint{0}{\frac{\pi}{4}}(\pi\cos\theta-4\theta\cos\theta
+4\sin\theta\cos^2\theta)\;d\theta \\[4pt]
=&\Tint{\pi\sin\theta
-4(\theta\sin\theta+\cos\theta)-\dfrac43\cos^3\theta}{0}{\frac{\pi}{4}} \\[4pt]
=&\dfrac{\sqrt2}{2}\pi-4\left(\dfrac{\pi}{4}\Cdota\dfrac{\sqrt2}{2}
+\dfrac{\sqrt2}{2}\right)-\dfrac43\Cdota\dfrac12\Cdota\dfrac{\sqrt2}{2}
-\left(-4-\dfrac43\right) \\[4pt]
=&\dfrac{16}{3}-\dfrac{7\sqrt2}{3}
\end{align*}
であるから,
V&=2\left(\dfrac83-\dfrac{5\sqrt2}{3}+\dfrac{16}{3}-\dfrac{7\sqrt2}{3}\right) \\[4pt]
&=16-8\sqrt2
\end{align*}

上で出てきた $\dint{}{}\theta\cos\theta\;d\theta$ を求めるときに瞬間部分積分を利用している。

瞬間部分積分を知らない人は,次の記事から知識を吸収して,サクサク積分できるようにしよう。
立体の図を描くことについて

今回扱った2つの円柱が交わっている様子や2つの円柱の共通部分は次の図のようになる。
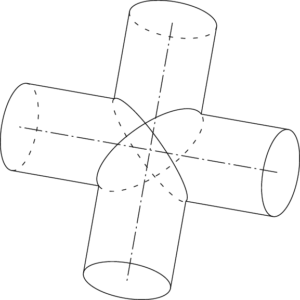
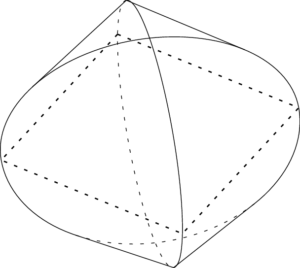

すぐに描けるなら描いた方が良いが,すらすらと描ける人の方が少ないだろう。しかも立体の図を描けなくても解ける。
- 描きにくければ無理に斜めから見た図を描かない。
- 座標軸の方向,平面に水平な方向,平面に垂直な方向から見た図を描く。
- 立体を無理にイメージしない。

問題によっては立体がどんな形か想像すらできないものもある。

それでも体積を求めないといけないのだから,立体の様子が分かる図を描く・描かないは関係ないということ。

どのようにして体積を求めるのかを考えることに時間を使うようにしよう。