ここでは3つの集合に関する様々な集合について説明します。
2つの集合の共通部分や和集合は簡単であっても,補集合も加わると少しややこしくなります。
集合が3つになると,さらに複雑になって考えにくくなります。
そのような少し複雑な集合についても,しっかりと考えることができるようにしておきましょう。
Contents
3つの集合の共通部分・和集合・補集合

ヒロ
集合が3つになっても考え方は2つのときと同じなので,落ち着いて考えれば解けるだろう。
問題次の集合が表す部分を次の図に斜線で表せ。
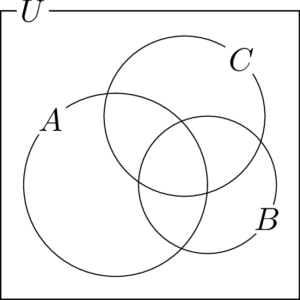
(1) $A\cap B\cap C$
(2) $A\cup B\cup C$
(3) $\overline{A}\cap\overline{B}\cap\overline{C}$
(4) $\overline{A}\cup\overline{B}\cup\overline{C}$

(1) $A\cap B\cap C$
(2) $A\cup B\cup C$
(3) $\overline{A}\cap\overline{B}\cap\overline{C}$
(4) $\overline{A}\cup\overline{B}\cup\overline{C}$

ヒロ
丁寧に考えることで,どの部分を表しているかはわかるだろう。
【解答】
(1) $A\cap B\cap C$
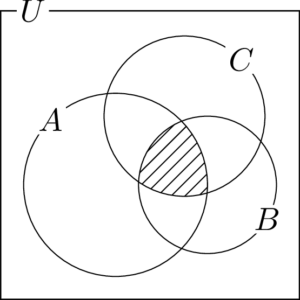
(2) $A\cup B\cup C$
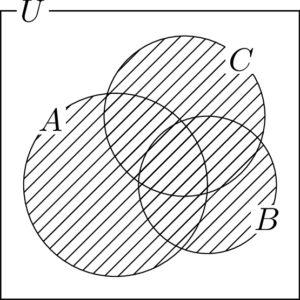
(3) $\overline{A}\cap\overline{B}\cap\overline{C}$
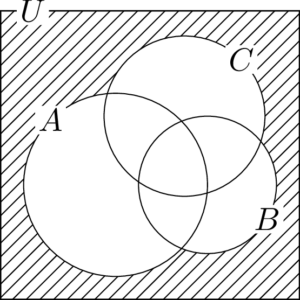
(4) $\overline{A}\cup\overline{B}\cup\overline{C}$

(1) $A\cap B\cap C$

(2) $A\cup B\cup C$

(3) $\overline{A}\cap\overline{B}\cap\overline{C}$

(4) $\overline{A}\cup\overline{B}\cup\overline{C}$

3つの集合のド・モルガンの法則

ヒロ
上の問題の結果から,ド・モルガンの法則を拡張することができる。
3つの集合のド・モルガンの法則3つの集合 $A,~B,~C$ について,次の式が成り立つ。
\begin{align*}
&\overline{A\cap B\cap C}=\overline{A}\cup\overline{B}\cup\overline{C} \\[4pt]
&\overline{A\cup B\cup C}=\overline{A}\cap\overline{B}\cap\overline{C}
\end{align*}
&\overline{A\cap B\cap C}=\overline{A}\cup\overline{B}\cup\overline{C} \\[4pt]
&\overline{A\cup B\cup C}=\overline{A}\cap\overline{B}\cap\overline{C}
\end{align*}
3つの集合の結合法則

ヒロ
次の問題で結合法則について確認してみよう。
問題次の集合が表す部分を次の図に斜線で表せ。

(1) $(A\cap B)\cap C$
(2) $A\cap(B\cap C)$
(3) $(A\cup B)\cup C$
(4) $A\cup(B\cup C)$

(1) $(A\cap B)\cap C$
(2) $A\cap(B\cap C)$
(3) $(A\cup B)\cup C$
(4) $A\cup(B\cup C)$
【解答】
(1) $(A\cap B)\cap C$
$A\cap B$ は $A$ と $B$ の共通部分であるから,次の図の斜線部分を表す。
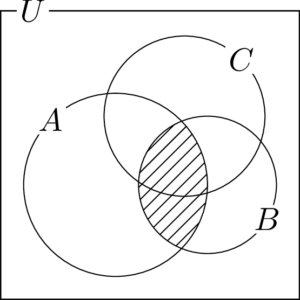
これと $C$ の共通部分が求めるものであるから,次の図の斜線部分になる。

(2) $A\cap(B\cap C)$
$B\cap C$ は $B$ と $C$ の共通部分であるから,次の図の斜線部分を表す。
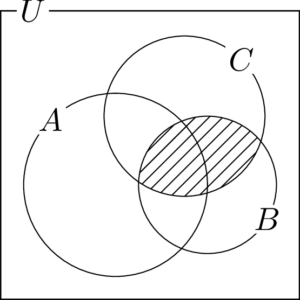
これと $A$ の共通部分が求めるものであるから,次の図の斜線部分になる。

(3) $(A\cup B)\cup C$
$A\cup B$ は $A$ と $B$ の和集合であるから,次の図の斜線部分を表す。

これと $C$ との和集合が求めるものであるから,次の図の斜線部分になる。

(4) $A\cup(B\cup C)$
$B\cup C$ は $B$ と $C$ の和集合であるから,次の図の斜線部分を表す。
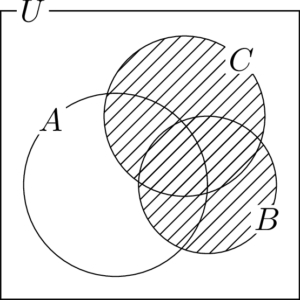
これと $A$ との和集合が求めるものであるから,次の図の斜線部分になる。

(1) $(A\cap B)\cap C$
$A\cap B$ は $A$ と $B$ の共通部分であるから,次の図の斜線部分を表す。

これと $C$ の共通部分が求めるものであるから,次の図の斜線部分になる。

(2) $A\cap(B\cap C)$
$B\cap C$ は $B$ と $C$ の共通部分であるから,次の図の斜線部分を表す。

これと $A$ の共通部分が求めるものであるから,次の図の斜線部分になる。

(3) $(A\cup B)\cup C$
$A\cup B$ は $A$ と $B$ の和集合であるから,次の図の斜線部分を表す。

これと $C$ との和集合が求めるものであるから,次の図の斜線部分になる。

(4) $A\cup(B\cup C)$
$B\cup C$ は $B$ と $C$ の和集合であるから,次の図の斜線部分を表す。

これと $A$ との和集合が求めるものであるから,次の図の斜線部分になる。


ヒロ
この問題の結果から,共通部分$(\cap)$や和集合$(\cup)$のみで表されたものは演算順序は問われないことが分かる。
結合法則3つの集合 $A,~B,~C$ に対して,次の式が成り立つ。
\begin{align*}
&(A\cap B)\cap C=A\cap(B\cap C) \\[4pt]&(A\cup B)\cup C=A\cup(B\cup C)
\end{align*}
&(A\cap B)\cap C=A\cap(B\cap C) \\[4pt]&(A\cup B)\cup C=A\cup(B\cup C)
\end{align*}
3つの集合の分配法則

ヒロ
次の問題で分配法則について確認してみよう。
問題次の集合が表す部分を次の図に斜線で表せ。

(1) $(A\cap B)\cup C$
(2) $(A\cup C)\cap(B\cup C)$
(3) $(A\cup B)\cap C$
(4) $(A\cap C)\cup(B\cap C)$

(1) $(A\cap B)\cup C$
(2) $(A\cup C)\cap(B\cup C)$
(3) $(A\cup B)\cap C$
(4) $(A\cap C)\cup(B\cap C)$
【解答】
(1) $(A\cap B)\cup C$
$A\cap B$ は次の図の斜線部分である。

求める部分は,上の斜線部分と $C$ との和集合であるから,次の図の斜線部分である。
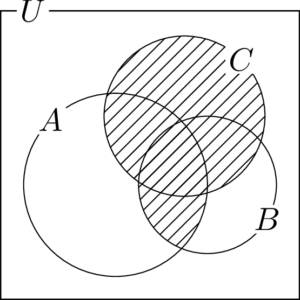
(2) $(A\cup C)\cap(B\cup C)$
$A\cup C$ は次の図の斜線部分である。
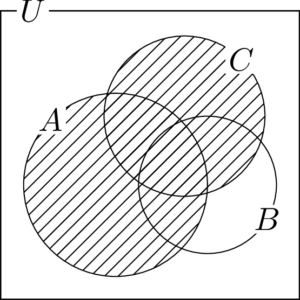
$B\cup C$ は次の図の斜線部分である。

求める部分は,2つの図の共通部分であるから,次の図の斜線部分である。

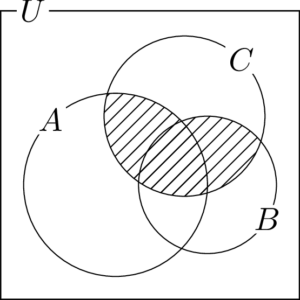
(3) $(A\cup B)\cap C$
$A\cup B$ は次の図の斜線部分である。

求める部分は,上の斜線部分と $C$ との共通部分であるから,次の図の斜線部分である。
(4) $(A\cap C)\cup(B\cap C)$
$A\cap C$ は次の図の斜線部分である。
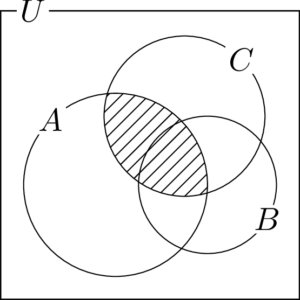
$B\cap C$ は次の図の斜線部分である。

求める部分は,2つの図の和集合であるから,次の図の斜線部分である。

(1) $(A\cap B)\cup C$
$A\cap B$ は次の図の斜線部分である。

求める部分は,上の斜線部分と $C$ との和集合であるから,次の図の斜線部分である。

(2) $(A\cup C)\cap(B\cup C)$
$A\cup C$ は次の図の斜線部分である。

$B\cup C$ は次の図の斜線部分である。

求める部分は,2つの図の共通部分であるから,次の図の斜線部分である。

(3) $(A\cup B)\cap C$
$A\cup B$ は次の図の斜線部分である。

求める部分は,上の斜線部分と $C$ との共通部分であるから,次の図の斜線部分である。

(4) $(A\cap C)\cup(B\cap C)$
$A\cap C$ は次の図の斜線部分である。

$B\cap C$ は次の図の斜線部分である。

求める部分は,2つの図の和集合であるから,次の図の斜線部分である。


ヒロ
この問題の結果から,次の分配法則が成り立つことが分かる。
分配法則3つの集合 $A,~B,~C$ に対して,次の式が成り立つ。
\begin{align*}
&(A\cap B)\cup C=(A\cup C)\cap(B\cup C) \\[4pt]&(A\cup B)\cap C=(A\cap C)\cup(B\cap C)
\end{align*}
&(A\cap B)\cup C=(A\cup C)\cap(B\cup C) \\[4pt]&(A\cup B)\cap C=(A\cap C)\cup(B\cap C)
\end{align*}
定期テストで出題された問題

ヒロ
それでは実際に定期テストで出題された問題を解いてみよう。
問題次の式の表す集合を次の図に斜線をつけて示せ。ただし全体集合を $U$ とする。

(1) $\overline{A}\cap(B\cup C)$
(2) $\overline{A\cap B}\cup C$

(1) $\overline{A}\cap(B\cup C)$
(2) $\overline{A\cap B}\cup C$
【考え方と解答】
(1) $\overline{A}(B\cup C)$
$B\cup C$ は次の斜線部分を表す。

求める部分は,これと $A$ の補集合との共通部分であるから,次の図の斜線部分となる。
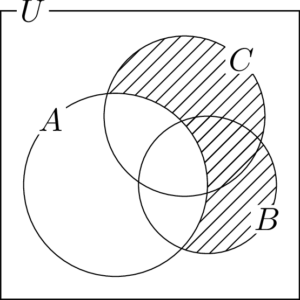
(2) $\overline{A\cap B}\cup C$
$\overline{A\cap B}$ は次の斜線部分を表す。

求める部分は,これと $C$ との和集合がであるから,次の図の斜線部分となる。

(1) $\overline{A}(B\cup C)$
$B\cup C$ は次の斜線部分を表す。

求める部分は,これと $A$ の補集合との共通部分であるから,次の図の斜線部分となる。

(2) $\overline{A\cap B}\cup C$
$\overline{A\cap B}$ は次の斜線部分を表す。

求める部分は,これと $C$ との和集合がであるから,次の図の斜線部分となる。

定期テストで出題された問題2
問題1から10までの整数を全体集合,
(1) $(A\cap B)\cup C$
(2) $A\cap(B\cup C)$
(3) $\overline{A}\cap(B\cup C)$
\begin{align*}
&A=\{1,~3,~5,~7,~9\} \\[4pt]&B=\{2,~3,~4,~5,~6\} \\[4pt]&C=\{3,~6,~8,~9\}
\end{align*}
とするとき,次の集合を求めよ。&A=\{1,~3,~5,~7,~9\} \\[4pt]&B=\{2,~3,~4,~5,~6\} \\[4pt]&C=\{3,~6,~8,~9\}
\end{align*}
(1) $(A\cap B)\cup C$
(2) $A\cap(B\cup C)$
(3) $\overline{A}\cap(B\cup C)$
【考え方と解答】
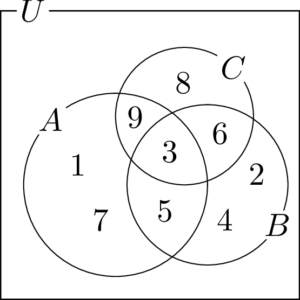
3つの集合の要素を見ると,3つの集合 $A,~B,~C$ のどの2つに対しても共通部分が存在するから,次のベン図を利用して要素を書き込んでいく。

条件が厳しい部分から考えていくのが良い。つまり,より多くの集合が重なっている部分から考えていくのが良い。
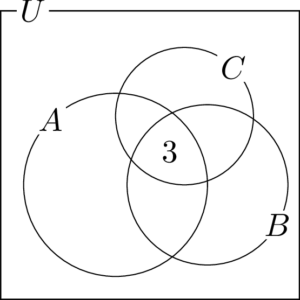
$A\cap B\cap C=\{3\}$ より3つの集合の共通部分に3を書く。
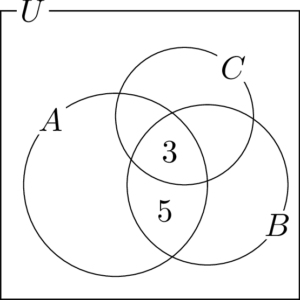
次に $A\cap B=\{3,~5\}$ であるから,$A$ と $B$ の共通部分で $C$ の外部に5を書く。
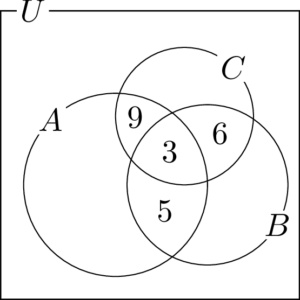
$B\cap C=\{3,~6\}$,$A\cap C=\{3,~9\}$ であるから,先程と同様にそれぞれ6と9を書く。
それぞれの集合で書いていない要素を書いていく。$A$ の要素で $B$ にも $C$ にも含まれない要素は1と7であり,これらを$A$ の内部だけど $B$ と $C$ の外部になる部分($A\cap\overline{B\cup C}$)に書く。
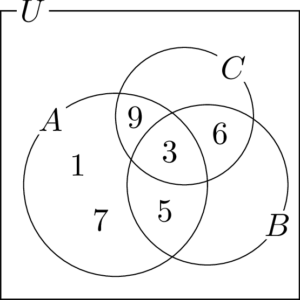
同じように $A,~B,~C$ のうち,$B$ だけに含まれる要素や $C$ だけに含まれる要素を書く。
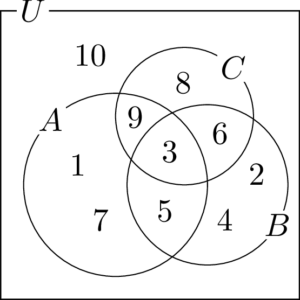
全体集合が10以下の自然数だから,書いていない整数を調べると10が残っていることが分かる。10を $A,~B,~C$ の和集合の外側に書く。
(1) $(A\cap B)\cup C$
$(A\cap B)\cup C$ が表す部分は次の図の斜線部分である。

よって,
(2) $A\cap(B\cup C)$
$A\cap(B\cup C)$ が表す部分は次の図の斜線部分である。
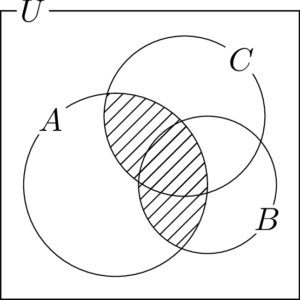
よって,
(3) $\overline{A}\cap(B\cup C)$
$\overline{A}\cap(B\cup C)$ が表す部分は次の図の斜線部分である。

よって,
3つの集合の要素を見ると,3つの集合 $A,~B,~C$ のどの2つに対しても共通部分が存在するから,次のベン図を利用して要素を書き込んでいく。

条件が厳しい部分から考えていくのが良い。つまり,より多くの集合が重なっている部分から考えていくのが良い。
$A\cap B\cap C=\{3\}$ より3つの集合の共通部分に3を書く。

次に $A\cap B=\{3,~5\}$ であるから,$A$ と $B$ の共通部分で $C$ の外部に5を書く。

$B\cap C=\{3,~6\}$,$A\cap C=\{3,~9\}$ であるから,先程と同様にそれぞれ6と9を書く。

それぞれの集合で書いていない要素を書いていく。$A$ の要素で $B$ にも $C$ にも含まれない要素は1と7であり,これらを$A$ の内部だけど $B$ と $C$ の外部になる部分($A\cap\overline{B\cup C}$)に書く。

同じように $A,~B,~C$ のうち,$B$ だけに含まれる要素や $C$ だけに含まれる要素を書く。

全体集合が10以下の自然数だから,書いていない整数を調べると10が残っていることが分かる。10を $A,~B,~C$ の和集合の外側に書く。

(1) $(A\cap B)\cup C$
$(A\cap B)\cup C$ が表す部分は次の図の斜線部分である。

よって,
\begin{align*}
(A\cap B)\cup C=\{3,~5,~6,~8,~9\}
\end{align*}
(A\cap B)\cup C=\{3,~5,~6,~8,~9\}
\end{align*}
(2) $A\cap(B\cup C)$
$A\cap(B\cup C)$ が表す部分は次の図の斜線部分である。

よって,
\begin{align*}
A\cap(B\cup C)=\{3,~5,~9\}
\end{align*}
A\cap(B\cup C)=\{3,~5,~9\}
\end{align*}
(3) $\overline{A}\cap(B\cup C)$
$\overline{A}\cap(B\cup C)$ が表す部分は次の図の斜線部分である。

よって,
\begin{align*}
\overline{A}\cap(B\cup C)=\{2,~4,~6,~8\}
\end{align*}
\overline{A}\cap(B\cup C)=\{2,~4,~6,~8\}
\end{align*}

ヒロ
3つの集合の共通部分や和集合については複雑なものがあるが,丁寧に1つずつ考えるようにすることが大切である。




















