外積を利用した2つのベクトルに垂直なベクトルの求め方とは？

Contents

1つのベクトルの成分に0がない場合

さっきは成分に0が含まれていたから簡単にできましたけど，そうじゃない場合はどうするんですか？

ヒロ

次の問題で解説していくよ。

2018年慶應義塾大・薬学部座標空間に4点 $\mathrm{O}(0,0,0)$，$\mathrm{A}(3,-2,-1)$，$\mathrm{B}(1,1,1)$，$\mathrm{C}(-1,4,2)$ がある。
$\Vec{OA}$，$\Vec{BC}$のどちらにも垂直で長さが $3\sqrt{3}$ であるベクトルを成分で表すと，$\myhako$ である。

プリントを次のリンクからダウンロードできます。

ダウンロード

ヒロ

まず，$\Vec{OA},\Vec{BC}$ の成分を求めよう。

それは任せて下さい！

\begin{align*}
\Vec{OA}=(3,-2,-1),~\Vec{BC}=(-2,3,1)
\end{align*}

ヒロ

外積を利用して2つのベクトルに垂直なベクトルを求める方法をマスターしよう。通常，高校では習わないけど，知っておくと得・・・というか知らないと損なので教えておくよ。

ヒロ

まず，$\vec{a}=(a_1,~a_2,~a_3),~\vec{b}=(b_1,~b_2,~b_3)$とすると，
$\vec{a}$と$\vec{b}$ の外積は次のようになる。

\begin{align*}
\vec{a}\times\vec{b}=(a_2b_3-a_3b_2,~a_3b_1-a_1b_3,~a_1b_2-a_2b_1)
\end{align*}

これを覚えるんですか・・・？

ヒロ

そのまま覚えてって言っても，覚えにくいと思うので，次のように覚えよう。

ヒロ

まず，$\vec{a}$ の成分を $x$ 成分，$y$ 成分，$z$ 成分，$x$ 成分の順に並べて，その下に $\vec{b}$ の成分を $\vec{a}$ と同じ順に並べよう。あとはクロスに掛けて引く。成分は①，②，③の順に $x,y,z$ となるよ。

ヒロ

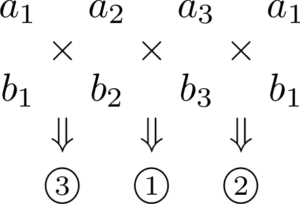
①，②，③は次の計算規則に従って計算しよう。

ヒロ

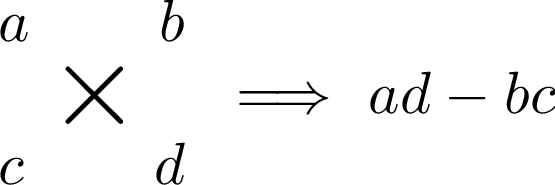
とりあえず，このルールで $\Vec{OA}\times\Vec{BC}$ を求めてみよう。

やってみます！

\begin{align*}
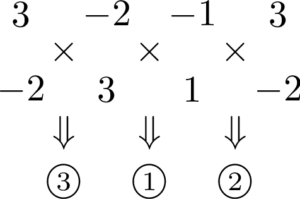
①&=-2\times1-(-1)\times3 \\[4pt]&=-2+3 \\[4pt]&=1 \\[4pt]②&=-1\times(-2)-3\times1 \\[4pt]&=2-3 \\[4pt]&=-1 \\[4pt]③&=3\times3-(-2)\times(-2) \\[4pt]&=9-4 \\[4pt]&=5
\end{align*}

よって，$\Vec{OA}\times\Vec{BC}=(1,-1,5)$

出来ました！

ヒロ

じゃあ， $\Vec{OA}\times\Vec{BC}$ と $\Vec{OA},~\Vec{BC}$ の内積を計算してみて？

はい！

\begin{align*}
(\Vec{OA}\times\Vec{BC})\Cdota\Vec{OA}&=(1,-1,5)\Cdota(3,-2,-1) \\[4pt]&=3+2-5 \\[4pt]&=0 \\[4pt](\Vec{OA}\times\Vec{BC})\Cdota\Vec{BC}&=(1,-1,5)\Cdota(-2,3,1) \\[4pt]&=-2-3+5 \\[4pt]&=0
\end{align*}