異なるものを円形に並べる問題なら比較的簡単ですが,同じものを含むものを円形に並べる問題になるとややこしくなります。
比較的レベルの高い高校であれば,そのような難しい問題も定期テストに出題されて鍛えられます。
しかし,標準レベルの高校だとそのような難しい問題は定期テストに出題されず,模擬テストを受けたときに初めて見て白紙解答になってしまって落ち込むことになります。
そんなことにならないように,しっかりと考え方を身に付けて基礎力をアップさせましょう。
同じものを含む円順列の総数を求める問題

ヒロ
実際に高校の定期テストで出題された問題を解説していく。
問題青玉2個,白玉5個,黒玉1個がある。
(1) これらを円形に並べる方法は何通りあるか。
(2) (1)の円の中心を通る直線に関して対称な円順列は何通りあるか。
(3) これらの玉にひもを通して輪を作る方法は何通りあるか。
(1) これらを円形に並べる方法は何通りあるか。
(2) (1)の円の中心を通る直線に関して対称な円順列は何通りあるか。
(3) これらの玉にひもを通して輪を作る方法は何通りあるか。

ヒロ
円順列の基本は「1つを固定すること」だね。

ヒロ
これは同じものを含むものを円形に並べるときも基本的には変わらない。
【(1)の考え方と解答】
1個の黒玉を固定して考えると,求める場合の数は青玉2個,白玉5個を1列に並べる方法の総数に等しいから
1個の黒玉を固定して考えると,求める場合の数は青玉2個,白玉5個を1列に並べる方法の総数に等しいから
\begin{align*}
\dfrac{7!}{2!5!}=\dfrac{7\Cdot6}{2\Cdot1}=21~通り
\end{align*}
\dfrac{7!}{2!5!}=\dfrac{7\Cdot6}{2\Cdot1}=21~通り
\end{align*}
(2) (1)の円の中心を通る直線に関して対称な円順列は何通りあるか。
【(2)の考え方と解答】
具体的に1つの並び方を考えてみよう。
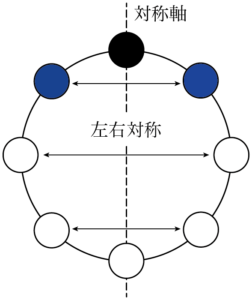
上の図のように並べると,線対称になる並べ方のときは黒玉と白玉が対称軸上にあることが分かる。1つの並べ方ですぐに分からない場合は,具体的にどんどん作ることで分かるはず。
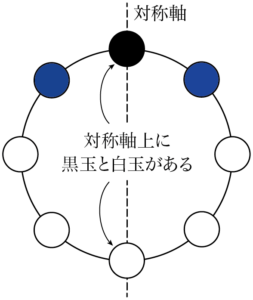
これによって,対称軸の右側と左側にはそれぞれ青玉1個,白玉2個があることも分かる。
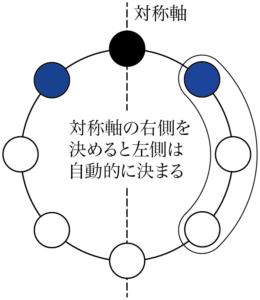
また,対称軸の右側と左側の片側を決めると,線対称に並べることから,もう一方の並べ方は自動的に決まる。
決めるのは右側と左側のどちらでも良いが,右側に青玉1個と白玉2個を並べた時点で対称な円順列が1つ決まることになる。
よって,求める場合の数は
具体的に1つの並び方を考えてみよう。

上の図のように並べると,線対称になる並べ方のときは黒玉と白玉が対称軸上にあることが分かる。1つの並べ方ですぐに分からない場合は,具体的にどんどん作ることで分かるはず。

これによって,対称軸の右側と左側にはそれぞれ青玉1個,白玉2個があることも分かる。
また,対称軸の右側と左側の片側を決めると,線対称に並べることから,もう一方の並べ方は自動的に決まる。
決めるのは右側と左側のどちらでも良いが,右側に青玉1個と白玉2個を並べた時点で対称な円順列が1つ決まることになる。

よって,求める場合の数は
\begin{align*}
\dfrac{3!}{2!}=3~通り
\end{align*}
\dfrac{3!}{2!}=3~通り
\end{align*}
(3) これらの玉にひもを通して輪を作る方法は何通りあるか。
【(3)の考え方と解答】
ひもを通して輪にする場合は,裏返して同じ並べ方になるものに注意する必要がある。
したがって「線対称な並べ方」と「線対称ではない並べ方」に着目する。
いま,(1)と(2)の結果から,線対称な並べ方が3通りあり,線対称ではない並べ方は $21-3=18$ 通りあることが分かる。
線対称ではない並べ方を1つ取り出して裏返すと,18通りある線対称ではない別の並べ方になるが,輪として見ると,この2つの並べ方は同じ並べ方であると考えなければならない。
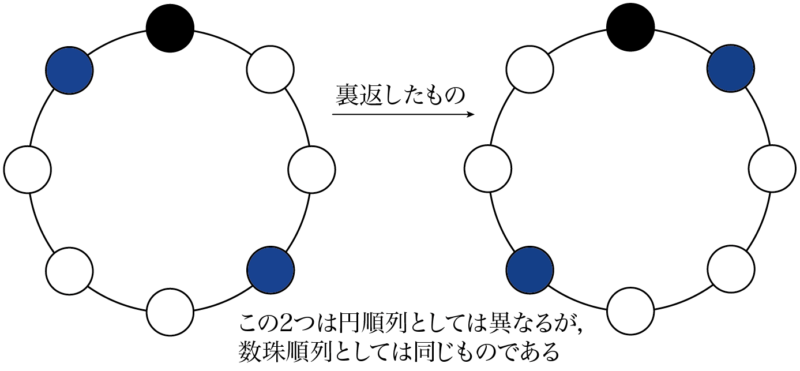
つまり線対称ではない並べ方は18通りあるが,2通りずつ,互いに裏返した並べ方になっているため,ひもを通して輪にするとその半分の9通りしかないことになる。
一方で,3通りある線対称な並べ方を裏返しても,別の線対称な並べ方にはならないため,ひもを通して輪にしても3通りの輪を作ることができる。
したがって,求める場合の数は
ひもを通して輪にする場合は,裏返して同じ並べ方になるものに注意する必要がある。
したがって「線対称な並べ方」と「線対称ではない並べ方」に着目する。
いま,(1)と(2)の結果から,線対称な並べ方が3通りあり,線対称ではない並べ方は $21-3=18$ 通りあることが分かる。
線対称ではない並べ方を1つ取り出して裏返すと,18通りある線対称ではない別の並べ方になるが,輪として見ると,この2つの並べ方は同じ並べ方であると考えなければならない。

つまり線対称ではない並べ方は18通りあるが,2通りずつ,互いに裏返した並べ方になっているため,ひもを通して輪にするとその半分の9通りしかないことになる。
一方で,3通りある線対称な並べ方を裏返しても,別の線対称な並べ方にはならないため,ひもを通して輪にしても3通りの輪を作ることができる。
したがって,求める場合の数は
\begin{align*}
3+\dfrac{21-3}{2}=12~通り
\end{align*}
3+\dfrac{21-3}{2}=12~通り
\end{align*}

ヒロ
公式として処理したい人は次のポイントを覚えておこう。
同じものを含む数珠順列同じものを含む数珠順列の総数は
\begin{align*}
(左右非対称の個数)+\dfrac{(左右対称の個数)}{2}
\end{align*}
で求めることができる。(左右非対称の個数)+\dfrac{(左右対称の個数)}{2}
\end{align*}
同じものを含む円順列の総数を求める問題2

ヒロ
次の問題を考えてみよう。
問題白球6個,赤球3個,合計9個の球がある。
(1) これら9個の球を円形に並べる方法は全部で何通りあるか。
(2) これら9個の球をすべて使ってできる数珠は全部で何通りあるか。
(1) これら9個の球を円形に並べる方法は全部で何通りあるか。
(2) これら9個の球をすべて使ってできる数珠は全部で何通りあるか。

ヒロ
色が2種類になって解きやすいかと思うと,実はそうではない。

ヒロ
次のような誤答をよく目にする。
【(1)のよくある誤答】
円順列では1つの球を固定するのが基本だから,赤球を固定する。このとき,白球6個と赤球2個を1列に並べる方法を考えて
円順列では1つの球を固定するのが基本だから,赤球を固定する。このとき,白球6個と赤球2個を1列に並べる方法を考えて
\begin{align*}
\dfrac{8!}{6!2!}=\dfrac{8\Cdot7}{2\Cdot1}=28~通り
\end{align*}
\dfrac{8!}{6!2!}=\dfrac{8\Cdot7}{2\Cdot1}=28~通り
\end{align*}

ヒロ
これは実は同じ並べ方を重複して数えている。
【1つを固定しても同じ並べ方が現れる】
赤球をRとし,白球をWと表すことにする。赤球1つを固定したとき,残りの部分に2個のRと6個のWを並べることになる。
例えば「WRWWWRWW」と並べると,次のようになる。
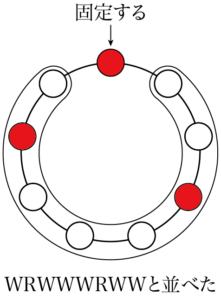
また別の並べ方として「WWRWRWWW」と並べると,次のようになる。
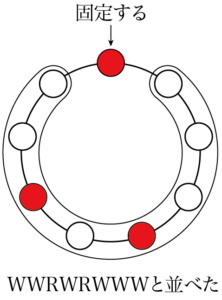
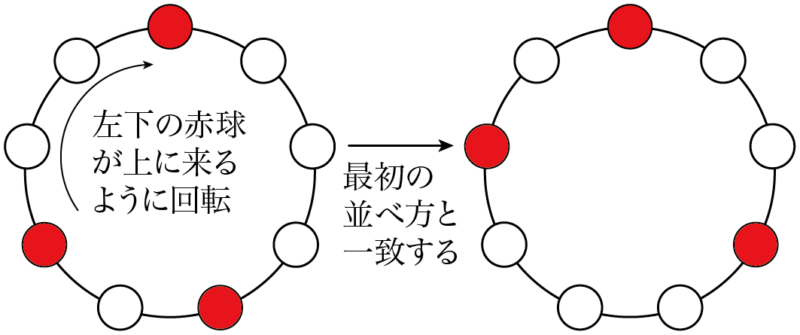
1列に並べる方法としては別の並べ方であるが,よく見ると,3つ分時計回りに回転させると,2つの並べ方は一致して同じ並べ方であることが分かる。
赤球をRとし,白球をWと表すことにする。赤球1つを固定したとき,残りの部分に2個のRと6個のWを並べることになる。
例えば「WRWWWRWW」と並べると,次のようになる。

また別の並べ方として「WWRWRWWW」と並べると,次のようになる。

1列に並べる方法としては別の並べ方であるが,よく見ると,3つ分時計回りに回転させると,2つの並べ方は一致して同じ並べ方であることが分かる。


ヒロ
今まではうまくいっていた「1つのものを固定する」という手法が使えないことが分かる。

ヒロ
最初の問題では仲間外れのような黒玉が1個あるおかげで,こういった事態を避けることができていたことも分かるね。

ヒロ
今回の問題では,3個ある赤球の配置によって場合分けして考える必要がある。
【(1)の考え方と解答】
赤球の配置に着目すると,次の3つのタイプに分類することができる。
(i) 3個すべてが隣り合う
(ii) 2個と1個に分かれる
(iii) 1個ずつバラバラ
1つずつ順番に考えていこう。
(i)のときは明らかに1通りしかないことが分かる。
(ii)のときは2個と1個の間に白球が何個入るかを考える必要がある。
次の図のように $x$ 個と $y$ 個とする。
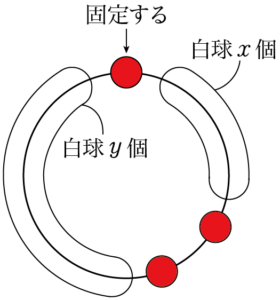
$x,~y$ は
(iii)のとき,(ii)のときと同じように赤球の間に入る白球の個数に着目する。
次の図のように白球の個数を $x,~y,~z$ とする。
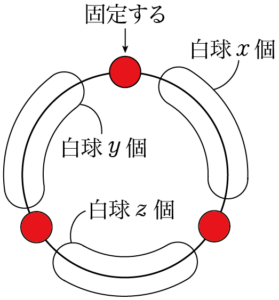
$x,~y,~z$ は
$(2,~2,~2)$ は数字の入れ替えがそもそもないため,円順列としても1通りである。
$(1,~1,~4)$ に対して入れ替えを考えると,他に $(1,~4,~1)$, $(4,~1,~1)$ が考えられるから,次の3つの図のようになる。
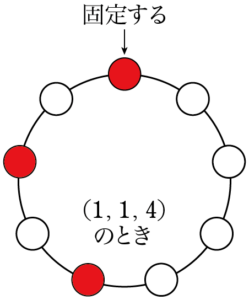
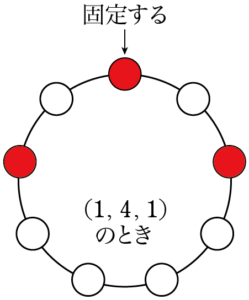
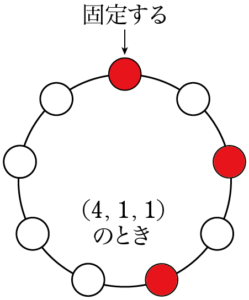
3つの並べ方は異なるように見えるが,回転させるとすべて一致するから円順列としては1通りであることが分かる。
$(1,~2,~3)$ については,並べ方は $3!=6$ 通りある。この6通りの中で同じものがあるかどうかを調べる必要がある。「たった6通りなら全部書いて調べれば良い」と考えたときは次の6つの図を見て,円順列としては何通りあるかを数えよう。
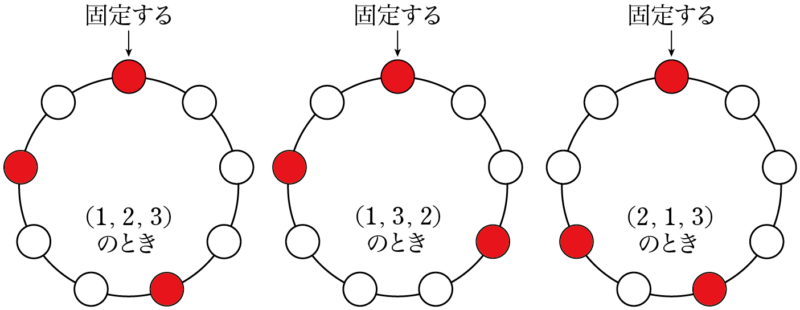
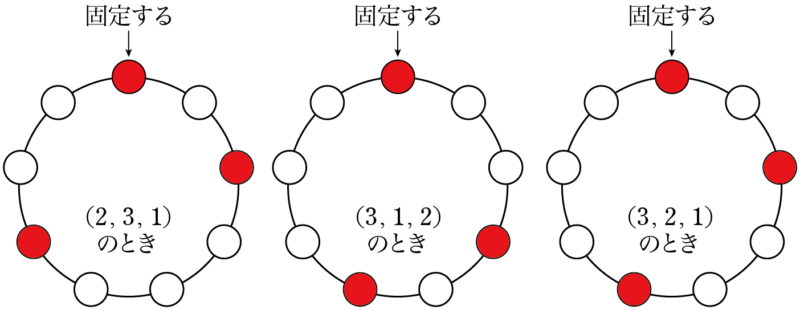
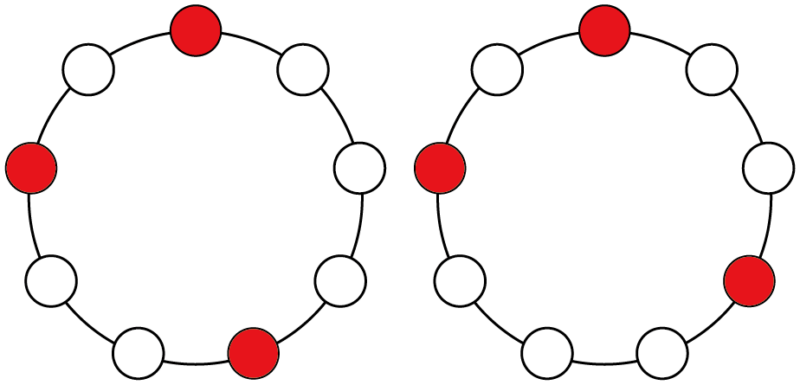
よく見ると次の2通りになることが分かる。
「6通りも書いてられるか!」という人は「白赤白」のカタマリを固定して考えると良い。
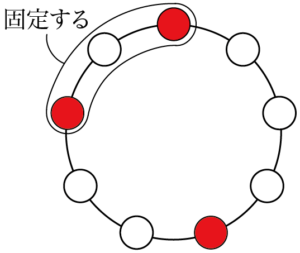
上の図のように「白赤白」を固定すると白球2個のカタマリ・赤球1個・白球3個のカタマリを1列に並べるが,白球2個のカタマリと白球3個のカタマリが隣り合ってはいけないことを考えると2通りしかないことが分かる。
よって,(iii)のときは $1+1+2=4$ 通り。
したがって,(i)~(iii)より
赤球の配置に着目すると,次の3つのタイプに分類することができる。
(i) 3個すべてが隣り合う
(ii) 2個と1個に分かれる
(iii) 1個ずつバラバラ
1つずつ順番に考えていこう。
(i)のときは明らかに1通りしかないことが分かる。
(ii)のときは2個と1個の間に白球が何個入るかを考える必要がある。
次の図のように $x$ 個と $y$ 個とする。

$x,~y$ は
\begin{align*}
x+y=6,~x\geqq1,~y\geqq1
\end{align*}
を満たす整数であるからx+y=6,~x\geqq1,~y\geqq1
\end{align*}
\begin{align*}
(x,~y)=(1,~5),~(2,~4),~(3,~3),~(4,~2),~(5,~1)
\end{align*}
となる。よって,5通り。(x,~y)=(1,~5),~(2,~4),~(3,~3),~(4,~2),~(5,~1)
\end{align*}
(iii)のとき,(ii)のときと同じように赤球の間に入る白球の個数に着目する。
次の図のように白球の個数を $x,~y,~z$ とする。

$x,~y,~z$ は
\begin{align*}
x+y+z=6,~x\geqq1,~y\geqq1,~z\geqq1
\end{align*}
を満たす整数である。大小関係を定めずに書き出すと大変なので,とりあえず大小関係を $x\leqq y\leqq z$ と定めて考える。このとき $x,~y,z$ の組合せはx+y+z=6,~x\geqq1,~y\geqq1,~z\geqq1
\end{align*}
\begin{align*}
(x,~y,~z)&=(1,~1,~4),~(1,~2,~3),~(2,~2,~2)
\end{align*}
の3通りになる。考えやすいものから1つずつ確認していく。(x,~y,~z)&=(1,~1,~4),~(1,~2,~3),~(2,~2,~2)
\end{align*}
$(2,~2,~2)$ は数字の入れ替えがそもそもないため,円順列としても1通りである。
$(1,~1,~4)$ に対して入れ替えを考えると,他に $(1,~4,~1)$, $(4,~1,~1)$ が考えられるから,次の3つの図のようになる。



3つの並べ方は異なるように見えるが,回転させるとすべて一致するから円順列としては1通りであることが分かる。
$(1,~2,~3)$ については,並べ方は $3!=6$ 通りある。この6通りの中で同じものがあるかどうかを調べる必要がある。「たった6通りなら全部書いて調べれば良い」と考えたときは次の6つの図を見て,円順列としては何通りあるかを数えよう。


よく見ると次の2通りになることが分かる。

「6通りも書いてられるか!」という人は「白赤白」のカタマリを固定して考えると良い。

上の図のように「白赤白」を固定すると白球2個のカタマリ・赤球1個・白球3個のカタマリを1列に並べるが,白球2個のカタマリと白球3個のカタマリが隣り合ってはいけないことを考えると2通りしかないことが分かる。
よって,(iii)のときは $1+1+2=4$ 通り。
したがって,(i)~(iii)より
\begin{align*}
1+5+4=10~通り
\end{align*}
1+5+4=10~通り
\end{align*}
(2) これら9個の球をすべて使ってできる数珠は全部で何通りあるか。

ヒロ
次は数珠を作るから裏返したときに同じものになる並べ方に注意しよう。
【(2)の考え方と解答】
(1)の円順列の10通りのうち,裏返したときに,同じ数珠になるものに注意しよう。
(1)と同様に,次の3つのタイプに分類して考える。
(i) 3個すべてが隣り合う
(ii) 2個と1個に分かれる
(iii) 1個ずつバラバラ
(i)は円順列でも1通りしかないため,数珠順列でも1通り。
(ii)は $x,~y$ の5つの組合せのうち,$(1,~5)$ と $(5,~1)$ は次の図を見れば同じ数珠になることが分かる。
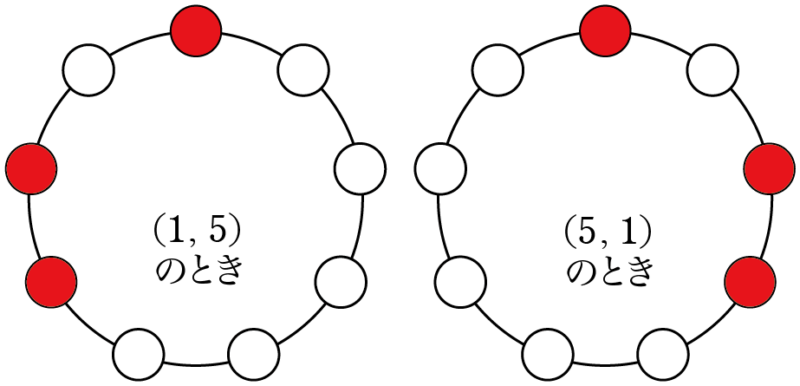
また,$(1,~4)$ と $(4,~1)$ も同じ数珠になるから,$(3,~3)$ の場合を合わせて作れる数珠は3通りある。
(iii)は $(2,~2,~2)$ と $(1,~1,~4)$ は円順列でもそれぞれ1通りしかないから,数珠順列でも1通りずつになる。
$(1,~2,~3)$ の組合せは円順列では2通りあったが,数珠になると互いに裏返したものであるから1通りしかない。
よって,(iii)のときは $1+1+1=3$ 通り。
したがって,求める場合の数は
(1)の円順列の10通りのうち,裏返したときに,同じ数珠になるものに注意しよう。
(1)と同様に,次の3つのタイプに分類して考える。
(i) 3個すべてが隣り合う
(ii) 2個と1個に分かれる
(iii) 1個ずつバラバラ
(i)は円順列でも1通りしかないため,数珠順列でも1通り。
(ii)は $x,~y$ の5つの組合せのうち,$(1,~5)$ と $(5,~1)$ は次の図を見れば同じ数珠になることが分かる。

また,$(1,~4)$ と $(4,~1)$ も同じ数珠になるから,$(3,~3)$ の場合を合わせて作れる数珠は3通りある。
(iii)は $(2,~2,~2)$ と $(1,~1,~4)$ は円順列でもそれぞれ1通りしかないから,数珠順列でも1通りずつになる。
$(1,~2,~3)$ の組合せは円順列では2通りあったが,数珠になると互いに裏返したものであるから1通りしかない。
よって,(iii)のときは $1+1+1=3$ 通り。
したがって,求める場合の数は
\begin{align*}
1+3+3=7~通り
\end{align*}
1+3+3=7~通り
\end{align*}


















