放物線上の2点を通る直線の式を求める機会はそれなりにありますが,意外と面倒ですよね。
これについて説明しているサイトは数多くありますが,そのどれもが頂点を原点とするタイプの放物線について解説しているだけです。中学生にとってはありがたい知識でも高校生にとっては既に知っていて,がっかりすることも少なくありません。
この記事を読むことで,どんな放物線でも,その放物線上の2点を通る直線の式を簡単に求めることができるようになります。
Contents
放物線 $y=ax^2$ 上の2点を通る直線の式を簡単に求める方法
プリントを次のリンクからダウンロードできます。

ヒロ
放物線 $y=ax^2$ 上の2点を通る直線の方程式は次のように表されることを知っておこう。
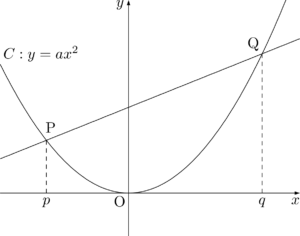
放物線 $y=ax^2$ 上の2点を通る直線の式放物線 $y=ax^2$ 上の2点 $\mathrm{P}(p,~ap^2)$, $\mathrm{Q}(q,~aq^2)$ を通る直線の方程式は次のようになる。
\begin{align*}
y=a(p+q)x-apq
\end{align*}
y=a(p+q)x-apq
\end{align*}


ヒロ
$x^2$ の係数と通る2点の $x$ 座標が分かっていれば,その2点を通る直線の式を簡単に求めることができる。そのため,高校入試であれば,かなり実用的な公式だね。

ヒロ
念のため,証明をしておこう。
【$y=ax^2$ 上の2点を通る直線の式の導出】
$y=ax^2$ 上の2点 $\mathrm{P}(p,~ap^2)$, $\mathrm{Q}(q,~aq^2)$ を通る直線の傾きを $m$ とすると
$y=ax^2$ 上の2点 $\mathrm{P}(p,~ap^2)$, $\mathrm{Q}(q,~aq^2)$ を通る直線の傾きを $m$ とすると
\begin{align*}
m&=\dfrac{ap^2-aq^2}{p-q} \\[4pt]&=\dfrac{a(p+q)(p-q)}{p-q} \\[4pt]&=a(p+q)
\end{align*}
よって,求める直線の方程式はm&=\dfrac{ap^2-aq^2}{p-q} \\[4pt]&=\dfrac{a(p+q)(p-q)}{p-q} \\[4pt]&=a(p+q)
\end{align*}
\begin{align*}
y&=a(p+q)(x-p)+ap^2 \\[4pt]&=a(p+q)x-apq
\end{align*}
y&=a(p+q)(x-p)+ap^2 \\[4pt]&=a(p+q)x-apq
\end{align*}
2004年 センター数学ⅡB 微積

ヒロ
それでは公式を使う練習として,2004年のセンター数学ⅡBの問題を解いてみよう。
2004年 センター試験 数学ⅡB 微積座標平面上の放物線 $y=x^2$ を $C$ とする。$a$ は $a\neq1$ を満たす実数とし,$C$ 上に点$\mathrm{P}(a+1,~(a+1)^2)$ と点 $\mathrm{Q}(2a,~4a^2)$ をとる。2点P, Qを通る直線を $\ell$ とすると,$\ell$ の方程式は
\begin{align*}
y=\left(\myBox{ア}~a+\myBox{イ}\right)x-\myBox{ウ}~a^2-\myBox{エ}~a
\end{align*}
y=\left(\myBox{ア}~a+\myBox{イ}\right)x-\myBox{ウ}~a^2-\myBox{エ}~a
\end{align*}

ヒロ
$x^2$ の係数と,2点P, Qの $x$ 座標に着目して求めよう。
【解答】
$x^2$ の係数が1で,2点P, Qの $x$ 座標がそれぞれ $a+1,~2a$ であるから,$\ell$ の方程式は
$x^2$ の係数が1で,2点P, Qの $x$ 座標がそれぞれ $a+1,~2a$ であるから,$\ell$ の方程式は
\begin{align*}
y&=(a+1+2a)x-2a(a+1) \\[4pt]
&=(3a+1)x-2a^2-2a
\end{align*}
y&=(a+1+2a)x-2a(a+1) \\[4pt]
&=(3a+1)x-2a^2-2a
\end{align*}

ヒロ
しかし,大学入試で出題される放物線は,このセンター試験のように原点が頂点になることはほとんどない。そのため,この公式の出番はほとんどなくなる。

ヒロ
そこで,考え方を変えることで,一般的な放物線でも使えるようにしよう。




















