Contents
- ページ1
- 1 1つのベクトルの成分に0がある場合
- ページ2
- 1 垂線の足の座標
- ページ3
- 1 1つのベクトルの成分に0がない場合
- ページ4
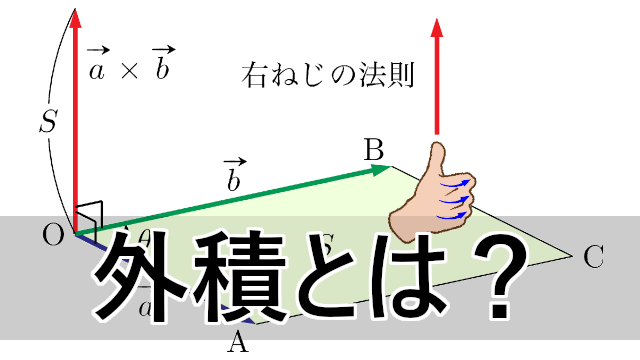
- 1 外積の性質
- ページ5
- 1 四面体の体積
- 2 まとめ
垂線の足の座標

ヒロ
ちなみに,問題では求めることは聞かれてないけど,点Hの座標もついでに求めておこう。

ヒロ
さっきの内積の計算で $\vec{n}\Cdot\Vec{AD}<0$ となったけど,これから分かることは?

$\vec{n}$ と $\Vec{AD}$ のなす角が鈍角ってことですか?

ヒロ
そうだね!
内積と $\vec{a},\vec{b}$ のなす角 $\theta$ の関係
$\vec{a}\Cdot\vec{b}>0$ のとき,$\theta$ は鋭角
$\vec{a}\Cdot\vec{b}=0$ のとき,$\theta$ は直角
$\vec{a}\Cdot\vec{b}<0$ のとき,$\theta$ は鈍角

ヒロ
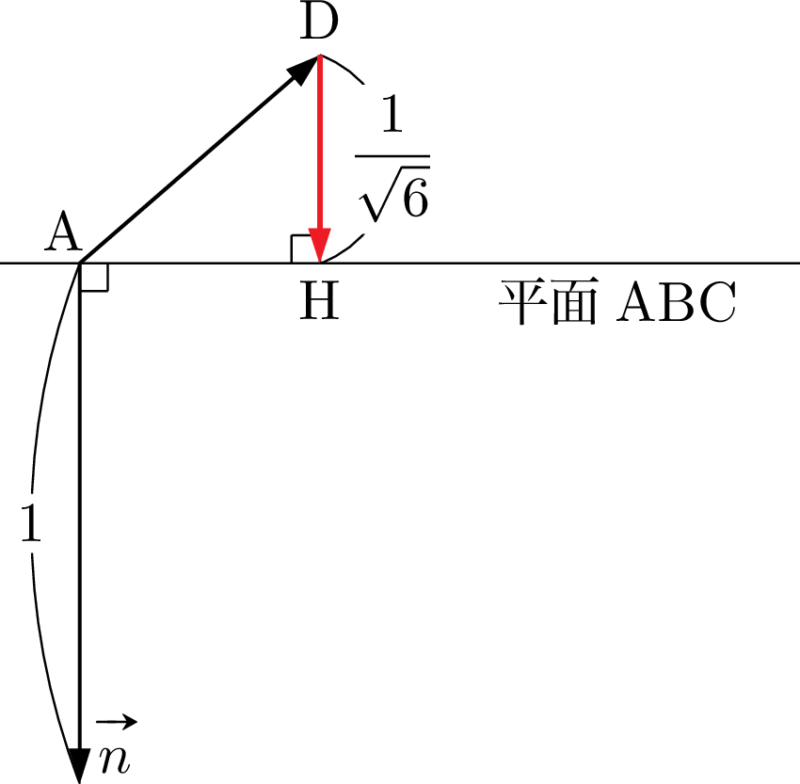
今回は内積が負だから,最初に描いた図の $\vec{n}$ の向きは,実は逆向きだったと分かるね。

なるほど!

ヒロ
あとはDHの長さが $\dfrac{1}{\sqrt6}$ ということを考えれば,$\Vec{DH}$ を求めることができるね。
\begin{align*}
\Vec{DH}&=\dfrac{1}{\sqrt{6}}\vec{n} \\[4pt]
&=\dfrac{1}{\sqrt{6}}\Cdota\dfrac{1}{\sqrt{6}}(2,-1,1) \\[4pt]
&=\left(\dfrac{1}{3},-\dfrac{1}{6},\dfrac{1}{6}\right)
\end{align*}
よって,\Vec{DH}&=\dfrac{1}{\sqrt{6}}\vec{n} \\[4pt]
&=\dfrac{1}{\sqrt{6}}\Cdota\dfrac{1}{\sqrt{6}}(2,-1,1) \\[4pt]
&=\left(\dfrac{1}{3},-\dfrac{1}{6},\dfrac{1}{6}\right)
\end{align*}
\begin{align*}
\Vec{OH}&=\Vec{OD}+\Vec{DH} \\[4pt]
&=(1,1,1)+\left(\dfrac{1}{3},-\dfrac{1}{6},\dfrac{1}{6}\right) \\[4pt]
&=\left(\dfrac{4}{3},\dfrac{5}{6},\dfrac{7}{6}\right)
\end{align*}
したがって,点Hの座標は $\left(\dfrac{4}{3},\dfrac{5}{6},\dfrac{7}{6}\right)$\Vec{OH}&=\Vec{OD}+\Vec{DH} \\[4pt]
&=(1,1,1)+\left(\dfrac{1}{3},-\dfrac{1}{6},\dfrac{1}{6}\right) \\[4pt]
&=\left(\dfrac{4}{3},\dfrac{5}{6},\dfrac{7}{6}\right)
\end{align*}

分かりました!