Contents
- ページ1
- 1 1つのベクトルの成分に0がある場合
- ページ2
- 1 垂線の足の座標
- ページ3
- 1 1つのベクトルの成分に0がない場合
- ページ4
- 1 外積の性質
- ページ5
- 1 四面体の体積
- 2 まとめ
外積の性質

ヒロ
もう少し外積について理解を深めよう。
$\vec{a}=(a_1,~a_2,~a_3),~\vec{b}=(b_1,~b_2,~b_3)$ とするとき,
\begin{align*}
\vec{a}\times\vec{b}=(a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1)
\end{align*}
外積 $\vec{a}\times\vec{b}$ と $\vec{a},~\vec{b}$ との内積を計算すると\vec{a}\times\vec{b}=(a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1)
\end{align*}
\begin{align*}
&(\vec{a}\times\vec{b})\Cdota\vec{a}
=(a_2b_3-a_3b_2)a_1+(a_3b_1-a_1b_3)a_2+(a_1b_2-a_2b_1)a_3 \\[4pt]
&={\color{red}{a_1a_2b_3}}-{\color{blue}{a_1a_3b_2}}+{\color{green}{a_2a_3b_1}} \\[4pt]
&\hspace{10ex}-{\color{red}{a_1a_2b_3}}
+{\color{blue}{a_1a_3b_2}}-{\color{green}{a_2a_3b_1}} \\[4pt]
&=0 \\[4pt]
&(\vec{a}\times\vec{b})\Cdota\vec{b}
=(a_2b_3-a_3b_2)b_1+(a_3b_1-a_1b_3)b_2+(a_1b_2-a_2b_1)b_3 \\[4pt]
&={\color{red}{a_2b_1b_3}}-{\color{blue}{a_3b_1b_2}}+{\color{blue}{a_3b_1b_2}} \\[4pt]
&\hspace{10ex}-{\color{green}{a_1b_2b_3}}
+{\color{green}{a_1b_2b_3}}-{\color{red}{a_2b_1b_3}} \\[4pt]
&=0
\end{align*}
となるから,$\vec{a}\times\vec{b}$ は $\vec{a}$ と $\vec{b}$ の両方に垂直なベクトルである。
&(\vec{a}\times\vec{b})\Cdota\vec{a}
=(a_2b_3-a_3b_2)a_1+(a_3b_1-a_1b_3)a_2+(a_1b_2-a_2b_1)a_3 \\[4pt]
&={\color{red}{a_1a_2b_3}}-{\color{blue}{a_1a_3b_2}}+{\color{green}{a_2a_3b_1}} \\[4pt]
&\hspace{10ex}-{\color{red}{a_1a_2b_3}}
+{\color{blue}{a_1a_3b_2}}-{\color{green}{a_2a_3b_1}} \\[4pt]
&=0 \\[4pt]
&(\vec{a}\times\vec{b})\Cdota\vec{b}
=(a_2b_3-a_3b_2)b_1+(a_3b_1-a_1b_3)b_2+(a_1b_2-a_2b_1)b_3 \\[4pt]
&={\color{red}{a_2b_1b_3}}-{\color{blue}{a_3b_1b_2}}+{\color{blue}{a_3b_1b_2}} \\[4pt]
&\hspace{10ex}-{\color{green}{a_1b_2b_3}}
+{\color{green}{a_1b_2b_3}}-{\color{red}{a_2b_1b_3}} \\[4pt]
&=0
\end{align*}
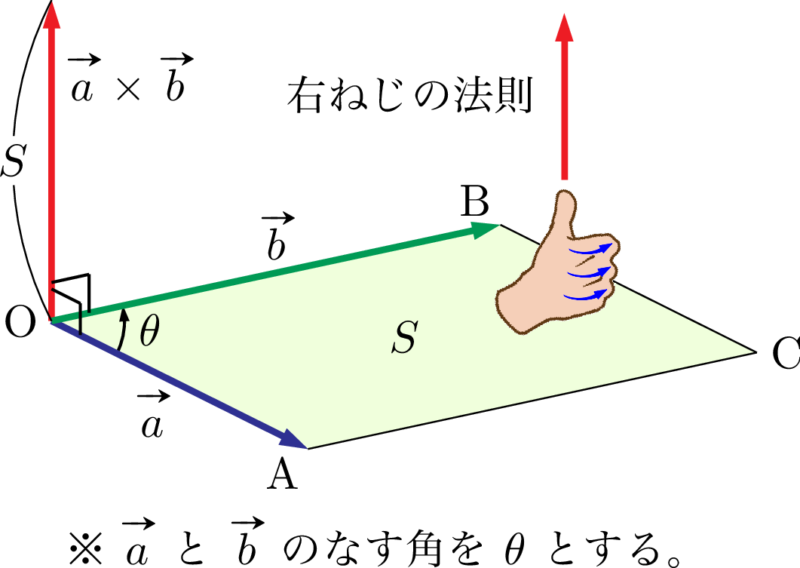
向きは右ねじの法則と同じ。つまり,$\vec{a}$ から $\vec{b}$ に右ねじを回すときに,ねじが進む方向が $\vec{a}\times\vec{b}$ の方向になる。
さらに,$\vec{a}\times\vec{b}$の大きさについて,
\begin{align*}
|\vec{a}\times\vec{b}|^2&=(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2 \\[4pt]
&=({a_1}^2+{a_2}^2+{a_3}^2)({b_1}^2+{b_2}^2+{b_3}^2)-(a_1b_1+a_2b_2+a_3b_3)^2 \\[4pt]
&=\abs{\vec{a}}^2|\vec{b}|^2-\left(\vec{a}\Cdota\vec{b}\right)^2 \\[4pt]
&=\abs{\vec{a}}^2|\vec{b}|^2
-\abs{\vec{a}}^2|\vec{b}|^2\cos^2\theta \\[4pt]
&=\abs{\vec{a}}^2|\vec{b}|^2\sin^2\theta
\end{align*}
となるから|\vec{a}\times\vec{b}|^2&=(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2 \\[4pt]
&=({a_1}^2+{a_2}^2+{a_3}^2)({b_1}^2+{b_2}^2+{b_3}^2)-(a_1b_1+a_2b_2+a_3b_3)^2 \\[4pt]
&=\abs{\vec{a}}^2|\vec{b}|^2-\left(\vec{a}\Cdota\vec{b}\right)^2 \\[4pt]
&=\abs{\vec{a}}^2|\vec{b}|^2
-\abs{\vec{a}}^2|\vec{b}|^2\cos^2\theta \\[4pt]
&=\abs{\vec{a}}^2|\vec{b}|^2\sin^2\theta
\end{align*}
\begin{align*}
|\vec{a}\times\vec{b}|=\abs{\vec{a}}|\vec{b}|\abs{\sin\theta}
\end{align*}
これは,$\vec{a}$ と $\vec{b}$ が作る平行四辺形の面積に等しいことを意味する。
|\vec{a}\times\vec{b}|=\abs{\vec{a}}|\vec{b}|\abs{\sin\theta}
\end{align*}

ということは,三角形の面積を求めるときは外積を使って検算できるってことですね!

ヒロ
お~!それを先に言うとは・・・
三角形の面積と外積の関係
\begin{align*}
\triangle\mathrm{OAB}&=\dfrac{1}{2}\abs{\vec{a}}|\vec{b}|\abs{\sin\theta} \\[4pt]
&=\dfrac{1}{2}|\vec{a}\times\vec{b}|
\end{align*}
\triangle\mathrm{OAB}&=\dfrac{1}{2}\abs{\vec{a}}|\vec{b}|\abs{\sin\theta} \\[4pt]
&=\dfrac{1}{2}|\vec{a}\times\vec{b}|
\end{align*}

ヒロ
三角形の面積の公式に外積による求め方も追加して覚えておこう。

はい!