ここでは原因の確率について解説します。
原因の確率事象 $E$ が起こる原因として,2つの事象 $A,~B$ が考えられるとき,条件付き確率 $P_E(A)$ は事象 $E$ が起こったことを知って,それが原因 $A$ から起こったと考えられる確率である。このことから $P_E(A)$ を原因の確率と呼ばれる。

ヒロ
通常は,確率では「これから起こる事象」,つまり,未来について考えます。

ヒロ
しかし,原因の確率では「既に起こった事象」,つまり,過去について考えます。このことで難しく感じるのだと思います。

ヒロ
丁寧に考えるようにしましょう。

ヒロ
実際に定期テストで出題された問題を扱って説明していきます。
原因の確率を求める問題
問題ある品物を製造するとき,A工場の製品には $5\%$,B工場の製品には $3\%$ の不良品が含まれる。A工場の製品100個とB工場の製品150個の合計250個の中から1個を取り出すとき,次の確率を求めよ。
(1) A工場の不良品である確率
(2) 不良品である確率
(3) 不良品であったとき,A工場の製品である確率
(1) A工場の不良品である確率
(2) 不良品である確率
(3) 不良品であったとき,A工場の製品である確率
【(1)の考え方と解答】
何を考えているかを明確にするためには数式を利用した方が良いため,事象を文字でおくのが良い。
今回の問題では,1個の製品を取り出すとき,その製品がA工場の製品であるという事象を $A$,B工場の製品であるという事象を $B$,不良品であるという事象を $E$ としよう。

1個の製品を取り出したときに,その製品がA工場の不良品である確率は $P(A\cap E)$ と表され,ピンクで塗った部分の確率である。
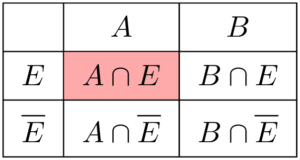
これは,A工場の製品を取り出して,その条件の下でその製品が不良品のときの確率であるから
何を考えているかを明確にするためには数式を利用した方が良いため,事象を文字でおくのが良い。
今回の問題では,1個の製品を取り出すとき,その製品がA工場の製品であるという事象を $A$,B工場の製品であるという事象を $B$,不良品であるという事象を $E$ としよう。

1個の製品を取り出したときに,その製品がA工場の不良品である確率は $P(A\cap E)$ と表され,ピンクで塗った部分の確率である。

これは,A工場の製品を取り出して,その条件の下でその製品が不良品のときの確率であるから
\begin{align*}
P(A\cap E)&=P(A)\times P_A(E) \\[4pt]&=\dfrac{100}{250}\times\dfrac{5}{100}=\dfrac{1}{50}
\end{align*}
P(A\cap E)&=P(A)\times P_A(E) \\[4pt]&=\dfrac{100}{250}\times\dfrac{5}{100}=\dfrac{1}{50}
\end{align*}
(2) 不良品である確率
【(2)の考え方と解答】
1個の製品を取り出すとき,その製品が不良品であるとき,その製品が作られた工場は,A工場・B工場の2つの場合がある。求める確率は次の表でピンクに塗った部分である。
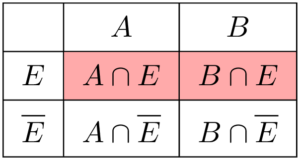
よって,求める確率は
1個の製品を取り出すとき,その製品が不良品であるとき,その製品が作られた工場は,A工場・B工場の2つの場合がある。求める確率は次の表でピンクに塗った部分である。
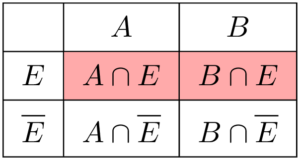
よって,求める確率は
\begin{align*}
P(E)&=P(A\cap E)+P(B\cap E) \\[4pt]&=P(A)P_A(E)+P(B)P_B(E) \\[4pt]&=\dfrac{1}{50}+\dfrac{150}{250}\Cdota\dfrac{3}{100} \\[4pt]&=\dfrac{1}{50}+\dfrac{9}{500}=\dfrac{19}{500}
\end{align*}
P(E)&=P(A\cap E)+P(B\cap E) \\[4pt]&=P(A)P_A(E)+P(B)P_B(E) \\[4pt]&=\dfrac{1}{50}+\dfrac{150}{250}\Cdota\dfrac{3}{100} \\[4pt]&=\dfrac{1}{50}+\dfrac{9}{500}=\dfrac{19}{500}
\end{align*}
(3) 不良品であったとき,A工場の製品である確率
【(3)の考え方と解答】
求める確率は,事象 $E$ を全事象と考えたときに,事象 $A$ が起こる確率である。つまり $P_E(A)$ であり
求める確率は,事象 $E$ を全事象と考えたときに,事象 $A$ が起こる確率である。つまり $P_E(A)$ であり
\begin{align*}
P_E(A)&=\dfrac{P(E\cap A)}{P(E)} \\[4pt]&=\dfrac{\dfrac{1}{50}}{\dfrac{19}{500}}=\dfrac{10}{19}
\end{align*}
P_E(A)&=\dfrac{P(E\cap A)}{P(E)} \\[4pt]&=\dfrac{\dfrac{1}{50}}{\dfrac{19}{500}}=\dfrac{10}{19}
\end{align*}
原因の確率を求める問題
問題ある電器店が,A社,B社,C社から同じ製品を仕入れた。A社,B社,C社から仕入れた比率は $5:4:3$ であり,製品が不良品である比率はそれぞれ $3\%,~4\%,~5\%$ であるという。
いま,よく混ぜられた3社の製品9900個から任意に1個抜き取って調べたところ,不良品であった。
これがA社から仕入れたものである確率を求めよ。
いま,よく混ぜられた3社の製品9900個から任意に1個抜き取って調べたところ,不良品であった。
これがA社から仕入れたものである確率を求めよ。
【考え方と解答】
9900個から任意に1個抜き取って調べたとき,その製品がA社から仕入れたものであるという事象を $A$,B社から仕入れたものであるという事象を $B$,C社から仕入れたものであるという事象を $C$,不良品であるという事象を $E$ とする。
どの部分を考えているか,また何を全体と見ているかが分かりにくい場合は,次のような表を書いて思考を整理しよう。

求める確率は $P_E(A)$ であり
9900個から任意に1個抜き取って調べたとき,その製品がA社から仕入れたものであるという事象を $A$,B社から仕入れたものであるという事象を $B$,C社から仕入れたものであるという事象を $C$,不良品であるという事象を $E$ とする。
どの部分を考えているか,また何を全体と見ているかが分かりにくい場合は,次のような表を書いて思考を整理しよう。

求める確率は $P_E(A)$ であり
\begin{align*}
P_E(A)=\dfrac{P(A\cap E)}{P(E)}
\end{align*}
で求められる。ここで,与えられた条件よりP_E(A)=\dfrac{P(A\cap E)}{P(E)}
\end{align*}
\begin{align*}
&P(A)=\dfrac{5}{5+4+3}=\dfrac{5}{12} \\[4pt]&P(B)=\dfrac{4}{5+4+3}=\dfrac{4}{12} \\[4pt]&P(C)=\dfrac{3}{5+4+3}=\dfrac{3}{12} \\[4pt]&P_A(E)=\dfrac{3}{100} \\[4pt]&P_B(E)=\dfrac{4}{100} \\[4pt]&P_C(E)=\dfrac{5}{100}
\end{align*}
となるから,$P(E)$ は&P(A)=\dfrac{5}{5+4+3}=\dfrac{5}{12} \\[4pt]&P(B)=\dfrac{4}{5+4+3}=\dfrac{4}{12} \\[4pt]&P(C)=\dfrac{3}{5+4+3}=\dfrac{3}{12} \\[4pt]&P_A(E)=\dfrac{3}{100} \\[4pt]&P_B(E)=\dfrac{4}{100} \\[4pt]&P_C(E)=\dfrac{5}{100}
\end{align*}
\begin{align*}
P(E)&=P(A\cap E)+P(B\cap E)+P(C\cap E) \\[4pt]&=P(A)P_A(E)+P(B)P_B(E)+P(C)P_C(E) \\[4pt]&=\dfrac{5}{12}\Cdota\dfrac{3}{100}+\dfrac{4}{12}\Cdota\dfrac{4}{100}+\dfrac{3}{12}\Cdota\dfrac{5}{100} \\[4pt]&=\dfrac{15+16+15}{1200}=\dfrac{46}{1200}
\end{align*}
したがって,求める確率はP(E)&=P(A\cap E)+P(B\cap E)+P(C\cap E) \\[4pt]&=P(A)P_A(E)+P(B)P_B(E)+P(C)P_C(E) \\[4pt]&=\dfrac{5}{12}\Cdota\dfrac{3}{100}+\dfrac{4}{12}\Cdota\dfrac{4}{100}+\dfrac{3}{12}\Cdota\dfrac{5}{100} \\[4pt]&=\dfrac{15+16+15}{1200}=\dfrac{46}{1200}
\end{align*}
\begin{align*}
P_E(A)&=\dfrac{P(A\cap E)}{P(E)} \\[4pt]&=\dfrac{\dfrac{15}{1200}}{\dfrac{46}{1200}}=\dfrac{15}{46}
\end{align*}
P_E(A)&=\dfrac{P(A\cap E)}{P(E)} \\[4pt]&=\dfrac{\dfrac{15}{1200}}{\dfrac{46}{1200}}=\dfrac{15}{46}
\end{align*}

ヒロ
「9900個」という具体的な個数が与えられているが,それに惑わされないようにしよう。
よく目にする入試問題
1976年 早稲田大5回に1回の割合で帽子を忘れるくせのあるK君が,正月にA, B, C3軒を順に年始回りをして家に帰ったところ,この3軒のいずれかに帽子を忘れてきたことに気が付いた。2件目の家Bに忘れてきた確率を求めよ。
【考え方と解答】
家A, B, Cに帽子を忘れる確率をそれぞれ $P(A)$, $P(B)$, $P(C)$ とすると,$P(A)$ は5回に1回の割合で帽子を忘れることから
家A, B, Cに帽子を忘れる確率をそれぞれ $P(A)$, $P(B)$, $P(C)$ とすると,$P(A)$ は5回に1回の割合で帽子を忘れることから
\begin{align*}
P(A)=\dfrac{1}{5}
\end{align*}
$P(B)$ は家Aで帽子を忘れないで,家Bで帽子を忘れる確率だからP(A)=\dfrac{1}{5}
\end{align*}
\begin{align*}
P(B)&=\left(1-\dfrac{1}{5}\right)\Cdota\dfrac{1}{5} \\[4pt]
&=\dfrac{4}{5}\Cdota\dfrac{1}{5}=\dfrac{4}{25}
\end{align*}
$P(C)$ は家A, Bで帽子を忘れないで,家Cで帽子を忘れる確率だからP(B)&=\left(1-\dfrac{1}{5}\right)\Cdota\dfrac{1}{5} \\[4pt]
&=\dfrac{4}{5}\Cdota\dfrac{1}{5}=\dfrac{4}{25}
\end{align*}
\begin{align*}
P(C)&=\left(1-\dfrac{1}{5}\right)^2\Cdota\dfrac{1}{5} \\[4pt]
&=\dfrac{16}{25}\Cdota\dfrac{1}{5}=\dfrac{16}{125}
\end{align*}
したがって,3軒のいずれかに帽子を忘れる確率 $P(F)$ はP(C)&=\left(1-\dfrac{1}{5}\right)^2\Cdota\dfrac{1}{5} \\[4pt]
&=\dfrac{16}{25}\Cdota\dfrac{1}{5}=\dfrac{16}{125}
\end{align*}
\begin{align*}
P(F)&=P(A)+P(B)+P(C)=\dfrac{1}{5}+\dfrac{4}{25}+\dfrac{16}{125} \\[4pt]
&=\dfrac{25+20+16}{125}=\dfrac{61}{125}
\end{align*}
よって,3軒のいずれかに帽子を忘れたときに,家Bに忘れてきた条件付き確率はP(F)&=P(A)+P(B)+P(C)=\dfrac{1}{5}+\dfrac{4}{25}+\dfrac{16}{125} \\[4pt]
&=\dfrac{25+20+16}{125}=\dfrac{61}{125}
\end{align*}
\begin{align*}
P_F(B)&=\dfrac{P(B)}{P(F)} \\[4pt]
&=\dfrac{\dfrac{4}{25}}{\dfrac{61}{125}}=\dfrac{20}{61}
\end{align*}
P_F(B)&=\dfrac{P(B)}{P(F)} \\[4pt]
&=\dfrac{\dfrac{4}{25}}{\dfrac{61}{125}}=\dfrac{20}{61}
\end{align*}



















