ここでは正弦定理と余弦定理を利用して様々な問題を解く方法について説明します。
三角形の辺の長さや角の大きさを求めるためには,正弦定理や余弦定理をうまく使えるようになる必要があります。
問題によっては片方だけでは解けない問題もあります。
状況に応じて対応できる力を身に付けましょう。
Contents
測量の問題(平面)
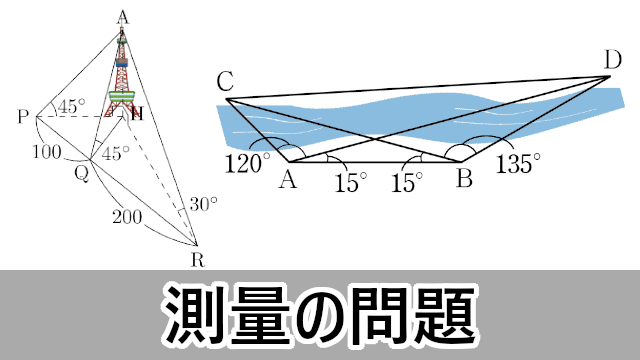
問題川の向こうにある2地点C, D間の距離を求めるために,2地点A, Bにおいて,$\kaku{BAD}$, $\kaku{DAC}$, $\kaku{ABC}$, $\kaku{CBD}$ を測ったところ図のような値が得られた。
$\text{AB}=1$ kmのとき,C, D間の距離を求めよ。
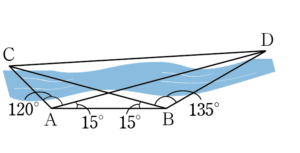
$\text{AB}=1$ kmのとき,C, D間の距離を求めよ。


ヒロ
図形問題を考えるときは,次のポイントを意識しよう。
図形問題の考え方辺の長さや角の大きさ求めたいときは,その辺や角を含む三角形を探す。
【考え方と解答】
求めたいのはCDの長さだから,$\sankaku{ACD}$ や $\sankaku{BCD}$ に着目する。$\sankaku{ACD}$ に着目した場合はACとADの長さを求めてから余弦定理でCDを求めることになる。$\sankaku{BCD}$ に着目した場合はBCとBDの長さを求めてから余弦定理でCDを求めることになる。ACとAD,BCとBDのどちらを求めるのが簡単かによって着目する三角形は変わる。ただ,それも考えてみないことには分からないため,とりあえずそれら4つの辺の長さを求めようと考えてみれば良い。
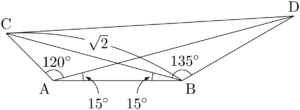
ABの長さが分かっているから,その対角の大きさによって着目する三角形を決めよう。$\kaku{ACB}=30\Deg$,$\kaku{ADB}=15\Deg$ であるから$\sankaku{ABC}$ に着目してみよう。正弦定理より
$\sankaku{ABD}$に着目すると $\kaku{BAD}=15\Deg$, $\kaku{ABD}=150\Deg$ であるから,$\kaku{BDA}=15\Deg$ となる。よって,$\sankaku{ABD}$ は底角が等しい三角形であるから二等辺三角形である。したがって,$\text{BD}=\text{AB}=1$ である。

これで $\sankaku{BCD}$ に着目することによってCDの長さを求めることができる。
余弦定理より
求めたいのはCDの長さだから,$\sankaku{ACD}$ や $\sankaku{BCD}$ に着目する。$\sankaku{ACD}$ に着目した場合はACとADの長さを求めてから余弦定理でCDを求めることになる。$\sankaku{BCD}$ に着目した場合はBCとBDの長さを求めてから余弦定理でCDを求めることになる。ACとAD,BCとBDのどちらを求めるのが簡単かによって着目する三角形は変わる。ただ,それも考えてみないことには分からないため,とりあえずそれら4つの辺の長さを求めようと考えてみれば良い。
ABの長さが分かっているから,その対角の大きさによって着目する三角形を決めよう。$\kaku{ACB}=30\Deg$,$\kaku{ADB}=15\Deg$ であるから$\sankaku{ABC}$ に着目してみよう。正弦定理より
\begin{align*}
&\dfrac{\text{AB}}{\sin\kaku{ACB}}=\dfrac{\text{BC}}{\kaku{BAC}} \\[4pt]&\text{BC}=\dfrac{\sin\kaku{BAC}}{\sin\kaku{ACB}}\text{AB}
\end{align*}
よって&\dfrac{\text{AB}}{\sin\kaku{ACB}}=\dfrac{\text{BC}}{\kaku{BAC}} \\[4pt]&\text{BC}=\dfrac{\sin\kaku{BAC}}{\sin\kaku{ACB}}\text{AB}
\end{align*}
\begin{align*}
\text{BC}&=\dfrac{\sin135\Deg}{\sin30\Deg} \\[4pt]&=\dfrac{\sqrt{2}}{2}\Cdota2=\sqrt{2}
\end{align*}
\text{BC}&=\dfrac{\sin135\Deg}{\sin30\Deg} \\[4pt]&=\dfrac{\sqrt{2}}{2}\Cdota2=\sqrt{2}
\end{align*}

$\sankaku{ABD}$に着目すると $\kaku{BAD}=15\Deg$, $\kaku{ABD}=150\Deg$ であるから,$\kaku{BDA}=15\Deg$ となる。よって,$\sankaku{ABD}$ は底角が等しい三角形であるから二等辺三角形である。したがって,$\text{BD}=\text{AB}=1$ である。

これで $\sankaku{BCD}$ に着目することによってCDの長さを求めることができる。
余弦定理より
\begin{align*}
\text{CD}^2&=\text{BC}^2+\text{BD}^2-2\text{BC}\Cdota\text{BD}\cos\kaku{CBD} \\[4pt]&=(\sqrt{2})^2+1^2-2\sqrt{2}\Cdota1\Cdota\cos135\Deg \\[4pt]&=3-2\sqrt{2}\Cdota\left(-\dfrac{1}{\sqrt{2}}\right) \\[4pt]&=5
\end{align*}
$\text{CD}>0$ より $\text{CD}=\sqrt{5}$\text{CD}^2&=\text{BC}^2+\text{BD}^2-2\text{BC}\Cdota\text{BD}\cos\kaku{CBD} \\[4pt]&=(\sqrt{2})^2+1^2-2\sqrt{2}\Cdota1\Cdota\cos135\Deg \\[4pt]&=3-2\sqrt{2}\Cdota\left(-\dfrac{1}{\sqrt{2}}\right) \\[4pt]&=5
\end{align*}
測量の問題(空間)
問題図において塔AHは,H,P,Q,Rを含む平面に垂直に立っている。
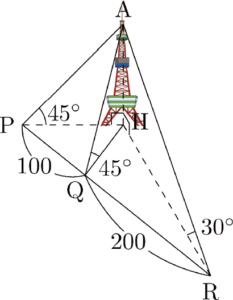
P,Q,Rはこの順に一直線上にあり $\text{PQ}=100$ m, $\text{QR}=200$ mである。塔AHの高さを求めるためにP,Q,Rの3点から点Aを
見上げたところ $\kaku{APH}=\kaku{AQH}=45\Deg,~\kaku{ARH}=30\Deg$ であった。
塔AHの高さを $x$ mとおいたとき,以下の問いに答えなさい。
(1) HRを $x$ を用いて表せ。
(2) $\cos\kaku{PQH}$ を $x$ を用いて表せ。
(3) $x$ の値を求めよ。

P,Q,Rはこの順に一直線上にあり $\text{PQ}=100$ m, $\text{QR}=200$ mである。塔AHの高さを求めるためにP,Q,Rの3点から点Aを
見上げたところ $\kaku{APH}=\kaku{AQH}=45\Deg,~\kaku{ARH}=30\Deg$ であった。
塔AHの高さを $x$ mとおいたとき,以下の問いに答えなさい。
(1) HRを $x$ を用いて表せ。
(2) $\cos\kaku{PQH}$ を $x$ を用いて表せ。
(3) $x$ の値を求めよ。

ヒロ
空間の問題では,立体的に見た図のまま考えるのではなく,真正面から見た図を考えるようにしよう。

ヒロ
また,想像して解くのが難しい場合は,手間でも丁寧に図を描くようにしよう。
【(1)の考え方と解答】
HRを含む三角形を探すと $\sankaku{AHR}$ が見つかる。
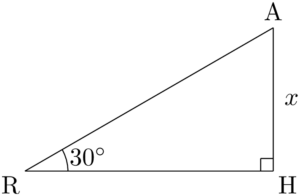
$\sankaku{ARH}$ において,$\tan30\Deg=\dfrac{\text{AH}}{\text{HR}}$だから,
HRを含む三角形を探すと $\sankaku{AHR}$ が見つかる。

$\sankaku{ARH}$ において,$\tan30\Deg=\dfrac{\text{AH}}{\text{HR}}$だから,
\begin{align*}
&\dfrac{x}{\text{HR}}=\dfrac{1}{\sqrt3} \\[4pt]&\text{HR}=\sqrt3x
\end{align*}
&\dfrac{x}{\text{HR}}=\dfrac{1}{\sqrt3} \\[4pt]&\text{HR}=\sqrt3x
\end{align*}
(2) $\cos\kaku{PQH}$を$x$を用いて表せ。
【(2)の考え方と解答】
$\kaku{PQH}$ を含む三角形を探すと,$\sankaku{PQH}$ が見つかる。
まず,PHとQHの長さを求めよう。そのためにそれぞれの辺を含む別の三角形に着目する。
PHを含む三角形を探すと $\sankaku{APH}$ が見つかる。またQHを含む三角形を探すと $\sankaku{AQH}$ が見つかる。2地点P, QからAを見上げた仰角が45°で等しく,AHが共通な辺だから2つの三角形は合同な直角二等辺三角形である。したがって,PHとQHはAHと長さが等しく,$\text{PH}=\text{QH}=x$だから,$\sankaku{PQH}$は二等辺三角形である。
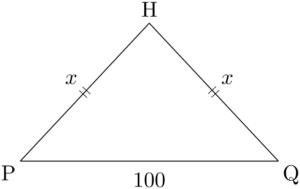
$\sankaku{PQH}$ は二等辺三角形であるから,PQの中点をMとするとMHとPQは垂直になる。
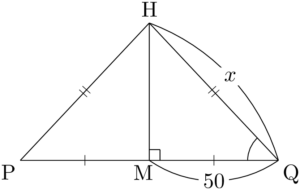
よって,
$\kaku{PQH}$ を含む三角形を探すと,$\sankaku{PQH}$ が見つかる。
まず,PHとQHの長さを求めよう。そのためにそれぞれの辺を含む別の三角形に着目する。
PHを含む三角形を探すと $\sankaku{APH}$ が見つかる。またQHを含む三角形を探すと $\sankaku{AQH}$ が見つかる。2地点P, QからAを見上げた仰角が45°で等しく,AHが共通な辺だから2つの三角形は合同な直角二等辺三角形である。したがって,PHとQHはAHと長さが等しく,$\text{PH}=\text{QH}=x$だから,$\sankaku{PQH}$は二等辺三角形である。

$\sankaku{PQH}$ は二等辺三角形であるから,PQの中点をMとするとMHとPQは垂直になる。

よって,
\begin{align*}
\cos\kaku{PQH}=\dfrac{\dfrac{1}{2}\text{PQ}}{\text{QH}}=\dfrac{50}{x}
\end{align*}
\cos\kaku{PQH}=\dfrac{\dfrac{1}{2}\text{PQ}}{\text{QH}}=\dfrac{50}{x}
\end{align*}

ヒロ
二等辺三角形の底角のコサインの値を求めるときは,余弦定理を使う必要がないことを知っておこう。
二等辺三角形の底角のコサイン次の図のような二等辺三角形ABCにおいて,$\cos\kaku{ABC}$ を求めることを考える。
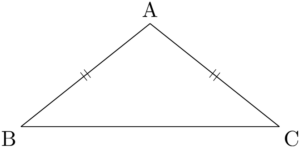
頂点Aから辺BCに垂線AHを引くと,HはBCの中点になる。
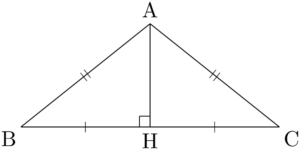
$\sankaku{ABH}$ が直角三角形になるから,

頂点Aから辺BCに垂線AHを引くと,HはBCの中点になる。

$\sankaku{ABH}$ が直角三角形になるから,
\begin{align*}
\cos\kaku{ABC}&=\dfrac{\text{BH}}{\text{AB}}=\dfrac{\dfrac{1}{2}\text{BC}}{\text{AB}}
\end{align*}
\cos\kaku{ABC}&=\dfrac{\text{BH}}{\text{AB}}=\dfrac{\dfrac{1}{2}\text{BC}}{\text{AB}}
\end{align*}
(3) $x$ の値を求めよ。
【(3)の考え方と解答】
$x$ を求めるために,方程式を立てよう。
(2)で求めた $\cos\kaku{PQH}$ を利用することを考えよう。と言っても,そのまま $\sankaku{PQH}$ に着目しても意味がないから,$\kaku{PQH}$ を外角にもつ $\sankaku{QRH}$ に着目してみよう。
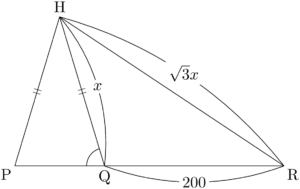
$\kaku{RQH}=180\Deg-\kaku{PQH}$ であるから,
$x$ を求めるために,方程式を立てよう。
(2)で求めた $\cos\kaku{PQH}$ を利用することを考えよう。と言っても,そのまま $\sankaku{PQH}$ に着目しても意味がないから,$\kaku{PQH}$ を外角にもつ $\sankaku{QRH}$ に着目してみよう。

$\kaku{RQH}=180\Deg-\kaku{PQH}$ であるから,
\begin{align*}
\cos\kaku{RQH}&=\cos(180\Deg-\kaku{PQH}) \\[4pt]&=-\cos\kaku{PQH}=-\dfrac{50}{x}
\end{align*}
となる。$\sankaku{QRH}$ において,余弦定理を用いると,\cos\kaku{RQH}&=\cos(180\Deg-\kaku{PQH}) \\[4pt]&=-\cos\kaku{PQH}=-\dfrac{50}{x}
\end{align*}
\begin{align*}
&\text{HR}^2=\text{QR}^2+\text{QH}^2-2\Cdota\text{QR}\Cdota\text{QH}\cos\kaku{RQH} \\
&(\sqrt3x)^2=200^2+x^2-2\Cdota200x\Cdota\left(-\dfrac{50}{x}\right) \\
&3x^2=40000+x^2+20000 \\
&x^2=30000
\end{align*}
$x>0$ より $x=100\sqrt3$&\text{HR}^2=\text{QR}^2+\text{QH}^2-2\Cdota\text{QR}\Cdota\text{QH}\cos\kaku{RQH} \\
&(\sqrt3x)^2=200^2+x^2-2\Cdota200x\Cdota\left(-\dfrac{50}{x}\right) \\
&3x^2=40000+x^2+20000 \\
&x^2=30000
\end{align*}