三角比を利用して空間図形の問題を解く問題について説明します。
【数学IA】空間図形の応用問題【広島工業大・東京慈恵会医科大】
ここでは三角比を利用して空間図形の問題を解く方法について説明します。 問題に出てくる空間図形として,直方体・立方体・三角錐(四面体)・球・円錐などがあります。 どのような空間図形であっても,平面で切断したときに現れる切断面を捉えて,平面図形...

【数学IA】空間図形の応用問題【茨城大・大阪市立大】
前回に引き続き,三角比を利用して空間図形の問題を解く方法について説明します。 空間図形の問題では,体積を求める問題が多く出題されるため,様々な問題を解いて慣れておくことが重要です。 平面図形の問題として考える部分と,空間図形の問題として考え...
空間図形の問題を初見で解くためには,基本的な考え方を身に付けておくことが重要です。
様々な問題を解いて知識と経験を蓄積しましょう。
Contents
四面体と球の問題

ヒロ
四面体と球に関する問題が関東学院大で出題されている。

ヒロ
改題としているものの,解答のハコの部分についてのみ記述を変えているだけで内容は元の問題と同じである。
2016年 関東学院大・改題以下の $\myhako$ を埋めよ。ただし,分数は可能な限り約分した形で答えること。また,根号の中に現れる自然数は,最小となる形で答えること。
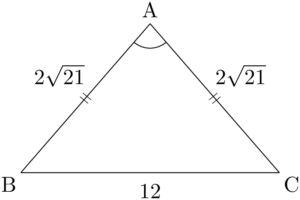
四面体ABCDがあり,辺の長さは $\text{AB}=\text{AC}=\text{AD}=2\sqrt{21}$, $\text{BC}=\text{CD}=\text{DB}=12$ である。以下の問に答えよ。
(1) $\cos\kaku{BAC}=\dfrac{\myhako}{\myhako}$
(2) 三角形ABCの面積は $\myhako\sqrt{\myhako}$
(3) 三角形ABCを含む平面の中で,三角形ABCの外接円を考えると,その半径は $\dfrac{\myhako\sqrt{\myhako}}{\myhako}$
(4) 四面体ABCDの体積は $\myhako\sqrt{\myhako}$
(5) 四面体ABCDに内接する球を考えると,この球の体積は $\dfrac{\myhako\sqrt{\myhako}}{\myhako}\pi$
四面体ABCDがあり,辺の長さは $\text{AB}=\text{AC}=\text{AD}=2\sqrt{21}$, $\text{BC}=\text{CD}=\text{DB}=12$ である。以下の問に答えよ。
(1) $\cos\kaku{BAC}=\dfrac{\myhako}{\myhako}$
(2) 三角形ABCの面積は $\myhako\sqrt{\myhako}$
(3) 三角形ABCを含む平面の中で,三角形ABCの外接円を考えると,その半径は $\dfrac{\myhako\sqrt{\myhako}}{\myhako}$
(4) 四面体ABCDの体積は $\myhako\sqrt{\myhako}$
(5) 四面体ABCDに内接する球を考えると,この球の体積は $\dfrac{\myhako\sqrt{\myhako}}{\myhako}\pi$
【(1)の考え方と解答】
$\sankaku{ABC}$ に着目して余弦定理で求めよう。
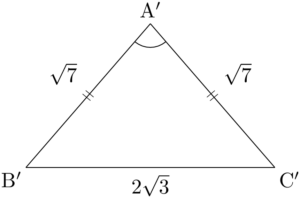
このまま余弦定理を使っても良いが,数字が大きいので小さくすると計算が楽になる。例えば3辺の長さをすべて半分にしても,3つの内角は変わらず,長さだけが半分になった $\sankaku{ABC}$ と相似な三角形になるから $\cos\kaku{BAC}$ の値も変わらない。今回は $12=(2\sqrt{3})^2$ であることを考えて $2\sqrt{3}$ で割った $\sankaku{A’B’C’}$ を考える。
$\sankaku{ABC}$ に着目して余弦定理で求めよう。

このまま余弦定理を使っても良いが,数字が大きいので小さくすると計算が楽になる。例えば3辺の長さをすべて半分にしても,3つの内角は変わらず,長さだけが半分になった $\sankaku{ABC}$ と相似な三角形になるから $\cos\kaku{BAC}$ の値も変わらない。今回は $12=(2\sqrt{3})^2$ であることを考えて $2\sqrt{3}$ で割った $\sankaku{A’B’C’}$ を考える。

\begin{align*}
\cos\kaku{BAC}&=\dfrac{(\sqrt{7})^2+(\sqrt{7})^2-(2\sqrt{3})^2}{2\sqrt{7}\Cdot\sqrt{7}} \\[4pt]&=\dfrac{2}{14}=\dfrac{1}{7}
\end{align*}
\cos\kaku{BAC}&=\dfrac{(\sqrt{7})^2+(\sqrt{7})^2-(2\sqrt{3})^2}{2\sqrt{7}\Cdot\sqrt{7}} \\[4pt]&=\dfrac{2}{14}=\dfrac{1}{7}
\end{align*}
(2) 三角形ABCの面積は $\myhako\sqrt{\myhako}$
【(2)の考え方と解答】
(1)で求めた $\cos\kaku{BAC}$ の値から $\sin\kaku{BAC}$ の値を求めよう。
$\sin\kaku{BAC}>0$ であるから
(1)で求めた $\cos\kaku{BAC}$ の値から $\sin\kaku{BAC}$ の値を求めよう。
$\sin\kaku{BAC}>0$ であるから
\begin{align*}
\sin\kaku{BAC}&=\sqrt{1-\cos^2\kaku{BAC}} \\[4pt]&=\sqrt{1-\left(\dfrac{1}{7}\right)^2} \\[4pt]&=\dfrac{4\sqrt{3}}{7}
\end{align*}
よって\sin\kaku{BAC}&=\sqrt{1-\cos^2\kaku{BAC}} \\[4pt]&=\sqrt{1-\left(\dfrac{1}{7}\right)^2} \\[4pt]&=\dfrac{4\sqrt{3}}{7}
\end{align*}
\begin{align*}
\sankaku{ABC}&=\dfrac{1}{2}\text{AB}\Cdota\text{AC}\sin\kaku{BAC} \\[4pt]&=\dfrac{1}{2}\Cdota(2\sqrt{21})^2\Cdota\dfrac{4\sqrt{3}}{7} \\[4pt]&=24\sqrt{3}
\end{align*}
\sankaku{ABC}&=\dfrac{1}{2}\text{AB}\Cdota\text{AC}\sin\kaku{BAC} \\[4pt]&=\dfrac{1}{2}\Cdota(2\sqrt{21})^2\Cdota\dfrac{4\sqrt{3}}{7} \\[4pt]&=24\sqrt{3}
\end{align*}

ヒロ
$\sankaku{ABC}$ は二等辺三角形だから,簡単に高さを求めることができる。次のようにして解く人もいるだろう。
【(2)の別解】
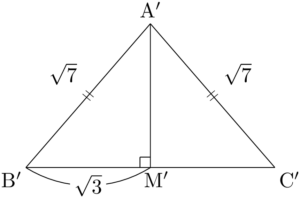
点Aから辺BCに垂線AMを下ろすと,MはBCの中点になる。次の図は数値を小さくするために $2\sqrt{3}$ で割ったものである。また,Mに対応する点をM$’$ としている。
三平方の定理より
点Aから辺BCに垂線AMを下ろすと,MはBCの中点になる。次の図は数値を小さくするために $2\sqrt{3}$ で割ったものである。また,Mに対応する点をM$’$ としている。

三平方の定理より
\begin{align*}
\text{AM}&=2\sqrt{3}\text{A$’$M$’$} \\[4pt]&=2\sqrt{3}\sqrt{(\sqrt{7})^2-(\sqrt{3})^2} \\[4pt]&=4\sqrt{3}
\end{align*}
となるから\text{AM}&=2\sqrt{3}\text{A$’$M$’$} \\[4pt]&=2\sqrt{3}\sqrt{(\sqrt{7})^2-(\sqrt{3})^2} \\[4pt]&=4\sqrt{3}
\end{align*}
\begin{align*}
\sankaku{ABC}&=\dfrac{1}{2}\text{BC}\Cdota\text{AM} \\[4pt]&=\dfrac{1}{2}\Cdota12\Cdota4\sqrt{3} \\[4pt]&=24\sqrt{3}
\end{align*}
\sankaku{ABC}&=\dfrac{1}{2}\text{BC}\Cdota\text{AM} \\[4pt]&=\dfrac{1}{2}\Cdota12\Cdota4\sqrt{3} \\[4pt]&=24\sqrt{3}
\end{align*}
(3) 三角形ABCを含む平面の中で,三角形ABCの外接円を考えると,その半径は $\dfrac{\myhako\sqrt{\myhako}}{\myhako}$
【(3)の考え方と解答】
外接円の半径を求める基本的な方法は正弦定理を利用することだね。求める半径を $R$ とすると
外接円の半径を求める基本的な方法は正弦定理を利用することだね。求める半径を $R$ とすると
\begin{align*}
R&=\dfrac{\text{BC}}{2\sin\kaku{BAC}} \\[4pt]&=\dfrac{12}{2\Cdot\dfrac{4\sqrt{3}}{7}} \\[4pt]&=\dfrac{21}{2\sqrt{3}}=\dfrac{7\sqrt{3}}{2}
\end{align*}
R&=\dfrac{\text{BC}}{2\sin\kaku{BAC}} \\[4pt]&=\dfrac{12}{2\Cdot\dfrac{4\sqrt{3}}{7}} \\[4pt]&=\dfrac{21}{2\sqrt{3}}=\dfrac{7\sqrt{3}}{2}
\end{align*}
(4) 四面体ABCDの体積は $\myhako\sqrt{\myhako}$
【(4)の考え方と解答】
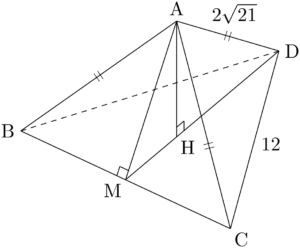
点Aから面BCDに垂線AHを下ろしてAHの長さを求めよう。$\text{AB}=\text{AC}=\text{AD}$ であるから,Hは $\sankaku{BCD}$ の外心である。
正三角形BCDにおいて,正弦定理より
点Aから面BCDに垂線AHを下ろしてAHの長さを求めよう。$\text{AB}=\text{AC}=\text{AD}$ であるから,Hは $\sankaku{BCD}$ の外心である。

正三角形BCDにおいて,正弦定理より
\begin{align*}
\text{DH}&=\dfrac{12}{2\sin60\Deg} \\[4pt]&=\dfrac{12}{\sqrt{3}}=4\sqrt{3}
\end{align*}
$\sankaku{ADH}$ において,三平方の定理より\text{DH}&=\dfrac{12}{2\sin60\Deg} \\[4pt]&=\dfrac{12}{\sqrt{3}}=4\sqrt{3}
\end{align*}
\begin{align*}
\text{AH}&=\sqrt{\text{AD}^2-\text{DH}^2} \\[4pt]&=\sqrt{(2\sqrt{21})^2-(4\sqrt{3})^2} \\[4pt]&=\sqrt{84-48}=\sqrt{36} \\[4pt]&=6
\end{align*}
$\sankaku{BCD}$ は1辺の長さが12の正三角形であるから,その面積は\text{AH}&=\sqrt{\text{AD}^2-\text{DH}^2} \\[4pt]&=\sqrt{(2\sqrt{21})^2-(4\sqrt{3})^2} \\[4pt]&=\sqrt{84-48}=\sqrt{36} \\[4pt]&=6
\end{align*}
\begin{align*}
\sankaku{BCD}&=\dfrac{\sqrt{3}}{4}\Cdota12^2 \\[4pt]&=36\sqrt{3}
\end{align*}
よって,求める体積を $V_1$ とすると\sankaku{BCD}&=\dfrac{\sqrt{3}}{4}\Cdota12^2 \\[4pt]&=36\sqrt{3}
\end{align*}
\begin{align*}
V_1&=\dfrac{1}{3}\sankaku{BCD}\Cdota\text{AH} \\[4pt]&=\dfrac{1}{3}\Cdota36\sqrt{3}\Cdota6 \\[4pt]&=72\sqrt{3}
\end{align*}
V_1&=\dfrac{1}{3}\sankaku{BCD}\Cdota\text{AH} \\[4pt]&=\dfrac{1}{3}\Cdota36\sqrt{3}\Cdota6 \\[4pt]&=72\sqrt{3}
\end{align*}
(5) 四面体ABCDに内接する球を考えると,この球の体積は $\dfrac{\myhako\sqrt{\myhako}}{\myhako}\pi$
【(5)の考え方と解答】
球の体積を求めるために,球の半径を求めよう。四面体ABCDに内接する球を描くと次のようになる。
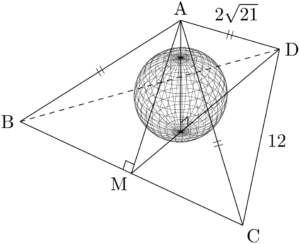
実際に描くのは難しいが,想像するのはできるだろう。ただ,正確に想像できなくても問題を解くことはできる。球が四面体に内接するとき,その球は4つの面すべてと接する。したがって,球の中心をIとして,Iと4つの頂点A, B, C, Dを結ぶと,4つの三角錐に分割できることが分かる。
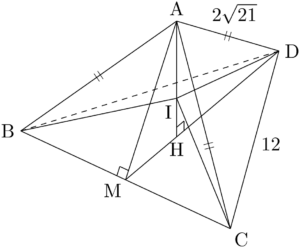
球は四面体ABCDに内接しているから,4つの三角錐IABC, IACD, IABD, IBCDの高さはすべて等しい。(4)で四面体ABCDの体積を求めたから,4つの三角錐の高さ,すなわち内接球の半径を求めることができるね。内接球の半径を $r$ とすると
球の体積を求めるために,球の半径を求めよう。四面体ABCDに内接する球を描くと次のようになる。

実際に描くのは難しいが,想像するのはできるだろう。ただ,正確に想像できなくても問題を解くことはできる。球が四面体に内接するとき,その球は4つの面すべてと接する。したがって,球の中心をIとして,Iと4つの頂点A, B, C, Dを結ぶと,4つの三角錐に分割できることが分かる。

球は四面体ABCDに内接しているから,4つの三角錐IABC, IACD, IABD, IBCDの高さはすべて等しい。(4)で四面体ABCDの体積を求めたから,4つの三角錐の高さ,すなわち内接球の半径を求めることができるね。内接球の半径を $r$ とすると
\begin{align*}
&V=\dfrac{1}{3}\sankaku{ABC}\Cdota r+\dfrac{1}{3}\sankaku{ACD}\Cdota r+\dfrac{1}{3}\sankaku{ABD}\Cdota r+\dfrac{1}{3}\sankaku{BCD}\Cdota r
\end{align*}
が成り立つ。ここで(2)の結果より&V=\dfrac{1}{3}\sankaku{ABC}\Cdota r+\dfrac{1}{3}\sankaku{ACD}\Cdota r+\dfrac{1}{3}\sankaku{ABD}\Cdota r+\dfrac{1}{3}\sankaku{BCD}\Cdota r
\end{align*}
\begin{align*}
\sankaku{ABC}=\sankaku{ACD}=\sankaku{ABD}=24\sqrt{3}
\end{align*}
であり,(4)より $\sankaku{BCD}=36\sqrt{3}$ であるから\sankaku{ABC}=\sankaku{ACD}=\sankaku{ABD}=24\sqrt{3}
\end{align*}
\begin{align*}
V&=\dfrac{1}{3}\Cdota24\sqrt{3}r\times3+\dfrac{1}{3}\Cdota36\sqrt{3}r \\[4pt]&=36\sqrt{3}r
\end{align*}
(4)の結果よりV&=\dfrac{1}{3}\Cdota24\sqrt{3}r\times3+\dfrac{1}{3}\Cdota36\sqrt{3}r \\[4pt]&=36\sqrt{3}r
\end{align*}
\begin{align*}
&36\sqrt{3}r=72\sqrt{3} \\[4pt]&r=2
\end{align*}
よって,求める球の体積を $V_2$ とすると&36\sqrt{3}r=72\sqrt{3} \\[4pt]&r=2
\end{align*}
\begin{align*}
V_2&=\dfrac{4}{3}\pi r^3 \\[4pt]&=\dfrac{4}{3}\pi\Cdota2^3=\dfrac{32}{3}\pi
\end{align*}
V_2&=\dfrac{4}{3}\pi r^3 \\[4pt]&=\dfrac{4}{3}\pi\Cdota2^3=\dfrac{32}{3}\pi
\end{align*}

ヒロ
また,次のような解法で解いた人もいるだろう。
【(5)の別解】
四面体ABCDを平面ADMで切った断面を考えると,内接球の中心IはAh上にあり,面ABCとの接点をTとすると点TはAM上にある。
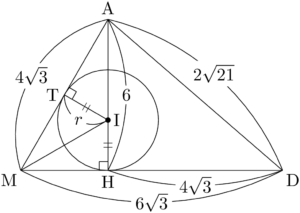
$\text{DM}=6\sqrt{3}$, $\text{DH}=4\sqrt{3}$ より,
四面体ABCDを平面ADMで切った断面を考えると,内接球の中心IはAh上にあり,面ABCとの接点をTとすると点TはAM上にある。

$\text{DM}=6\sqrt{3}$, $\text{DH}=4\sqrt{3}$ より,
\begin{align*}
\text{MH}&=\text{DM}-\text{DH} \\[4pt]&=6\sqrt{3}-4\sqrt{3}=2\sqrt{3}
\end{align*}
内接球の半径を $r$ とする。$\sankaku{AMH}$∽$\sankaku{AIT}$ であるから\text{MH}&=\text{DM}-\text{DH} \\[4pt]&=6\sqrt{3}-4\sqrt{3}=2\sqrt{3}
\end{align*}
\begin{align*}
&\text{AM}:\text{MH}=\text{AI}:\text{IT} \\[4pt]&4\sqrt{3}:2\sqrt{3}=(6-r):r \\[4pt]&2r=6-r \\[4pt]&r=2
\end{align*}
このあとは球の体積を求めるだけなので省略する。&\text{AM}:\text{MH}=\text{AI}:\text{IT} \\[4pt]&4\sqrt{3}:2\sqrt{3}=(6-r):r \\[4pt]&2r=6-r \\[4pt]&r=2
\end{align*}

ヒロ
四面体の表面積と内接球の半径の関係は次のようになっていることを理解しよう。
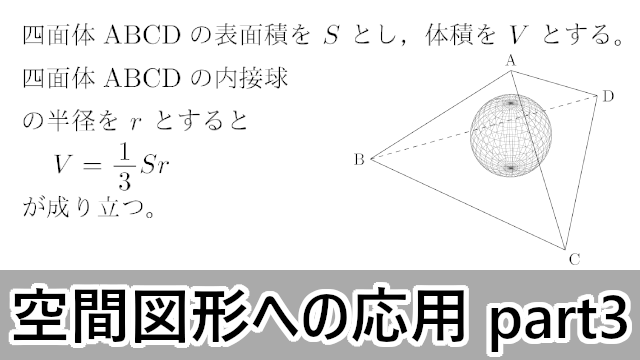
四面体と内接球四面体ABCDの表面積を $S$ とし,体積を $V$ とする。四面体ABCDの内接球の半径を $r$ とすると
\begin{align*}
V=\dfrac{1}{3}Sr
\end{align*}
が成り立つ。V=\dfrac{1}{3}Sr
\end{align*}

四面体と球の問題2

ヒロ
もう1問解いてみよう。
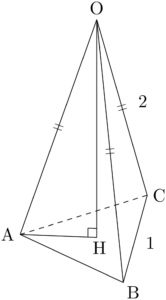
2018年 摂南大1辺の長さが1の正三角形ABCを底面とする四面体OABCが球 $S$ に内接している。$\text{OA}=\text{OB}=\text{OC}=2$ とする。頂点Oから三角形ABCに下ろした垂線の足をHとするとき,線分AHの長さは $\dfrac{\sqrt{\myhako}}{\myhako}$ である。また球 $S$ の半径は $\dfrac{\myhako\sqrt{\myhako}}{\myhako}$ である。
【考え方と解答】
$\text{OA}=\text{OB}=\text{OC}$ であるから,Hが $\sankaku{ABC}$ の外心であることが分かる。このことについては慣れてきただろう。
AHは $\sankaku{ABC}$ の外接円の半径であるから,正弦定理より
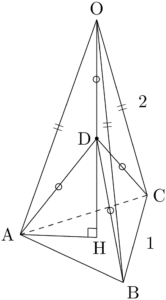
次に四面体OABCの外接球 $S$ の半径を求めよう。$S$ は4点O, A, B, Cを通るから,$S$ の中心をDとすると,
考えやすいように,$\sankaku{OAH}$ を取り出して考える。求める球の半径を $r$ とする。

三平方の定理より
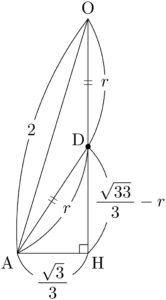
$\sankaku{ADH}$ において,三平方の定理より
$\text{OA}=\text{OB}=\text{OC}$ であるから,Hが $\sankaku{ABC}$ の外心であることが分かる。このことについては慣れてきただろう。

AHは $\sankaku{ABC}$ の外接円の半径であるから,正弦定理より
\begin{align*}
\text{AH}&=\dfrac{\text{BC}}{2\sin\kaku{BAC}} \\[4pt]&=\dfrac{1}{2\sin60\Deg}=\dfrac{1}{\sqrt{3}} \\[4pt]&=\dfrac{\sqrt{3}}{3}
\end{align*}
\text{AH}&=\dfrac{\text{BC}}{2\sin\kaku{BAC}} \\[4pt]&=\dfrac{1}{2\sin60\Deg}=\dfrac{1}{\sqrt{3}} \\[4pt]&=\dfrac{\sqrt{3}}{3}
\end{align*}
次に四面体OABCの外接球 $S$ の半径を求めよう。$S$ は4点O, A, B, Cを通るから,$S$ の中心をDとすると,
\begin{align*}
\text{DO}=\text{DA}=\text{DB}=\text{DC}
\end{align*}
を満たす。また,四面体OABCの対称性からDはOH上にあることが分かる。\text{DO}=\text{DA}=\text{DB}=\text{DC}
\end{align*}

考えやすいように,$\sankaku{OAH}$ を取り出して考える。求める球の半径を $r$ とする。

三平方の定理より
\begin{align*}
\text{OH}&=\sqrt{2^2-\left(\dfrac{\sqrt{3}}{3}\right)^2} \\[4pt]&=\dfrac{\sqrt{33}}{3}
\end{align*}
\text{OH}&=\sqrt{2^2-\left(\dfrac{\sqrt{3}}{3}\right)^2} \\[4pt]&=\dfrac{\sqrt{33}}{3}
\end{align*}

$\sankaku{ADH}$ において,三平方の定理より
\begin{align*}
&r^2=\left(\dfrac{\sqrt{3}}{3}\right)^2+\left(\dfrac{\sqrt{33}}{3}-r\right)^2 \\[4pt]&r^2=\dfrac{1}{3}+\dfrac{11}{3}-\dfrac{2\sqrt{33}}{3}r+r^2 \\[4pt]&\dfrac{2\sqrt{33}}{3}r=4 \\[4pt]&r=\dfrac{6}{\sqrt{33}}=\dfrac{2\sqrt{33}}{11}
\end{align*}
&r^2=\left(\dfrac{\sqrt{3}}{3}\right)^2+\left(\dfrac{\sqrt{33}}{3}-r\right)^2 \\[4pt]&r^2=\dfrac{1}{3}+\dfrac{11}{3}-\dfrac{2\sqrt{33}}{3}r+r^2 \\[4pt]&\dfrac{2\sqrt{33}}{3}r=4 \\[4pt]&r=\dfrac{6}{\sqrt{33}}=\dfrac{2\sqrt{33}}{11}
\end{align*}