ここでは円外の点から円に引いた接線について説明します。
「定点を通る直線の方程式」と「円と直線の位置関係」について分かっていることが前提となるため，記事を読んでいて良く分からなくなった場合は，次の記事を参考にすると解決するかもしれません。
【数学ⅡB】定点を通る直線の方程式と恒等式【京都薬科大】
ここでは定点を通る直線の方程式と恒等式について説明します。 前に扱った定点を通る直線では，直線の方程式が基本形で表されていて，傾きが変化するだけだったため，比較的簡単でした。 今回扱う直線の方程式は一般形で表されているため，少し難しくなりま...
methodology.site
2020.09.05
【数学ⅡB】円と直線の位置関係【北海学園大・久留米大】
ここでは円と直線の位置関係について説明します。 円と直線の位置関係は3つのパターンに分けられますが，与えられた円と直線の方程式からその位置関係を判断できるようになりましょう。 円と直線の位置関係 ヒロ 円と直線の位置関係は，次の3パターンに...
methodology.site
2020.09.12
Contents
円外の点から円に引いた接線
ヒロ
円外の点から円に引いた接線を求める方法を説明する。
円外の点Aから円 $C$ に引いた接線を求める上で，重要なのは接点の座標である。円周上にある接点Pの座標を簡単に求めることができれば良いが，それは中々難しい。
したがって，通過することが決まっている点Aを通る直線を先に考えて，それが円 $C$ に接する条件を考える。
例えば，点C$(a,~b)$ を中心とする半径 $r$ の円を $C$ とし，$C$ 上にない点A$(p,~q)$ から $C$ に引いた接線を考える。ただし，$a+r\neq p$ とする。$a+r=p$ のときは，直線 $x=p$ が接線の1つになる。
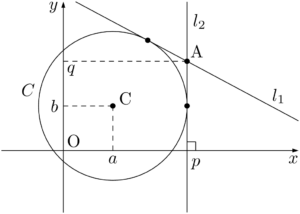
このような接線は簡単に求められるため，接線が $y$ 軸と平行でない場合を考えることにする。このとき，求める接線の方程式は
\begin{align*}
&y=m(x-p)+q \\[4pt]
&mx-y-mp+q=0
\end{align*}
と表せる。条件をみたす接線は下図のように $l_1$ と $l_2$ の2本あることが分かる。&y=m(x-p)+q \\[4pt]
&mx-y-mp+q=0
\end{align*}
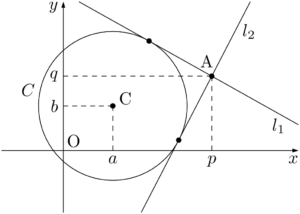
2接線 $l_1,~l_2$ と円 $C$ との接点をそれぞれP，Qとする。このとき，CP$\perp l_1$，CQ$\perp l_2$ であり，
\begin{align*}
\text{CP}=\text{CQ}=r
\end{align*}
である。\text{CP}=\text{CQ}=r
\end{align*}
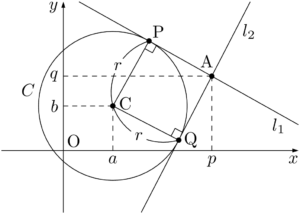
直線 $mx-y-mp+q=0$ と点C$(a,~b)$ との距離が $r$ であることから，$m$ を求める。点と直線の距離の公式を利用すると
\begin{align*}
&\dfrac{\abs{ma-b-mp+q}}{\sqrt{m^2+1}}=r
\end{align*}
となり，これを解くことで傾き $m$ が得られる。&\dfrac{\abs{ma-b-mp+q}}{\sqrt{m^2+1}}=r
\end{align*}
2つの解を $m_1,~m_2$ とすると，求める接線の方程式は
\begin{align*}
y=m_1(x-p)+q,~y=m_2(x-p)+q
\end{align*}
となる。$l_1$ と $l_2$ の区別は $m_1$ と $m_2$ の大小関係で判断できる。y=m_1(x-p)+q,~y=m_2(x-p)+q
\end{align*}