Contents
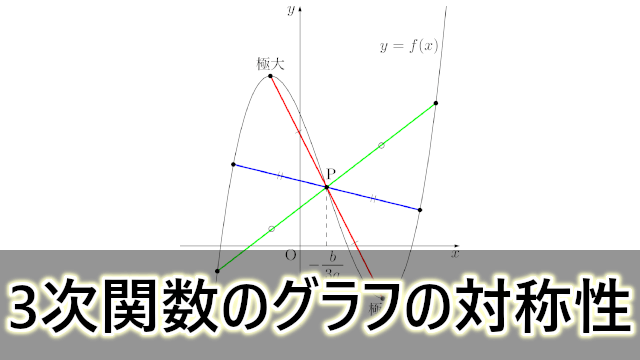
3次関数のグラフが点対称であることを証明する問題

ヒロ
それでは次の問題を解いてみよう。
問題$f(x)=ax^3+bx^2+cx+d~(a\neq0)$ とするとき,次の問いに答えよ。
(1) $f^{\prime\prime}(x)=0$ を解け。
(2) (1)の解を $\alpha$ とし,$\mathrm{P}(\alpha,~f(\alpha))$ とおく。点Pが原点にくるように $y=f(x)$ のグラフを平行移動したグラフの方程式を $y=g(x)$ とするとき,$g(x)$ を求めよ。
(3) $y=f(x)$ のグラフは点Pに関して点対称であることを示せ。
(1) $f^{\prime\prime}(x)=0$ を解け。
(2) (1)の解を $\alpha$ とし,$\mathrm{P}(\alpha,~f(\alpha))$ とおく。点Pが原点にくるように $y=f(x)$ のグラフを平行移動したグラフの方程式を $y=g(x)$ とするとき,$g(x)$ を求めよ。
(3) $y=f(x)$ のグラフは点Pに関して点対称であることを示せ。

ヒロ
$f^{\prime\prime}(x)$ は $f(x)$ を2回微分したもの。
【(1)の解答】
$f(x)=ax^3+bx^2+cx+d$ より
$f(x)=ax^3+bx^2+cx+d$ より
\begin{align*}
&f'(x)=3ax^2+2bx+c \\[4pt]
&f^{\prime\prime}(x)=6ax+2b
\end{align*}
となるから,$f^{\prime\prime}(x)=0$ とすると,$x=-\dfrac{b}{3a}$&f'(x)=3ax^2+2bx+c \\[4pt]
&f^{\prime\prime}(x)=6ax+2b
\end{align*}
グラフの平行移動$y=f(x)$ のグラフを $x$ 軸方向に $p$ ,$y$ 軸方向に $q$ だけ平行移動したグラフの方程式は
\begin{align*}
y=f(x-p)+q
\end{align*}
と表される。一般的には,$y-q=f(x-p)$ と書かれているけど,それを書いてから $-q$ を移項するのは面倒なので右辺に書いている。そもそも $x=p$ のときに $y=q$ になることを考えると,右辺に直接 $q$ を書く方が自然だと考えている。また,この書き方をすることで1行短くなるのでオススメ。y=f(x-p)+q
\end{align*}
【(2)の解答】
点 $\mathrm{P}(\alpha,~f(\alpha))$ が原点にくるようにするには,$x$ 軸方向に $-\alpha$,$y$ 軸方向に $-f(\alpha)$ だけ平行移動すればよい。
(1)より,$\alpha=-\dfrac{b}{3a}$ だから,
点 $\mathrm{P}(\alpha,~f(\alpha))$ が原点にくるようにするには,$x$ 軸方向に $-\alpha$,$y$ 軸方向に $-f(\alpha)$ だけ平行移動すればよい。
(1)より,$\alpha=-\dfrac{b}{3a}$ だから,
\begin{align*}
g(x)&=f\left(x-\dfrac{b}{3a}\right)-f\left(-\dfrac{b}{3a}\right) \\[4pt]
&=a\left(x-\dfrac{b}{3a}\right)^3+b\left(x-\dfrac{b}{3a}\right)^2
+c\left(x-\dfrac{b}{3a}\right)+d-f\left(-\dfrac{b}{3a}\right) \\[4pt]
&=a\left(x^3-3x^2\cdot\dfrac{b}{3a}+3x\cdot\dfrac{b^2}{9a^2}\right)
+bx^2-\dfrac{2b^2}{3a}x+cx \\[4pt]
&=ax^3-\left(\dfrac{b^2}{3a}-c\right)x
\end{align*}
g(x)&=f\left(x-\dfrac{b}{3a}\right)-f\left(-\dfrac{b}{3a}\right) \\[4pt]
&=a\left(x-\dfrac{b}{3a}\right)^3+b\left(x-\dfrac{b}{3a}\right)^2
+c\left(x-\dfrac{b}{3a}\right)+d-f\left(-\dfrac{b}{3a}\right) \\[4pt]
&=a\left(x^3-3x^2\cdot\dfrac{b}{3a}+3x\cdot\dfrac{b^2}{9a^2}\right)
+bx^2-\dfrac{2b^2}{3a}x+cx \\[4pt]
&=ax^3-\left(\dfrac{b^2}{3a}-c\right)x
\end{align*}

ヒロ
関数 $g(x)$ は1次と3次の項のみだから,奇関数と分かるね。
【(3)の解答】
(2)において,
よって,$y=f(x)$ のグラフは点Pに関して点対称である。
(2)において,
\begin{align*}
g(-x)&=a(-x)^3-\left(\dfrac{b^2}{3a}-c\right)(-x) \\[4pt]
&=-ax^3+\left(\dfrac{b^2}{3a}-c\right)x \\[4pt]
&=-g(x)
\end{align*}
となるから,$y=g(x)$ のグラフは原点に関して点対称である。g(-x)&=a(-x)^3-\left(\dfrac{b^2}{3a}-c\right)(-x) \\[4pt]
&=-ax^3+\left(\dfrac{b^2}{3a}-c\right)x \\[4pt]
&=-g(x)
\end{align*}
よって,$y=f(x)$ のグラフは点Pに関して点対称である。