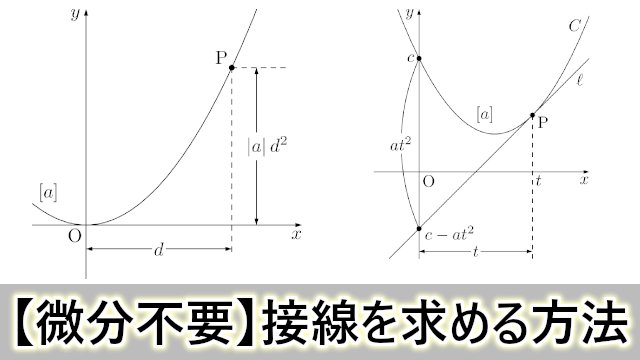
放物線の接線を求める問題において,接点に着目すると次の2種類に分けることができます。
- 接点が放物線上にある
- 接点が放物線上にない
接点が放物線上にある場合は,微分係数を求めることで接線の方程式を簡単に求めることができます。しかし,接点が放物線上にない問題では,少し面倒です。一般的に,接点の $x$ 座標を $t$ とおくことが基本的な解法です。あとは微分を利用して微分係数を求めることで接線の方程式を求めることができます。
私大入試によく見られるような答えだけを書けばよい試験では,いかに速く正確に求められるかが重要になります。
この記事では,微分を用いないで,放物線上にない点から放物線に引いた接線の方程式を簡単に求める方法を説明します。
プリントを次のリンクからダウンロードできます。
Contents
2次関数は2乗に比例する性質をもつ関数である

2次関数の最も基本となる形は $y=ax^2$ で,中3のときに $x$ の2乗に比例する関数と習ったね。今日はその意味をもう少し掘り下げて理解を深めよう。

関数 $y=ax^2$ において,$x$ の $x=0$ からの増加量が $d$ のとき,比例定数が $a$ だから $y$ の増加量は $ad^2$ になる。

これをグラフで考えると,$y=ax^2$ 上の $x$ 座標が $d$ の点をPとすると,Pの $y$ 座標が $\abs{a}d^2$ ということだね。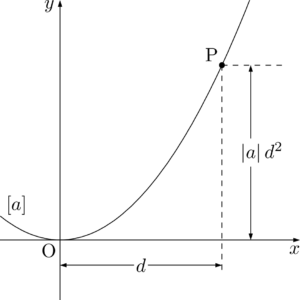

ここで,$C:y=\dfrac{1}{2}(x-2)^2+1$ 上の点 $\mathrm{P}\left(3,~\dfrac{3}{2}\right)$ における接線 $\ell$ を考えてみよう。
y’=x-2
\end{align*}
y=x-\dfrac{3}{2}
\end{align*}
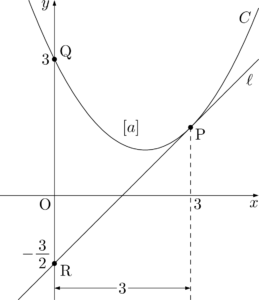
ここで,QRの長さを求めると
\mathrm{QR}=3-\left(-\dfrac{3}{2}\right)=\dfrac{9}{2}
\end{align*}
(x^2\, の係数)\times(接点と \,y\, 軸との距離)=\dfrac{1}{2}\times3^2
\end{align*}

この意味をしっかり理解しよう。
f(x)-g(x)&=\dfrac{1}{2}(x-2)^2+1-\left(x-\dfrac{3}{2}\right) \\[4pt]
&=\dfrac{1}{2}(x-3)^2
\end{align*}

展開して計算しても,もちろん同じ結果になるけど,接するという意味を考えてサクッと変形できるようにしよう。

ここからが重要。$y=f(x)-g(x)$ のグラフを描くと次のようになる。
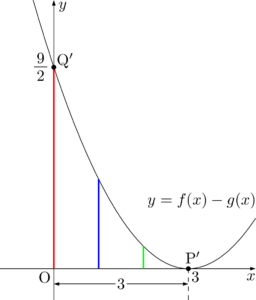
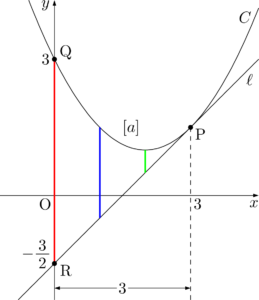
3点P, Q, RはそれぞれP$’$, Q$’$, Oに移る。$y=f(x)-g(x)$ のグラフは $f(x)$ と $g(x)$ の差を表しているから,2つの図において,それぞれ $x$ 座標が等しい赤・青・緑の線分の長さは,それぞれ等しくなる。

これを接線の切片を求めるのに利用すると次のようになる。
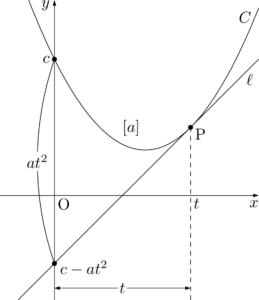
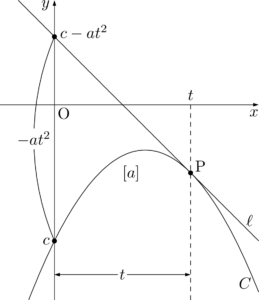
(接線 \ell の切片)&=(放物線の切片)-(x^2 の係数)\times(接点と y 軸の距離) \\[4pt]
&=c-at^2
\end{align*}

この知識を応用すると,放物線上にない点から放物線に引いた接線を簡単に求めることができる。
微分を用いて放物線上にない点から放物線に引いた接線の式を求める方法

次の問題を解いてみよう。

まずは,通常の手順で接線の方程式を求めよう。
- $f'(x)$ を求める。
- 接点の座標を $(t,~f(t))$ として,接線の方程式を求める。\begin{align*}となる。
y=f'(t)(x-t)+f(t)~\cdots\cdots ①
\end{align*} - ①が点 $(a,~b)$ を通る条件から $t$ を求める。すなわち\begin{align*}を解く。
b=f'(t)(a-t)+f(t)
\end{align*} - 求めた $t$ の値を①に代入して,接線の方程式を求める。
※ただし,曲線の方程式を $y=f(x)$,通る点の座標を $(a,~b)$ とする。
f'(x)=-2x+4
\end{align*}
y=(-2t+4)x+t^2-3~\cdots\cdots ①
\end{align*}
&4=3(-2t+4)+t^2-3 \\[4pt]
&t^2-6t+5=0 \\[4pt]
&(t-1)(t-5)=0 \\[4pt]
&t=1,~5
\end{align*}
y=2x-2,~y=-6x+22
\end{align*}
微分を用いずに放物線上にない点から放物線に引いた接線の式を求める方法

それでは放物線の性質を利用することで,微分を用いずに,接線の方程式を簡単に求める方法を説明していく。

まず,放物線の性質を利用して,接点の $x$ 座標を求めよう。
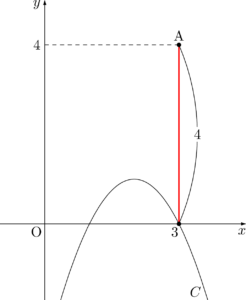
点Aから放物線 $C$ に接線APとAQを引いた状態を考える。点Aを通り,$y$ 軸に平行な直線と放物線 $C$ との交点をRとすると,2つの接点P, Qと直線ARとの距離は等しくなり,その距離を $d~(>0)$ とすると,$\mathrm{AR}=\abs{a}d^2$ が成り立つ。
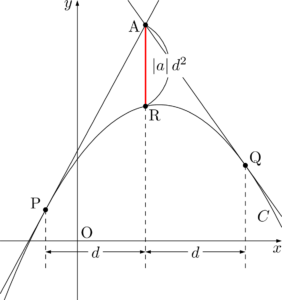
点 $(3,~4)$ から,放物線 $y=-x^2+4x-3$ に引いた接線の方程式を求めよ。
y=-9+12-3=0
\end{align*}
&d^2=4
\end{align*}
よって,接点の $x$ 座標は
&3\pm d=3\pm2=1,~5
\end{align*}
y=-1+4-3=0
\end{align*}
y=-25+20-3=-8
\end{align*}
\mathrm{P}(1,~0),~\mathrm{Q}(5,~-8)
\end{align*}
&y=2(x-1) \\[4pt]
&y=2x-2
\end{align*}
&y=-6(x-3)+4 \\[4pt]
&y=-6x+22
\end{align*}
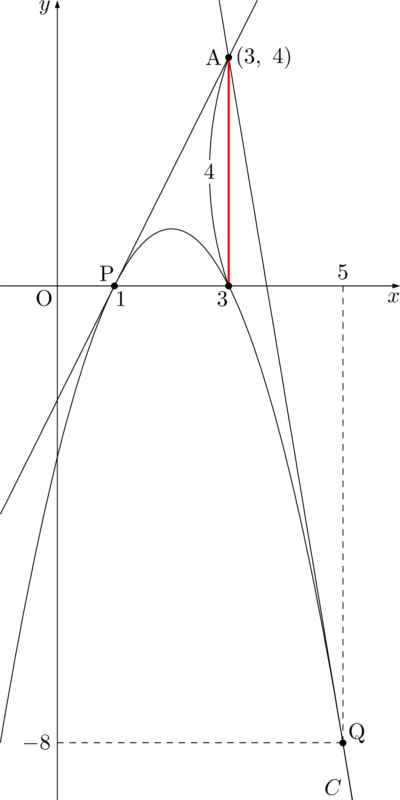

このように,微分を使わずに接線を求めることも可能である。しかし,完全に理解するためには,グラフの位置関係と連立方程式の解の関係など,様々な知識が必要となる。
まとめ

関数 $y=ax^2$ は $x^2$ に比例する関数であり,放物線 $y=ax^2+bx+c$ は放物線 $y=ax^2$ を平行移動したものであることは,ほとんどの高校生にとって常識である。しかし,「放物線と接線の差も接点から $x$ 軸と平行な方向の移動量の2乗に比例する」ということを常識であると認識して,さらに有効活用している人は少ない。

2次関数はすべて,2乗に比例する関数である。この性質をうまく利用することで,放物線上にない点から放物線に引いた接線の方程式を,微分を使うこともなく,簡単に求めることができる。

また,放物線はすべて相似であることも知られている。興味がある人は次の記事が参考になるだろう。

この記事で説明している共通接線の求め方もいわゆる「裏技」に分類されるかもしれない。

このような裏技は好き嫌いが別れるだろうが,マーク式試験や答えだけを記入すればよい試験では,裏技公式というものを知っていると有利になることは間違いない。