Contents
極値の和に関する入試問題

ヒロ
次の問題を解いてみよう。
入試問題$f(x)=x^3+ax^2+2x-2a$ が2つの異なる極値をもち,しかも極大値と極小値の和が0となるように定数 $a$ の値を定めよ。
一般的な解答

ヒロ
まずは,一般的な解答。
$f(x)$ が異なる極値をもつとき,$f'(x)=0$ が異なる2つの実数解をもつから,
\begin{align*}
f'(x)=3x^2+2ax+2=0
\end{align*}
が異なる2つの実数解をもつ。f'(x)=3x^2+2ax+2=0
\end{align*}
\begin{align*}
&a^2-6>0 \\[4pt]
&a<-\sqrt6,~\sqrt6<a~\cdots\cdots①
\end{align*}
$f'(x)=0$ の2解を $\alpha,~\beta$ とすると,&a^2-6>0 \\[4pt]
&a<-\sqrt6,~\sqrt6<a~\cdots\cdots①
\end{align*}
\begin{align*}
\alpha+\beta=-\dfrac{2}{3}a,~\alpha\beta=\dfrac{2}{3}~\cdots\cdots②
\end{align*}
極大値と極小値の和が0であるから,\alpha+\beta=-\dfrac{2}{3}a,~\alpha\beta=\dfrac{2}{3}~\cdots\cdots②
\end{align*}
\begin{align*}
&f(\alpha)+f(\beta)=0 \\[4pt]
&(\alpha^3+\beta^3)+a(\alpha^2+\beta^2)+2(\alpha+\beta)-4a=0~\cdots\cdots③
\end{align*}
②より,&f(\alpha)+f(\beta)=0 \\[4pt]
&(\alpha^3+\beta^3)+a(\alpha^2+\beta^2)+2(\alpha+\beta)-4a=0~\cdots\cdots③
\end{align*}
\begin{align*}
\alpha^2+\beta^2&=(\alpha+\beta)^2-2\alpha\beta \\[4pt]
&=\left(-\dfrac{2}{3}a\right)^2-2\Cdota\dfrac{2}{3} \\[4pt]
&=\dfrac{4}{9}a^2-\dfrac{4}{3} \\[4pt]
\alpha^3+\beta^3&=(\alpha+\beta)^3-3\alpha\beta(\alpha+\beta) \\[4pt]
&=\left(-\dfrac{2}{3}a\right)^3-3\Cdota\dfrac{2}{3}\Cdota\left(-\dfrac{2}{3}a\right) \\[4pt]
&=-\dfrac{8}{27}a^3+\dfrac{4}{3}a
\end{align*}
であるから,③より,\alpha^2+\beta^2&=(\alpha+\beta)^2-2\alpha\beta \\[4pt]
&=\left(-\dfrac{2}{3}a\right)^2-2\Cdota\dfrac{2}{3} \\[4pt]
&=\dfrac{4}{9}a^2-\dfrac{4}{3} \\[4pt]
\alpha^3+\beta^3&=(\alpha+\beta)^3-3\alpha\beta(\alpha+\beta) \\[4pt]
&=\left(-\dfrac{2}{3}a\right)^3-3\Cdota\dfrac{2}{3}\Cdota\left(-\dfrac{2}{3}a\right) \\[4pt]
&=-\dfrac{8}{27}a^3+\dfrac{4}{3}a
\end{align*}
\begin{align*}
&\dfrac{4}{27}a^3-\dfrac{16}{3}a=0 \\[4pt]
&a(a^2-36)=0 \\[4pt]
&a=0,~\pm6
\end{align*}
$①$より,$a=\pm6$&\dfrac{4}{27}a^3-\dfrac{16}{3}a=0 \\[4pt]
&a(a^2-36)=0 \\[4pt]
&a=0,~\pm6
\end{align*}
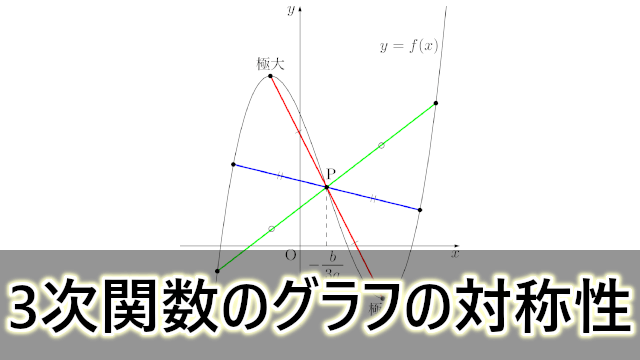
3次関数のグラフの対称性を利用した考え方

ヒロ
次は3次関数のグラフが変曲点に関して対称であることを利用する場合。

ヒロ
変曲点の $x$ 座標は $-\dfrac{a}{3}$ となるから,条件より $f\left(-\dfrac{a}{3}\right)=0$ を満たす $a$ を求めれば良いと分かる。答えだけで良いなら,2つの異なる極値をもつ条件を求めた後,$f\left(-\dfrac{a}{3}\right)=0$ を解けば良い。

ヒロ
記述式なら次のように書いておけば問題ない。
①を求めるところまでは同じ。
点 $(p,~f(p))$ に関して,点 $(x,~y)$ の対称な点を $(X,~Y)$ とすると,
\begin{align*}
X=-x+2p,~Y=-y+2f(p)
\end{align*}
が成り立つ。$y=f(x)$ のグラフが点 $(p,~f(p))$ に関して点対称であるとき,$Y=f(X)$ が成り立つから,X=-x+2p,~Y=-y+2f(p)
\end{align*}
\begin{align*}
&-y+2f(p)=f(2p-x) \\[4pt]
&y=2f(p)-f(2p-x)
\end{align*}
が成り立つ。ここで,&-y+2f(p)=f(2p-x) \\[4pt]
&y=2f(p)-f(2p-x)
\end{align*}
\begin{align*}
&2f\left(-\dfrac{1}{3}a\right)-f\left(-\dfrac{2}{3}a-x\right) \\[4pt]
&=2\left\{\left(-\dfrac{1}{3}a\right)^3+a\left(-\dfrac{1}{3}a\right)^2+2\left(-\dfrac{1}{3}a\right)-2a\right\} \\[4pt]
&\hspace{10pt}-\left\{\left(-\dfrac{2}{3}a-x\right)^3+a\left(-\dfrac{2}{3}a-x\right)^2+2\left(-\dfrac{2}{3}a-x\right)-2a\right\} \\[4pt]
&=x^3+ax^2+2x-2a \\[4pt]
&=f(x)
\end{align*}
よって,$y=f(x)$ のグラフは点 $\left(-\dfrac{1}{3}a,~f\left(-\dfrac{1}{3}a\right)\right)$ に関して点対称である。&2f\left(-\dfrac{1}{3}a\right)-f\left(-\dfrac{2}{3}a-x\right) \\[4pt]
&=2\left\{\left(-\dfrac{1}{3}a\right)^3+a\left(-\dfrac{1}{3}a\right)^2+2\left(-\dfrac{1}{3}a\right)-2a\right\} \\[4pt]
&\hspace{10pt}-\left\{\left(-\dfrac{2}{3}a-x\right)^3+a\left(-\dfrac{2}{3}a-x\right)^2+2\left(-\dfrac{2}{3}a-x\right)-2a\right\} \\[4pt]
&=x^3+ax^2+2x-2a \\[4pt]
&=f(x)
\end{align*}

ヒロ
$p=-\dfrac{a}{3}$ のときに $f(x)=2f(p)-f(2p-x)$ が成り立つことを知っているので,あたかも計算したように書いておけば減点されることはない。あとは$f\left(-\dfrac{a}{3}\right)=0$ を解いて終わりだね。
極大値と極小値の和が0になるとき,
\begin{align*}
f\left(-\dfrac{1}{3}a\right)=0
\end{align*}
となるからf\left(-\dfrac{1}{3}a\right)=0
\end{align*}
\begin{align*}
&-\dfrac{a^3}{27}+\dfrac{a^3}{9}-\dfrac{2}{3}a-2a=0 \\[4pt]
&\dfrac{2}{27}a^3-\dfrac{8}{3}a=0 \\[4pt]
&\dfrac{2}{27}a(a^2-36)=0 \\[4pt]
&a=0,~\pm6
\end{align*}
$①$より,$a=\pm6$&-\dfrac{a^3}{27}+\dfrac{a^3}{9}-\dfrac{2}{3}a-2a=0 \\[4pt]
&\dfrac{2}{27}a^3-\dfrac{8}{3}a=0 \\[4pt]
&\dfrac{2}{27}a(a^2-36)=0 \\[4pt]
&a=0,~\pm6
\end{align*}
3次関数の対称性についてのまとめ

ヒロ
すべての3次関数のグラフは変曲点に関して対称である。

ヒロ
3次関数のグラフの対称性を利用して,今までよりキレイに3次関数のグラフ描こう。また,極値に関する問題を解くときにも活かせるようにしよう。