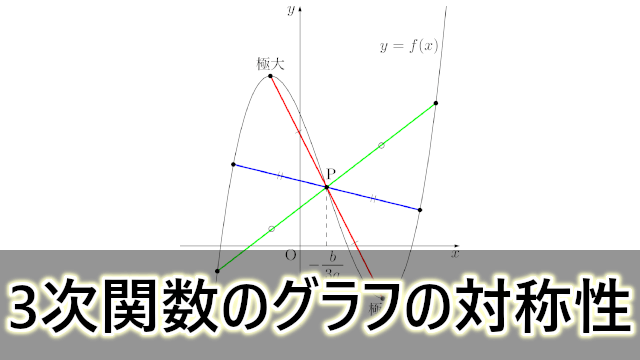
すべての3次関数のグラフは変曲点に関して点対称であることが知られています。変曲点については,数学IIIを学習している人にとっては常識かもしれませんが,そうでない人にとっては知らないことかもしれません。3次関数のグラフの対称性を知ることで,グラフをキレイに描くこともできるようになります。
Contents
点Pに関して点Aと対称な点B【線対称と点対称】

ヒロ
まずは簡単な問題から1つずつ理解していこう。
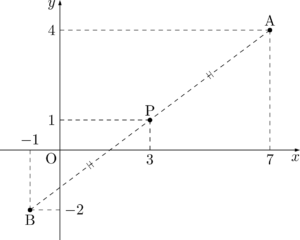
例題12点A, Pの座標を $\mathrm{A}(7,~4),~\mathrm{P}(3,~1)$ とする。点Pに関して点Aと対称な点Bの座標を求めよ。

ヒロ
対称と聞くと「線対称」や「点対称」を思い浮かべるだろう。
線対称1つの直線を折り目にして折ったとき,折り目の両側がぴったり重なる図形は,線対称または直線について対称であるという。また,その折り目にした直線を対称の軸という。
点対称ある点のまわりに $180\Deg$ まわすと,元の形にぴったり重なる図形は,点対称または点について対称であるという。また,その点を対称の中心という。

ヒロ
例題1では,「点Pに関して対称」とあるから,点対称に関する話をしていて,点Pが対称の中心であることを読み取ろう。

ヒロ
つまり「点Pのまわりに点Aを $180\Deg$ まわすと点Bに重なるよ」と書かれている。これは2点A, Bの中点が点Pであると言い換えることができる。
点Bの座標を $(x,~y)$ とすると,2点A, Bの中点が点Pであるから
\begin{align*}
&\dfrac{x+7}{2}=3\,,~~\dfrac{y+4}{2}=1 \\[4pt]
&x=1,~y=-2
\end{align*}
&\dfrac{x+7}{2}=3\,,~~\dfrac{y+4}{2}=1 \\[4pt]
&x=1,~y=-2
\end{align*}


ヒロ
さらに別の言い方をすると,点Bは線分APを $2:1$ に外分する点ということもできる。
外分点「線分ABを $m:n$ の比に外分する」を「線分ABを $m:(-n)$ の比に内分する」と言い換えることで内分点の公式を利用することができる。ちなみに $m$ と $n$ のどちらの符号を変えても構わない。教科書では $n$ を $-n$ にするように書かれているが,$m$ と $n$ を比べて小さい方を負に変えれば良い。つまり分母が正になるように符号を変えた方が良く,その方が符号による間違いが少なくなり正しく計算できる確率が上がる。
点Bの座標を $(x,~y)$ とすると,点Bは線分APを $2:1$ に外分する点であるから
\begin{align*}
&x=\dfrac{2\Cdot3+(-1)\Cdot7}{2-1}=-1 \\[4pt]
&y=\dfrac{2\Cdot1+(-1)\Cdot4}{2-1}=-2
\end{align*}
&x=\dfrac{2\Cdot3+(-1)\Cdot7}{2-1}=-1 \\[4pt]
&y=\dfrac{2\Cdot1+(-1)\Cdot4}{2-1}=-2
\end{align*}

ヒロ
上の2つの考え方のうち,どちらの考え方であっても点Bの座標を $\mathrm{B}(-1,~-2)$ と求めることができる。