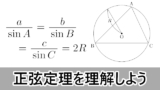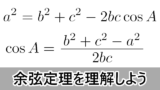ここでは三角形の形状決定問題について説明します。
三角形の形状を大きく分類すると
- 鋭角三角形
- 直角三角形
- 鈍角三角形
の3つに分けることができます。
これについては次の記事で説明しているので，参考にして下さい。
今回はもう少し詳しい形状を考えます。
つまり，直角三角形なら「どの角が直角であるか」や，二等辺三角形なら「どの2辺の長さが等しいか」などについても触れて答えるようにします。
正弦定理と余弦定理を使いこなせることが前提となっているため，知識があやふやな人は復習しておきましょう。
【数学IA】正弦定理を理解しよう
ここでは正弦定理について説明します。 正弦とはサインのことで，定理の名前の通り，サインに関する定理が「正弦定理」です。 直角三角形だけでなく，一般的な三角形に成り立つ定理なので，様々な問題で利用することになります。 定理の内容を理解して使え...
methodology.site
2020.06.05
【数学IA】余弦定理を理解しよう
ここでは余弦定理について説明します。 余弦とはコサインのことで，定理の名前の通り，コサインに関する定理が「余弦定理」です。 正弦定理と同様に，直角三角形だけでなく一般的な三角形に成り立つ定理なので，様々な問題で利用することになります。 定理...
methodology.site
2020.06.06
【数学IA】三角形に関する等式の証明
ここでは三角形に関する等式の証明問題について説明します。 三角比の相互関係を利用した等式の証明問題についての解説記事は，次の記事を参考にして下さい。 三角形に関する等式の証明問題 問題$\sankaku{ABC}$ において，次の等式が成り...
methodology.site
2020.06.12
三角形の形状決定問題の基本的な考え方
ヒロ
まずは三角形の形状決定問題の基本的な考え方を身に付けよう。
三角形の形状決定問題正弦定理や余弦定理を用いて，辺だけの式に変形するのが基本である。場合によっては角だけの式に変形するのも有効である。
ヒロ
辺だけの式に変形したあとは，因数分解できるかどうかで解けるかどうかが決まる。
【数学Ⅰ】定期テストに出題される因数分解の問題
大学入試で「○○を因数分解せよ」という問題が出題されたときには，必ず解けることが合格への必須の条件だと言えるくらい因数分解は重要です。 高校1年生で学習する因数分解は，中学校で学習する因数分解より難しいです。 その複雑さから挫折すると，その...
methodology.site
2020.02.26
【数学Ⅰ】定期テストに出題される因数分解の問題 part2
数学Ⅰで学習する因数分解は，高校数学の中でも特に重要な単元です。 うまく因数分解できないと解ける問題も解けなくなってしまいます。 因数分解の問題は，単独では大学入試にそれほど出題されるわけではないですが，しっかりできるようにしていきましょう...
methodology.site
2020.02.27
ヒロ
実際に出題された入試問題を解いてみよう。
2007年 長崎県立大
問題$\sankaku{ABC}$ において，等式
\begin{align*}
\sin A=2\cos B\sin C
\end{align*}
が成り立つとき，この三角形はどのような形をしているか求めなさい。\sin A=2\cos B\sin C
\end{align*}
プリントを次のリンクからダウンロードできます。
【考え方と解答】
$\sankaku{ABC}$ の外接円の半径を $R$ とすると，正弦定理より
よって，$\sankaku{ABC}$ は $\text{AB}=\text{AC}$ である二等辺三角形である。
$\sankaku{ABC}$ の外接円の半径を $R$ とすると，正弦定理より
\begin{align*}
\sin A=\dfrac{a}{2R},~\sin B=\dfrac{b}{2R},~\sin C=\dfrac{c}{2R}
\end{align*}
であり，余弦定理より\sin A=\dfrac{a}{2R},~\sin B=\dfrac{b}{2R},~\sin C=\dfrac{c}{2R}
\end{align*}
\begin{align*}
&\cos B=\dfrac{c^2+a^2-b^2}{2ca}
\end{align*}
であるから，与えられた等式より&\cos B=\dfrac{c^2+a^2-b^2}{2ca}
\end{align*}
\begin{align*}
&\dfrac{a}{2R}=2\Cdota\dfrac{c^2+a^2-b^2}{2ca}\Cdota\dfrac{c}{2R} \\[4pt]
&a^2=c^2+a^2-b^2 \\[4pt]
&(b+c)(b-c)=0
\end{align*}
$b+c\neq0$ より，$b=c$&\dfrac{a}{2R}=2\Cdota\dfrac{c^2+a^2-b^2}{2ca}\Cdota\dfrac{c}{2R} \\[4pt]
&a^2=c^2+a^2-b^2 \\[4pt]
&(b+c)(b-c)=0
\end{align*}
よって，$\sankaku{ABC}$ は $\text{AB}=\text{AC}$ である二等辺三角形である。
2005年 宮城教育大
問題$\sankaku{ABC}$ の3つの角 $\kaku{A},~\kaku{B},~\kaku{C}$ の大きさをそれぞれ $A,~B,~C$ とし，それらの角の対辺の長さをそれぞれ $a,~b,~c$ で表す。次の問に理由とともに答えよ。
(1) $\sankaku{ABC}$ が $\sin A+\cos A=1$ をみたすとき，$\sankaku{ABC}$ はどのような三角形であるか。
(2) $\sankaku{ABC}$ が $a\sin A=b\sin B$ をみたすとき，$\sankaku{ABC}$ はどのような三角形であるか。
(3) $\sankaku{ABC}$ が $2\cos B\cdot\sin C=\sin A$ をみたすとき，$\sankaku{ABC}$ はどのような三角形であるか。
(1) $\sankaku{ABC}$ が $\sin A+\cos A=1$ をみたすとき，$\sankaku{ABC}$ はどのような三角形であるか。
(2) $\sankaku{ABC}$ が $a\sin A=b\sin B$ をみたすとき，$\sankaku{ABC}$ はどのような三角形であるか。
(3) $\sankaku{ABC}$ が $2\cos B\cdot\sin C=\sin A$ をみたすとき，$\sankaku{ABC}$ はどのような三角形であるか。
【(1)の考え方と解答】
$\sin A$ と $\cos A$ がどちらも1次だから，どちらか一方に統一することはできない（無理やりならできるけど意味がない）。あとは利用できるのは $\sin^2A+\cos^2A=1$ であるから，両辺を2乗してみよう。
$\sin A+\cos A=1$ の両辺を2乗すると
よって，$A=90\Deg$ となるから，$\sankaku{ABC}$ は $A=90\Deg$ の直角三角形である。
$\sin A$ と $\cos A$ がどちらも1次だから，どちらか一方に統一することはできない（無理やりならできるけど意味がない）。あとは利用できるのは $\sin^2A+\cos^2A=1$ であるから，両辺を2乗してみよう。
$\sin A+\cos A=1$ の両辺を2乗すると
\begin{align*}
&(\sin A+\cos A)^2=1 \\[4pt]
&\cos^2A+2\sin A\cos A+\cos^2A=1 \\[4pt]
&1+2\sin A\cos A=1 \\[4pt]
&\sin A\cos A=0
\end{align*}
$A$ は三角形の内角の1つであるから，$\sin A\neq0$ となるから $\cos A=0$ である。&(\sin A+\cos A)^2=1 \\[4pt]
&\cos^2A+2\sin A\cos A+\cos^2A=1 \\[4pt]
&1+2\sin A\cos A=1 \\[4pt]
&\sin A\cos A=0
\end{align*}
よって，$A=90\Deg$ となるから，$\sankaku{ABC}$ は $A=90\Deg$ の直角三角形である。
(2) $\sankaku{ABC}$ が $a\sin A=b\sin B$ をみたすとき，$\sankaku{ABC}$ はどのような三角形であるか。
【(2)の考え方と解答】
$\sankaku{ABC}$ の外接円の半径を $R$ とすると，正弦定理より
よって，$\sankaku{ABC}$ は $\text{BC}=\text{AC}$ の二等辺三角形である。
$\sankaku{ABC}$ の外接円の半径を $R$ とすると，正弦定理より
\begin{align*}
\sin A=\dfrac{a}{2R},~\sin B=\dfrac{b}{2R}
\end{align*}
であるから，与えられた等式より\sin A=\dfrac{a}{2R},~\sin B=\dfrac{b}{2R}
\end{align*}
\begin{align*}
&a\Cdota\dfrac{a}{2R}=b\Cdota\dfrac{b}{2R} \\[4pt]
&a^2=b^2
\end{align*}
$a,~b$ はともに正であるから，$a=b$&a\Cdota\dfrac{a}{2R}=b\Cdota\dfrac{b}{2R} \\[4pt]
&a^2=b^2
\end{align*}
よって，$\sankaku{ABC}$ は $\text{BC}=\text{AC}$ の二等辺三角形である。
(3) $\sankaku{ABC}$ が $2\cos B\cdot\sin C=\sin A$ をみたすとき，$\sankaku{ABC}$ はどのような三角形であるか。
【(3)の考え方と解答】
$\sankaku{ABC}$ の外接円の半径を $R$ とすると，与えられた等式より
よって，$\sankaku{ABC}$ は $\text{AB}=\text{AC}$ の二等辺三角形である。
$\sankaku{ABC}$ の外接円の半径を $R$ とすると，与えられた等式より
\begin{align*}
&2\Cdota\dfrac{c^2+a^2-b^2}{2ca}\Cdota\dfrac{c}{2R}=\dfrac{a}{2R} \\[4pt]
&c^2+a^2-b^2=a^2 \\[4pt]
&b^2=c^2
\end{align*}
$b,~c$ はともに正であるから $b=c$&2\Cdota\dfrac{c^2+a^2-b^2}{2ca}\Cdota\dfrac{c}{2R}=\dfrac{a}{2R} \\[4pt]
&c^2+a^2-b^2=a^2 \\[4pt]
&b^2=c^2
\end{align*}
よって，$\sankaku{ABC}$ は $\text{AB}=\text{AC}$ の二等辺三角形である。
2003年 横浜国立大
問題$\sankaku{ABC}$ において $a=\text{BC}$, $b=\text{CA}$, $c=\text{AB}$ とする。
\begin{align*}
a^2\cos A\sin B=b^2\cos B\sin A
\end{align*}
が成り立つとき，$\sankaku{ABC}$ はどのような形か。a^2\cos A\sin B=b^2\cos B\sin A
\end{align*}
【考え方と解答】
$\sankaku{ABC}$ の外接円の半径を $R$ とする。与えられた等式において，正弦定理と余弦定理を用いると
よって，$\sankaku{ABC}$ は $a=b$ の二等辺三角形 または $\kaku{C}=90\Deg$ の直角三角形である。
$\sankaku{ABC}$ の外接円の半径を $R$ とする。与えられた等式において，正弦定理と余弦定理を用いると
\begin{align*}
&a^2\Cdota\dfrac{b^2+c^2-a^2}{2bc}\Cdota\dfrac{b}{2R}=b^2\Cdota\dfrac{c^2+a^2-b^2}{2ca}\Cdota\dfrac{a}{2R} \\[4pt]
&a^2(b^2+c^2-a^2)=b^2(c^2+a^2-b^2) \\[4pt]
&a^2c^2-a^4=b^2c^2-b^4 \\[4pt]
&a^4-b^4-c^2(a^2-b^2)=0 \\[4pt]
&(a^2-b^2)(a^2+b^2-c^2)=0 \\[4pt]
&(a+b)(a-b)(a^2+b^2-c^2)=0
\end{align*}
$a+b\neq0$ であるから，$a=b$ または $a^2+b^2=c^2$&a^2\Cdota\dfrac{b^2+c^2-a^2}{2bc}\Cdota\dfrac{b}{2R}=b^2\Cdota\dfrac{c^2+a^2-b^2}{2ca}\Cdota\dfrac{a}{2R} \\[4pt]
&a^2(b^2+c^2-a^2)=b^2(c^2+a^2-b^2) \\[4pt]
&a^2c^2-a^4=b^2c^2-b^4 \\[4pt]
&a^4-b^4-c^2(a^2-b^2)=0 \\[4pt]
&(a^2-b^2)(a^2+b^2-c^2)=0 \\[4pt]
&(a+b)(a-b)(a^2+b^2-c^2)=0
\end{align*}
よって，$\sankaku{ABC}$ は $a=b$ の二等辺三角形 または $\kaku{C}=90\Deg$ の直角三角形である。