3次関数のグラフには様々な特徴があります。この記事では3次関数のグラフの等間隔性について説明します。他のサイトでは「3次関数の4等分の法則」や「縦4個×横2個の合同な四角形に埋め込まれる」「5点定理」など,様々な表現方法があるみたいですが,当サイトでは「等間隔性」と表現することにします。
3次関数の等間隔性を知ることで,3次関数のグラフと接線の関係など様々な問題に対して,今までとは異なる考え方ができるようになるかもしれません。
Contents
3次関数のグラフの等間隔性

まず,3次関数のグラフにどのような特徴があるかを知ろう。
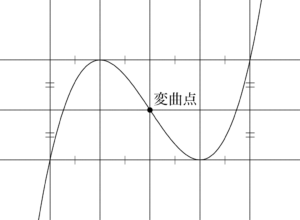
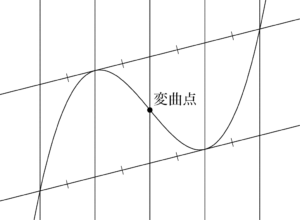
3次関数のグラフと接線の関係

3次関数のグラフの等間隔性を理解するために,まずは,次の例題を解いて3次関数のグラフと接線の関係について知ろう。
(1) $C:y=f(x)$ 上の点 $\mathrm{P}(\alpha,~f(\alpha))$ における接線 $\ell$ の方程式を求めよ。
(2) $C$ と $\ell$ の共有点のうち,Pと異なる点をQとするとき,点Qの $x$ 座標を求めよ。

(1)は接線の方程式を求める方法を知っていれば大丈夫なはず。
$f(x)=ax^3+bx^2+cx+d$ より
f'(x)=3ax^2+2bx+c
\end{align*}
&y=(3a\alpha^2+2b\alpha+c)(x-\alpha)+a\alpha^3+b\alpha^2+c\alpha+d \\[4pt]
&y=(3a\alpha^2+2b\alpha+c)x-2a\alpha^3-b\alpha^2+d
\end{align*}

(2)は連立方程式を解けば良い。
$C,~\ell$ の方程式から $y$ を消去すると
&ax^3+bx^2-(3a\alpha^2+2b\alpha)x+2a\alpha^3+b\alpha^2=0~\cdots\cdots(\ast)
\end{align*}

$C$ と $\ell$ は点Pで接しているから,方程式 $(\ast)$ は $x=\alpha$ を重解にもつね。これを利用して賢く因数分解をできるようにしよう。
&a(x-\alpha)^2(x-\beta)=0
\end{align*}
&-a\alpha^2\beta=2a\alpha^3+b\alpha^2 \\[4pt]
&\beta=-2\alpha-\dfrac{b}{a}
\end{align*}
$(\ast)$ を因数分解すると
&a(x-\alpha)^2\left(x+2\alpha+\dfrac{b}{a}\right)=0 \\[4pt]
&x=\alpha,~-2\alpha-\dfrac{b}{a}
\end{align*}
3次関数のグラフの等間隔性

接点Pやもう1つの交点Qの $x$ 座標にどのような関係があるかを調べていこう。
\begin{align*}
ax^3+bx^2-(3a\alpha^2+2b\alpha)x+2a\alpha^3+b\alpha^2=0~\cdots\cdots(\ast)
\end{align*}
2\alpha+\beta=-\dfrac{b}{a}
\end{align*}
\dfrac{2\alpha+\beta}{3}=-\dfrac{b}{3a}~\cdots\cdots①
\end{align*}

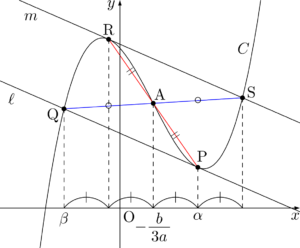
ここで,変曲点をAとすると $x$ 座標が $-\dfrac{b}{3a}$ であることを思い出そう。
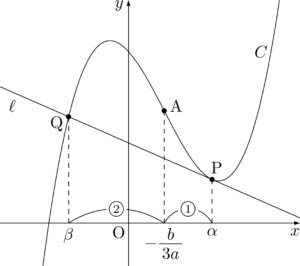

3次関数が変曲点に関して対称であることを考えよう。


3次関数の対称性より,点Rにおける $C$ の接線 $m$ は接線 $\ell$ と平行になる。
1997年 センター数学IIB

3次関数のグラフの等間隔性を利用する練習として,次の問題を解いてみよう。
一般的な解法

まず,接線 $\ell$ の方程式を求める。その後 $y=f(x)$ と連立して,$x$ の方程式を立てる。その方程式の $x=a$ 以外の解が $x=b$ である。

このように考えて解いていこう。
f'(x)=3x^2-\dfrac{4}{3}
\end{align*}
&y=\left(3a^2-\dfrac{4}{3}\right)(x-a)+a^3-\dfrac{4}{3}a \\[4pt]
&y=\left(3a^2-\dfrac{4}{3}\right)x-2a^3
\end{align*}
&x^3-\dfrac{4}{3}x=\left(3a^2-\dfrac{4}{3}\right)x-2a^3 \\[4pt]
&x^3-3a^2x+2a^3=0 \\[4pt]
&(x-a)^2(x+2a)=0 \\[4pt]
&x=a,~-2a
\end{align*}
3次関数の等間隔性を利用した解法

次は3次関数の等間隔性を利用した解法を説明する。
2点A, Bから $x$ 軸に下ろした垂線の足をそれぞれ $\mathrm{H}_1,~\mathrm{H}_2$ とすると,3次関数のグラフの等間隔性より,原点Oは $\mathrm{H}_1\mathrm{H}_2$ を $1:2$ に内分する点となる。
よって,$b=-2a$
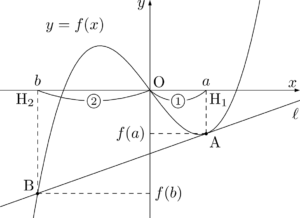

このように,図を描くだけで大した計算もなく,$b=-2a$ と求めることができる。
まとめ

3次関数のグラフの等間隔性を知っていると,接点と変曲点の $x$ 座標が分かっていれば,簡単な計算をするだけで,接線と3次関数のグラフのもう1つの交点の $x$ 座標を求めることができる。

具体的にどのように使うかが難しいので,常に意識しておくことが重要。