インボリュート曲線(伸開線)とは,与えられた曲線に巻きつけられた糸を弛まないように引っ張りながら剥がしていくときの端点が描く曲線である。
例えば,円の伸開線は次のようになる。
また,別の例として,カテナリーの伸開線は次のようになる。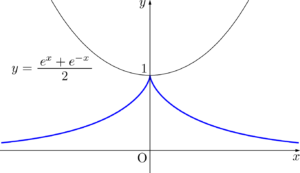
円の伸開線に関する入試問題
\Vec{OP}&=(x(\theta),~y(\theta)) \\[4pt]
&=(\cos\theta,~\sin\theta)+\theta(\cos(\theta+a\pi),~\sin(\theta+a\pi))
\end{align*}
\dint{0}{\alpha}\!\!\!\sqrt{(x'(\theta))^2+(y'(\theta))^2}\;d\theta=b\alpha^c
\end{align*}
b=\dfrac{\myBox{エ}}{\myBox{オ}},~c=\myBox{カ}
\end{align*}
したがって,糸がちょうどほどき終わるまでに点Pのえがく曲線の長さを $d\pi^f$ とすると,
d=\myBox{キ},~f=\myBox{カ}
\end{align*}

1つのベクトルに垂直なベクトルをすぐに作れるようにしよう。
\vec{q}=(-b,~a)
\end{align*}
\vec{q}=\left(\cos\left(\theta+\dfrac{\pi}{2}\right),~\sin\left(\theta+\dfrac{\pi}{2}\right)\right)
\end{align*}

$x$ 成分と $y$ 成分のどちらにマイナスを付けるのか覚えられない人は,複素数平面で考えると良いかもね。
\cos\dfrac{\pi}{2}+i\sin\dfrac{\pi}{2}=i
\end{align*}
(a+bi)i=-b+ai
\end{align*}

符号を変えるのを使うか,角を変えたものを使うかは問題によって変えれば良いね。
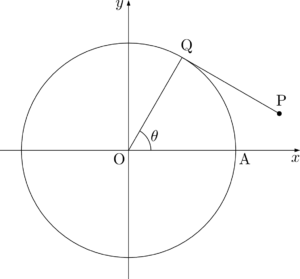
QPの長さは $\ko{\mathrm{AQ}}$ の長さに等しく,扇形OAQの半径は1で,中心角は $\theta$ であるから
\mathrm{QP}=\ko{\mathrm{AQ}}=\theta
\end{align*}
\Vec{OP}&=\Vec{OQ}+\Vec{QP} \\[4pt]
&=(\cos\theta,~\sin\theta)+\theta\left(\cos\left(\theta-\dfrac{\pi}{2}\right),~\sin\left(\theta-\dfrac{\pi}{2}\right)\right)
\end{align*}

次は曲線の長さを求めよう。
\begin{cases}
x(\theta)=\cos\theta+\theta\sin\theta \\[4pt]
y(\theta)=\sin\theta-\theta\cos\theta
\end{cases}
\end{align*}
x'(\theta)&=-\sin\theta+\sin\theta+\theta\cos\theta \\[4pt]
&=\theta\cos\theta \\[4pt]
y'(\theta)&=\cos\theta-\cos\theta+\theta\sin\theta \\[4pt]
&=\theta\sin\theta
\end{align*}
(x'(\theta))^2+(y'(\theta))^2=\theta^2
\end{align*}
L&=\dint{0}{\alpha}\sqrt{(x'(\theta))^2+(y'(\theta))^2}\;d\theta \\[4pt]
&=\dint{0}{\alpha}\theta\;d\theta \\[4pt]
&=\Tint{\dfrac{1}{2}\theta^2}{0}{\alpha} \\[4pt]
&=\dfrac{1}{2}\alpha^2
\end{align*}
これより,糸がちょうどほどき終わるまでに点Pのえがく曲線の長さは $\alpha=2\pi$ を代入して
\dfrac{1}{2}(2\pi)^2=2\pi^2
\end{align*}
カテナリーの伸開線に関する入試問題
f(x)=\dfrac{e^x+e^{-x}}{2}
\end{align*}
(1) $f(x)$ は以下の関係式を満たすことを示せ。
(i) $\{f(x)\}^2-\{f'(x)\}^2=1$
(ii) $f^{\prime\prime}(x)=f(x)$
ただし,$f'(x)$ および $f^{\prime\prime}(x)$ は,それぞれ,$f(x)$ の $x$ に関する1階および2階の導関数を表す。
(2) 曲線 $C$ 上の点 $\mathrm{A}(a,~f(a))$ と点 $\mathrm{B}(0,~f(0))$ の間の曲線の長さ $L$ を求めよ。ただし,$a$ は $a\geqq0$ を満たす定数である。
(3) 点Aにおける曲線 $C$ の接線上に点 $\mathrm{P}(X,~Y)$ をAPの距離が $L$ に等しくなるようにとる。ただし,$X\leqq a$ とする。このとき,$X$ および $Y$ を,$a$ を用いて表せ。
(4) 点Aを動かしたときに点Pの描く曲線を $D$ とする。$a>0$ のとき,曲線 $C$ の点Aにおける接線と曲線 $D$ の点Pにおける接線は常に直交することを示せ。

$f(x)$ を見てカテナリーだと気付けるようにしよう。

(1)(i)は左辺を計算して1になることを示そう。
$f(x)=\dfrac{e^x+e^{-x}}{2}$ より
f'(x)=\dfrac{e^x-e^{-x}}{2}
\end{align*}
\{f(x)\}^2-\{f'(x)\}^2&=\left(\dfrac{e^x+e^{-x}}{2}\right)^2-\left(\dfrac{e^x-e^{-x}}{2}\right)^2 \\[4pt]
&={\color[named]{RoyalBlue}\left(\dfrac{e^x+e^{-x}}{2}+\dfrac{e^x-e^{-x}}{2}\right)\left(\dfrac{e^x+e^{-x}}{2}-\dfrac{e^x-e^{-x}}{2}\right)} \\[4pt]
&=e^{x}\Cdota e^{-x} \\[4pt]
&=1
\end{align*}

青字部分は $(\quad)^2-(\quad)^2$ の因数分解を利用して計算している。

(1)(ii)も左辺を計算して右辺になることを示そう。
$f'(x)=\dfrac{e^x-e^{-x}}{2}$ より
f^{\prime\prime}=\dfrac{e^x+e^{-x}}{2}
\end{align*}

カテナリーの記事では触れていなかったが,(1)の等式はカテナリーの非常に有名な性質。
\sinh x=\dfrac{e^x-e^{-x}}{2},~\cosh x=\dfrac{e^x+e^{-x}}{2}
\end{align*}
\tanh x=\dfrac{\sinh x}{\cosh x}
\end{align*}
&\cosh^2x-\sinh^2x=1 \\[4pt]
&1-\tanh^2x=\dfrac{1}{\cosh^2x} \\[4pt]
&\dfrac{1}{\tanh^2x}-1=\dfrac{1}{\sinh^2x}
\end{align*}
&\dfrac{d}{dx}\sinh x=\cosh x,~~\dfrac{d}{dx}\cosh x=\sinh x \\[4pt]
&\dfrac{d}{dx}\tanh x=\dfrac{1}{\cosh^2x},~~\dfrac{d}{dx}\dfrac{1}{\tanh x}=-\dfrac{1}{\sinh^2x}
\end{align*}

このような高校数学を超えた範囲も知っておくと,入試問題が簡単なものであるように感じるだろう。

曲線の長さの公式を考えたときに,「(1)(i)を再利用できる!」と気付ければ計算量を減らすことができるね。
(1)(i)の結果より
1+\{f'(x)\}^2=\{f(x)\}^2
\end{align*}
L&=\dint{0}{a}\sqrt{1+\{f'(x)\}^2}\;dx \\[4pt]
&=\dint{0}{a}f(x)\;dx \\[4pt]
&=\dint{0}{a}\dfrac{e^x+e^{-x}}{2}\;dx \\[4pt]
&=\Tint{\dfrac{e^x-e^{-x}}{2}}{0}{a} \\[4pt]
&=\dfrac{e^a-e^{-a}}{2}
\end{align*}

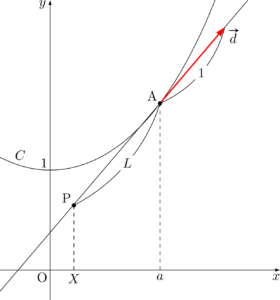
(3)の問題文から伸開線だと分かるね。
点Aにおける接線の単位方向ベクトルを $\vec{d}$ とすると
\vec{d}&=\dfrac{1}{\sqrt{1+\{f'(a)\}^2}}(1,~f'(a)) \\[4pt]
&=\dfrac{1}{f(a)}(1,~f'(a))
\end{align*}
\Vec{OP}&=\Vec{OA}-L\vec{d} \\[4pt]
&=(a,~f(a))-\dfrac{f'(a)}{f(a)}(1,~f'(a))
\end{align*}
したがって
X&=a-\dfrac{f'(a)}{f(a)} \\[4pt]
&=a-\dfrac{e^a-e^{-a}}{e^a+e^{-a}} \\[4pt]
Y&=f(a)-\dfrac{f'(a)}{f(a)}f'(a) \\[4pt]
&=\dfrac{\{f(a)\}^2-\{f'(a)\}^2}{f(a)} \\[4pt]
&=\dfrac{1}{f(a)} \\[4pt]
&=\dfrac{2}{e^a+e^{-a}}
\end{align*}

(3)をベクトルで考えていれば,(4)もベクトルで考えるはずで,内積が0になることを示せば良いんだなと思えるね。

$X,~Y$ が $a$ の関数になっているため,(3)で表した式は曲線 $D$ の媒介変数表示だと捉えることができる。ベクトルの各成分を微分して傾きを表すベクトルを求めよう。
曲線 $D$ 上の点Pにおける接線の方向ベクトルを $\vec{m}$ とすると
\vec{m}=\left(\dfrac{dX}{da},~\dfrac{dY}{da}\right)
\end{align*}
\dfrac{dX}{da}&=1-\dfrac{f^{\prime\prime}f(a)-\{f'(a)\}^2}{\{f(a)\}^2} \\[4pt]
&=1-\dfrac{\{f(a)\}^2-\{f'(a)\}^2}{\{f(a)\}^2} \\[4pt]
&=\dfrac{\{f'(a)\}^2}{\{f(a)\}^2} \\[4pt]
\dfrac{dY}{da}&=-\dfrac{f'(a)}{\{f(a)\}^2}
\end{align*}
\vec{m}&=\dfrac{f'(a)}{\{f(a)\}^2}(f'(a),~-1)
\end{align*}
\vec{d}\Cdota\vec{m}&=\dfrac{1}{f(a)}(1,~f'(a))\Cdota\dfrac{f'(a)}{\{f(a)\}^2}(f'(a),~-1) \\[4pt]
&=0
\end{align*}
まとめ

インボリュート曲線(伸開線)は入試問題によく出るわけではないが,出題されたときに全く手が出ないということがない状態にしておこう。





















