3次関数の対称性（変曲点に関して点対称）と入試問題

Contents

3次関数のグラフが変曲点に関して対称であることの証明

ヒロ

それでは本題。3次関数のグラフが変曲点に関して対称であることを示そう。

例題5$f(x)=ax^3+bx^2+cx+d~(a\neq0)$ とする。例題4の結果を利用して，曲線 $C:y=f(x)$ がある点に関して対称なグラフであることを示せ。

例題4の結果より，点 $(p,~f(p))$ に関して対称なグラフであるとき，$-f(-x+2p)+2f(p)=f(x)$ が成り立つから，$f(x)=ax^3+bx^2+cx+d$ のとき

\begin{align*}
&-f(-x+2p)+2f(p) \\[4pt]
=&-a(-x+2p)^3-b(-x+2p)^2-c(-x+2p)-d+2(ax^3+bx^2+cx+d) \\[4pt]
=&a^3+(-6ap-b)x^2+(12ap^2+4bp+c)x-6ap^3-2bp^2+d
\end{align*}

これが $f(x)$ と一致する条件を考えて

\begin{align*}
\begin{cases}
-6ap-b=b &~\cdots\cdots① \\[4pt]
12ap^2+4bp+c=c &~\cdots\cdots② \\[4pt]
-6ap^3-2bp^2+d=d &~\cdots\cdots③
\end{cases}
\end{align*}

①より $p=-\dfrac{b}{3a}$
このとき $3ap+b=0$ となるから，②の左辺を計算すると

\begin{align*}
4p(3ap+b)+c=c
\end{align*}

となるから②が成り立つ。また③の左辺を計算すると

\begin{align*}
-2p^2(3ap+b)+d=d
\end{align*}

となり③も成り立つ。
よって，曲線 $C$ は点 $\left(-\dfrac{b}{3a},~f\left(-\dfrac{b}{3a}\right)\right)$ に関して対称なグラフである。

点対称であるための条件曲線 $y=f(x)$ が点 $(p,~f(p))$ に関して点対称であるとき

\begin{align*}
2f(p)-f(x)=f(2p-x)
\end{align*}

が成り立つ。

ヒロ

文字の並びが覚えやすい感じだね。

変曲点の定義と求め方

ヒロ

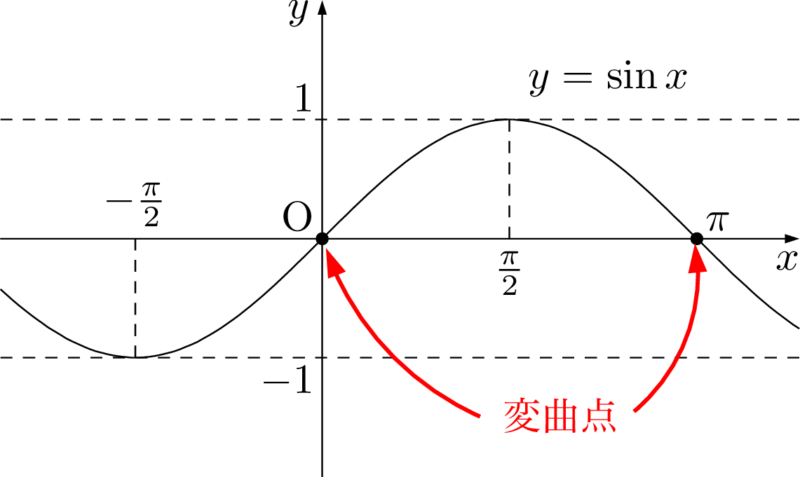
例えば，アルファベットのS（エス）は点対称の文字で，対称の中心で曲がり方が変わっている。$y=\sin x$ のグラフでは原点で曲がり方が変わっている。

ヒロ

文系生は，アルファベットのSにあるような曲がり方が変わる点を変曲点と呼ぶんだということを覚えておこう。

もう少し丁寧に言うと「曲がり方が変わる」というのは「凹凸が変わる」ということである。$y=\sin x$ のグラフの原点の近傍の $x<0$ の部分では下に凸になっていて，$x>0$ の部分では上に凸になっているから，原点は変曲点である。また，$x=\pi$ の前後でも凹凸が変わるから，点 $(\pi,~0)$ も変曲点である。