Contents
点Pに関して対称なグラフの方程式

ヒロ
次は,ある点に関して対称なグラフの方程式を考えよう。
例題2$f(x)=(x-5)^2+3$ とし,点Pの座標を $(3,~2)$ とする。点Pに関して $y=f(x)$ のグラフ $C$ と対称なグラフ $D$ の方程式を求めよ。

ヒロ
$C$ の頂点に着目して考えよう。
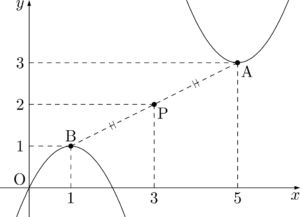
$C$ の頂点をAとすると,$\mathrm{A}(5,~3)$ であり,$D$ の頂点を $\mathrm{B}(a,~b)$ とすると,点Bは線分APを $2:1$ に外分する点であるから
\begin{align*}
&a=2\Cdota3-5=1 \\[4pt]
&b=2\Cdota2-3=1
\end{align*}
$D$ の $x^2$ の係数は $-1$ になるから $D$ の方程式は&a=2\Cdota3-5=1 \\[4pt]
&b=2\Cdota2-3=1
\end{align*}
\begin{align*}
y=-(x-1)^2+1
\end{align*}
y=-(x-1)^2+1
\end{align*}


ヒロ
放物線の性質を考えず,一般的な曲線でも使える考え方をすると,次のようになる。
点 $\mathrm{P}(3,~2)$ に関して $C$ 上の点 $\mathrm{A}(x,~y)$ と対称な点を $\mathrm{B}(X,~Y)$ とすると,点Aは線分BPを $2:1$ に外分する点であるから
\begin{align*}
x=-X+6\,,~~y=-Y+4
\end{align*}
となるから,$y=f(x)$ に代入してx=-X+6\,,~~y=-Y+4
\end{align*}
\begin{align*}
&-Y+4=(-X+6-5)^2+3 \\[4pt]
&Y=-(X-1)^2+1
\end{align*}
&-Y+4=(-X+6-5)^2+3 \\[4pt]
&Y=-(X-1)^2+1
\end{align*}
点対称なグラフとは?【奇関数と偶関数】

ヒロ
曲線 $C$ が点Pに関して点対称であるとき,「点Pに関して $C$ 上の任意の点と対称な点もまた $C$ 上にある」と考えることができる。

ヒロ
話を簡単にするために,まずは,グラフが原点に関して点対称であるとき,どのようなことが言えるかを考えよう。
例題3原点に関して曲線 $C:y=f(x)$ と対称なグラフの方程式を求めよ。
原点に関して $C$ 上の点 $\mathrm{A}(x,~y)$ と対称な点を $\mathrm{B}(X,~Y)$ とすると
\begin{align*}
x=-X\,,~~y=-Y
\end{align*}
となるから,$y=f(x)$ に代入してx=-X\,,~~y=-Y
\end{align*}
\begin{align*}
&-Y=f(-X) \\[4pt]
&Y=-f(-X)
\end{align*}
よって,求めるグラフの方程式は&-Y=f(-X) \\[4pt]
&Y=-f(-X)
\end{align*}
\begin{align*}
y=-f(-x)
\end{align*}
y=-f(-x)
\end{align*}

ヒロ
ここで奇関数と偶関数について簡単に説明しておく。
奇関数と偶関数グラフが原点に関して点対称である関数 $f(x)$ を奇関数といい,$f(-x)=-f(x)$ が成り立つ。また,グラフが $y$ 軸に関して線対称である関数 $g(x)$ を偶関数といい,$g(-x)=g(x)$ が成り立つ。$y=x^n~$$(nは整数)$ で表される関数では,$n$ が偶数のときは偶関数,$n$ が奇数のときは奇関数となる。

ヒロ
他の身近な奇関数と偶関数としては,次のようなものがある。
$f(x)=a\sin x~(a>0)$ のときは
\begin{align*}
f(-x)=a\sin(-x)=-a\sin x
\end{align*}
となり,$f(-x)=-f(x)$ が成り立つから奇関数である。確かに $y=a\sin x$ のグラフは原点に関して点対称になっている。f(-x)=a\sin(-x)=-a\sin x
\end{align*}

$f(x)=a\cos x$ のときは
\begin{align*}
f(-x)=a\cos x=a\cos x
\end{align*}
となり,$f(-x)=f(x)$ が成り立つから偶関数である。確かに $y=a\cos x$ のグラフは $y$ 軸に関して線対称になっている。f(-x)=a\cos x=a\cos x
\end{align*}


ヒロ
$a<0$ のときのグラフを描くのが面倒だから $a>0$ としたけど,$a<0$ でも奇関数・偶関数の話には影響しないからね。

ヒロ
話を点対称に戻そう。次の問題を考えよう。
例題4点 $\mathrm{P}(p,~q)$ に関して曲線 $C:y=f(x)$ と対称なグラフの方程式を求めよ。
点Pに関して $C$ 上の点 $\mathrm{A}(x,~y)$ と対称な点を $\mathrm{B}(X,~Y)$ とすると
\begin{align*}
x=-X+2p\,,~~y=-Y+2q
\end{align*}
となるから,$y=f(x)$ に代入してx=-X+2p\,,~~y=-Y+2q
\end{align*}
\begin{align*}
&-Y+2q=f(-X+2p) \\[4pt]
&Y=-f(-X+2p)+2q
\end{align*}
よって,求めるグラフの方程式&-Y+2q=f(-X+2p) \\[4pt]
&Y=-f(-X+2p)+2q
\end{align*}
\begin{align*}
y=-f(-x+2p)+2q
\end{align*}
y=-f(-x+2p)+2q
\end{align*}

ヒロ
点Pが $C$ 上にあり,$y=-f(-x+2p)+2q$ が $y=f(x)$ と一致するとき,曲線 $C$ は点Pに関して対称なグラフだと言えることが分かったね。