Contents
$x^2$ の係数が等しい共通接線を求める問題【2019年 明治薬科大】

ヒロ
それでは,次の入試問題を解いてみよう。
2019年 明治薬科大次の $\myhako$ にあてはまる答を解答欄に記入しなさい。
$a$ を正の定数とする。放物線 $C_1:y=x^2$ を $x$ 軸方向に4,$y$ 軸方向に $8a$ だけ平行移動した放物線を $C_2$ とすると $C_2$ の方程式は $y=\myBox{(a)}$ となり,$C_1$ と $C_2$ の交点の $x$ 座標は $x=\myBox{(b)}$ である。
次に,2つの放物線 $C_1$ と $C_2$ の両方に接する直線を $l$ とする。$C_1$ と $l$ の接点の $x$ 座標は $x=\myBox{(c)}$ ,$C_2$ と $l$ の接点の $x$ 座標は $x=\myBox{(d)}$ であり,$l$ の方程式は $y=\myBox{(e)}$ となる。
よって,$C_1,~C_2$ および $l$ で囲まれる部分の面積 $S$ は $S=\myBox{(f)}$ となる。
$a$ を正の定数とする。放物線 $C_1:y=x^2$ を $x$ 軸方向に4,$y$ 軸方向に $8a$ だけ平行移動した放物線を $C_2$ とすると $C_2$ の方程式は $y=\myBox{(a)}$ となり,$C_1$ と $C_2$ の交点の $x$ 座標は $x=\myBox{(b)}$ である。
次に,2つの放物線 $C_1$ と $C_2$ の両方に接する直線を $l$ とする。$C_1$ と $l$ の接点の $x$ 座標は $x=\myBox{(c)}$ ,$C_2$ と $l$ の接点の $x$ 座標は $x=\myBox{(d)}$ であり,$l$ の方程式は $y=\myBox{(e)}$ となる。
よって,$C_1,~C_2$ および $l$ で囲まれる部分の面積 $S$ は $S=\myBox{(f)}$ となる。

ヒロ
空欄を埋めるのに特化した解法を説明する。
【(a)(b)の解答】
$C_1$ を $x$ 軸方向に4,$y$ 軸方向に $8a$ だけ平行移動した放物線が $C_2$ だから
$C_1$ を $x$ 軸方向に4,$y$ 軸方向に $8a$ だけ平行移動した放物線が $C_2$ だから
\begin{align*}
C_2:y=(x-4)^2+8a
\end{align*}
$C_1:y=x^2$ と連立させて $y$ を消去するとC_2:y=(x-4)^2+8a
\end{align*}
\begin{align*}
&x^2=(x-4)^2+8a \\[4pt]
&4(2x-4)=8a \\[4pt]
&x=a+2
\end{align*}
&x^2=(x-4)^2+8a \\[4pt]
&4(2x-4)=8a \\[4pt]
&x=a+2
\end{align*}

ヒロ
ここで2次方程式を解く際に,平方の差を使っていることにも注意しておこう。
$(\quad\quad)^2-(\quad\quad)^2$ を計算するときには,因数分解公式
\begin{align*}
a^2-b^2=(a+b)(a-b)
\end{align*}
を利用するのが速い。今回問題では次のようにしている。a^2-b^2=(a+b)(a-b)
\end{align*}
\begin{align*}
x^2-(x-4)^2&=\{x-(x-4)\}\{x+(x-4)\} \\[4pt]
&=4(2x-4)
\end{align*}
x^2-(x-4)^2&=\{x-(x-4)\}\{x+(x-4)\} \\[4pt]
&=4(2x-4)
\end{align*}
【(c)~(e)の解答】
$C_2$ の頂点をPとすると,平行移動量より,直線OPの傾き $m$ は
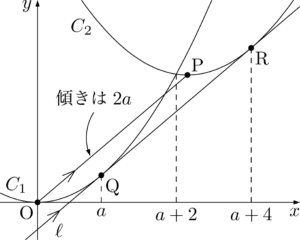
$C_2$ の頂点をPとすると,平行移動量より,直線OPの傾き $m$ は
\begin{align*}
m=\dfrac{8a}{4}=2a
\end{align*}
2つの放物線 $C_1,~C_2$ の $x^2$ の係数が等しいから,共通接線 $l$ は直線OPと平行であるから,$l$ の傾きも $2a$ である。$y=x^2$ より $y’=2x$ となるから,$C_1$ と $l$ の接点の $x$ 座標を $t$ とするとm=\dfrac{8a}{4}=2a
\end{align*}
\begin{align*}
&2t=2a \\[4pt]
&t=a
\end{align*}
接点も $x$ 軸方向に4,$y$ 軸方向に $8a$ だけ平行移動されるから,$C_2$ と $l$ の接点の $x$ 座標は $a+4$ である。$l$ は点 $(a,~a^2)$ を通り,傾き $2a$ の直線であるから,その方程式は&2t=2a \\[4pt]
&t=a
\end{align*}
\begin{align*}
y=2ax-a^2
\end{align*}
y=2ax-a^2
\end{align*}


ヒロ
最後の面積は3分の1公式で処理できる。
【(f)の解答】
$C_1,~C_2,~l$ で囲まれる部分は図の斜線部分である。
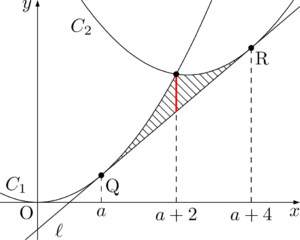
斜線部分を直線 $x=a+2$ で分割して3分の1公式を利用して面積を求めると,次のようになる。
$C_1,~C_2,~l$ で囲まれる部分は図の斜線部分である。

斜線部分を直線 $x=a+2$ で分割して3分の1公式を利用して面積を求めると,次のようになる。
\begin{align*}
S&=\dfrac{1}{3}\Cdota2^3+\dfrac{1}{3}\Cdota2^3 \\[4pt]
&=\dfrac{16}{3}
\end{align*}
S&=\dfrac{1}{3}\Cdota2^3+\dfrac{1}{3}\Cdota2^3 \\[4pt]
&=\dfrac{16}{3}
\end{align*}

ヒロ
$x^2$ の係数が等しいから,12分の1公式を利用して求めても良い。
接点間の幅が4だから
\begin{align*}
S=\dfrac{1}{12}\Cdota4^3=\dfrac{16}{3}
\end{align*}
S=\dfrac{1}{12}\Cdota4^3=\dfrac{16}{3}
\end{align*}

ヒロ
微分を利用する点では,通常の解法とは変わらないが,共通接線の傾きが予め分かっているから,かなり楽になるね。

ヒロ
また,3分の1公式や12分の1公式を利用することで,面積を速く求めることができるところも見逃せない。


















