【数学ⅡB】直径の両端が定められた円の方程式【西南学院大・東京電機大】

円の方程式を求める問題では，最初に与えられる条件は色々なパターンがあります。

その中でも今回は，直径の両端が定められた円の方程式について説明します。

良く出題される問題なので，確実にできるようにしましょう。

余裕があれば，素早く求める方法もマスターしましょう。

直径の両端が与えられた円の方程式

ヒロ

公式として覚える人は次のことを覚えよう。

直径の両端が与えられた円2点A$(a,~b)$，B$(c,~d)$ を直径の両端とする円の方程式は

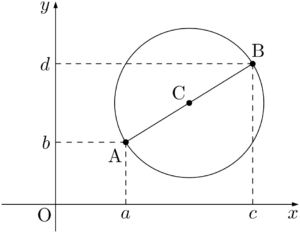
\begin{align*}
(x-a)(x-c)+(y-b)(y-d)=0
\end{align*}

と表される。基本形に変形すると

\begin{align*}
\left(x-\dfrac{a+c}{2}\right)^2+\left(y-\dfrac{b+d}{2}\right)^2=\dfrac{(a-c)^2+(b-d)^2}{4}
\end{align*}

となる。

ヒロ

何故，このように表されるかについて説明していく。