「組合せ」に関する問題を解く練習をしましょう。
問題文に「選ぶ」という言葉があれば分かりやすいかもしれませんが,すべての問題に「選ぶ」と書かれているわけではありません。
問題文をしっかり読んで適切に対応することが必要です。
様々な問題がありますが,ここでは三角形の個数を求める有名問題を考えてみよう。
Contents
三角形の個数を求める問題
問題正八角形の3つの頂点を結んでできる三角形について次の個数を求めよ。
(1) 三角形の総数
(2) 正八角形と2辺を共有する三角形
(3) 正八角形と1辺を共有する三角形
(4) 正八角形と1辺も共有しない三角形
(1) 三角形の総数
(2) 正八角形と2辺を共有する三角形
(3) 正八角形と1辺を共有する三角形
(4) 正八角形と1辺も共有しない三角形

ヒロ
何を決めれば三角形が1つ決まるのかを考えよう。
【(1)の考え方と解答】
正八角形の8個の頂点から,どの3個の頂点を選んだとしても一直線上に並ぶことはないから,3個の頂点を選んだ時点でそれらを結んでできる三角形が1つできる。
したがって,8個の頂点から3個の頂点を選ぶ方法の総数が求める三角形の総数であるから
正八角形の8個の頂点から,どの3個の頂点を選んだとしても一直線上に並ぶことはないから,3個の頂点を選んだ時点でそれらを結んでできる三角形が1つできる。
したがって,8個の頂点から3個の頂点を選ぶ方法の総数が求める三角形の総数であるから
\begin{align*}
\nCk{8}{3}&=\dfrac{8\Cdot7\Cdot6}{3\Cdot2\Cdot1} \\[4pt]&=56~個
\end{align*}
\nCk{8}{3}&=\dfrac{8\Cdot7\Cdot6}{3\Cdot2\Cdot1} \\[4pt]&=56~個
\end{align*}

ヒロ
もし,ある3個の頂点を選んだときに一直線上に並ぶことがあるなら,その分を除かないといけないことに注意しよう。
(2) 正八角形と2辺を共有する三角形
【(2)の考え方と解答】
正八角形と2辺を共有する三角形は,正八角形と1つの角を共有する三角形であると考えることができる。
例えば2辺AB, AHを共有する三角形は $\kaku{A}$ を共有する三角形と見ることができる。
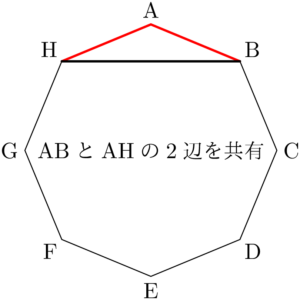
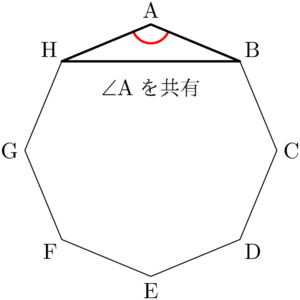
つまり,共有する角を1つ決めることで,2辺を共有する三角形が1つ決まることが分かる。
正八角形には8個の角があるから,求める三角形の個数は8個である。
正八角形と2辺を共有する三角形は,正八角形と1つの角を共有する三角形であると考えることができる。
例えば2辺AB, AHを共有する三角形は $\kaku{A}$ を共有する三角形と見ることができる。


つまり,共有する角を1つ決めることで,2辺を共有する三角形が1つ決まることが分かる。
正八角形には8個の角があるから,求める三角形の個数は8個である。
(3) 正八角形と1辺を共有する三角形
【(3)の考え方と解答】
正八角形と1辺を共有する三角形は,次の2つの手順でただ1つに決まる。
① 共有する1辺を選ぶ。
② 共有する辺が含む頂点とその隣の頂点を除く4つの頂点から残りの1点を選ぶ。
例えば辺ABを共有すると決めると,その時点で2つの頂点を選んだことになる。あと1つの頂点を決めると三角形ができるが,共有辺ABの隣の頂点C, Hを選んでしまうと2辺を共有する三角形になる。したがって,残りの頂点はD, E, F, Gの4つから選ぶことになる。
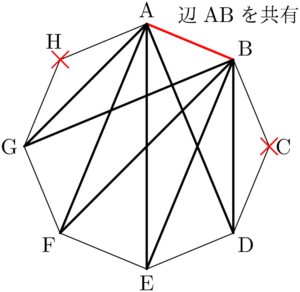
①の方法は8通りあり,②の方法は4通りあるから,求める三角形の個数は
正八角形と1辺を共有する三角形は,次の2つの手順でただ1つに決まる。
① 共有する1辺を選ぶ。
② 共有する辺が含む頂点とその隣の頂点を除く4つの頂点から残りの1点を選ぶ。
例えば辺ABを共有すると決めると,その時点で2つの頂点を選んだことになる。あと1つの頂点を決めると三角形ができるが,共有辺ABの隣の頂点C, Hを選んでしまうと2辺を共有する三角形になる。したがって,残りの頂点はD, E, F, Gの4つから選ぶことになる。

①の方法は8通りあり,②の方法は4通りあるから,求める三角形の個数は
\begin{align*}
8\times4-32~個
\end{align*}
8\times4-32~個
\end{align*}
(4) 正八角形と1辺も共有しない三角形
【(4)の考え方と解答】
正八角形と1辺も共有しない三角形を具体的に考えると,$\sankaku{ACF}$ などがある。

何を決めると正八角形と辺を共有しない三角形が決まるかと考えても中々進まない。
そういうときは考え方を変える。直接求めることが難しいときは,余事象を考えてみよう。つまり,正八角形と辺を共有する三角形に着目しよう。
三角形の辺はその名の通り,3つあるのだから,最大でも共有する辺の本数は3本である。しかし,正八角形と3つの辺を共有して三角形を作ることは不可能だということはすぐに分かるはず。つまり,共有する辺は1本か2本のどちらかになる。そして,これらの三角形の個数は(2)と(3)で求めている。三角形が全部で何個できるかについても(1)で求めているから,あとは簡単な引き算をするだけだね。求める三角形の個数は
正八角形と1辺も共有しない三角形を具体的に考えると,$\sankaku{ACF}$ などがある。

何を決めると正八角形と辺を共有しない三角形が決まるかと考えても中々進まない。
そういうときは考え方を変える。直接求めることが難しいときは,余事象を考えてみよう。つまり,正八角形と辺を共有する三角形に着目しよう。
三角形の辺はその名の通り,3つあるのだから,最大でも共有する辺の本数は3本である。しかし,正八角形と3つの辺を共有して三角形を作ることは不可能だということはすぐに分かるはず。つまり,共有する辺は1本か2本のどちらかになる。そして,これらの三角形の個数は(2)と(3)で求めている。三角形が全部で何個できるかについても(1)で求めているから,あとは簡単な引き算をするだけだね。求める三角形の個数は
\begin{align*}
&(全体)-((2辺共有)+(1辺共有)) \\[4pt]&=56-(8+32) \\[4pt]&=16
\end{align*}
&(全体)-((2辺共有)+(1辺共有)) \\[4pt]&=56-(8+32) \\[4pt]&=16
\end{align*}
三角形の個数を求める問題2
問題正八角形の3つの頂点を結んでできる三角形について次の個数を求めよ。
(1) 直角三角形
(2) 鈍角三角形
(3) 正三角形でない二等辺三角形
(4) 3辺の長さがすべて異なる三角形
(1) 直角三角形
(2) 鈍角三角形
(3) 正三角形でない二等辺三角形
(4) 3辺の長さがすべて異なる三角形

ヒロ
正八角形に外接する円を描くと,直角三角形になるための条件が見えるはず。
【(1)の考え方と解答】
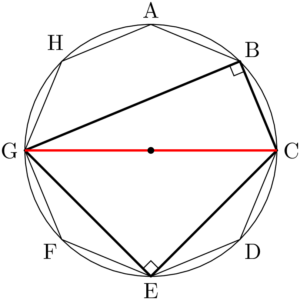
正八角形の外接円を描くと次のようになる。円の中心は対角線CGの中点である。
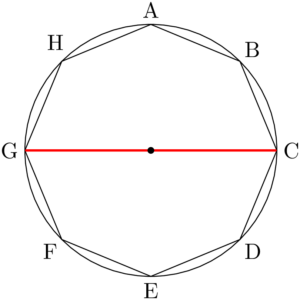
正八角形の外接円を描くと次のようになる。円の中心は対角線CGの中点である。


ヒロ
次の記事でも触れているが,直径に対する円周角が直角であることを思い出そう。
例えば直径としてCGを選ぶと,残りの6つの頂点のどれを選んでも直角三角形ができる。
つまり,次の2つの手順で直角三角形になる3点を選ぶことができる。
① 直径を選ぶ。
② 直径の両端以外の6つの頂点から,1つの頂点を選ぶ。
①の方法はAE, BF, CG, DHの4通り。②の方法は6通り。よって,求める直角三角形の個数は

つまり,次の2つの手順で直角三角形になる3点を選ぶことができる。
① 直径を選ぶ。
② 直径の両端以外の6つの頂点から,1つの頂点を選ぶ。
①の方法はAE, BF, CG, DHの4通り。②の方法は6通り。よって,求める直角三角形の個数は
\begin{align*}
4\times6=24~個
\end{align*}
4\times6=24~個
\end{align*}
(2) 鈍角三角形
【(2)の考え方と解答】
直角三角形のときと同じように外接円を利用して考える。
当たり前のことであるが,鈍角三角形は1つの角だけが鈍角である。2つの角が鈍角ということはあり得ない。
したがって,最長辺を決めるとその対角が鈍角になる。
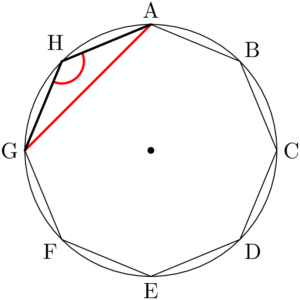
例えば点Aを通る辺のうち,最長辺をAGとすると,鈍角の頂点の選び方はHの1通り。
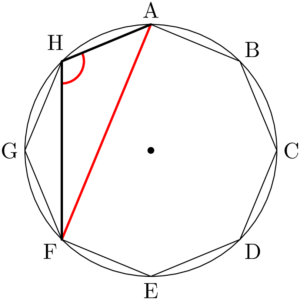
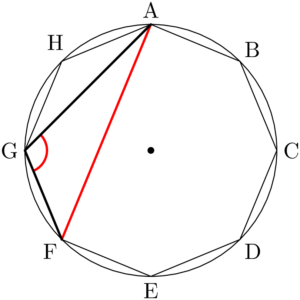
また最長辺がAFのときは,鈍角の頂点はG, Hの2通りある。
次の2つの手順で鈍角三角形を作ることができる。
① 最長辺の一端となる頂点を決める。
② 最長辺のもう1つの端点を決める。
② 鈍角の頂点を決める。
①の方法は8通り(仮に点Aと選んだとする)。②の決め方によって③の決め方が異なることに注意する。
②で点Gを選ぶと,③は1通り。②で点Fを選ぶと,③は2通り。
したがって,求める鈍角三角形の個数は
直角三角形のときと同じように外接円を利用して考える。
当たり前のことであるが,鈍角三角形は1つの角だけが鈍角である。2つの角が鈍角ということはあり得ない。
したがって,最長辺を決めるとその対角が鈍角になる。
例えば点Aを通る辺のうち,最長辺をAGとすると,鈍角の頂点の選び方はHの1通り。

また最長辺がAFのときは,鈍角の頂点はG, Hの2通りある。


次の2つの手順で鈍角三角形を作ることができる。
① 最長辺の一端となる頂点を決める。
② 最長辺のもう1つの端点を決める。
② 鈍角の頂点を決める。
①の方法は8通り(仮に点Aと選んだとする)。②の決め方によって③の決め方が異なることに注意する。
②で点Gを選ぶと,③は1通り。②で点Fを選ぶと,③は2通り。
したがって,求める鈍角三角形の個数は
\begin{align*}
8\times(1+2)=24~個
\end{align*}
8\times(1+2)=24~個
\end{align*}

ヒロ
鈍角の頂点に着目する考え方もある。
【別解】
次の手順で鈍角三角形を作ることができる。
① 鈍角の頂点を決める。
② 鈍角の対辺を決める。
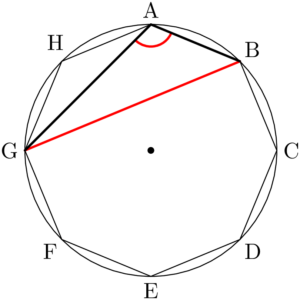
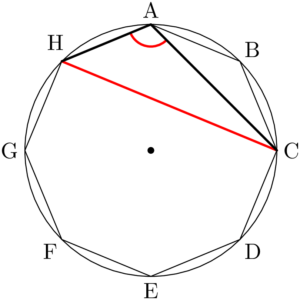
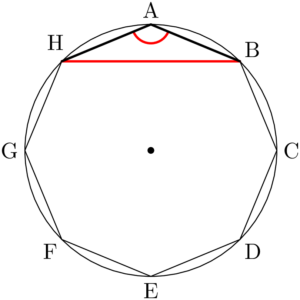
例えば①で点Aを選んだとする。②はBG, CH, BHの3通りある。
①の方法は8通りある。②の方法は3通りあるから,求める鈍角三角形の個数は
次の手順で鈍角三角形を作ることができる。
① 鈍角の頂点を決める。
② 鈍角の対辺を決める。
例えば①で点Aを選んだとする。②はBG, CH, BHの3通りある。



①の方法は8通りある。②の方法は3通りあるから,求める鈍角三角形の個数は
\begin{align*}
8\times3=24~個
\end{align*}
8\times3=24~個
\end{align*}
(3) 正三角形でない二等辺三角形
【(3)の考え方と解答】
この問題では,正三角形を作ることはできない。
二等辺三角形を考えるときは,底辺が水平になるようにすると考えやすい。次の手順で二等辺三角形を作ることができる。
① 頂点を決める。
② 底辺を決める。
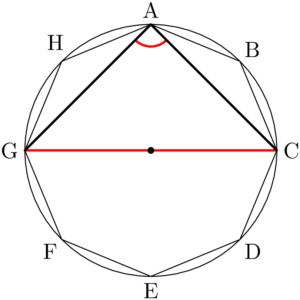
例えば①で点Aを選んだとすると,②はBH, CG, DFの3通りある。

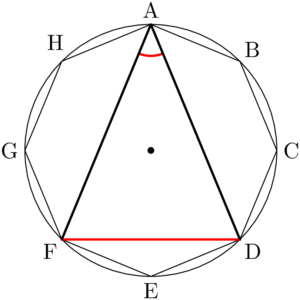
①の方法は8通りあり,②の方法は3通りあるから,求める二等辺三角形の個数は
この問題では,正三角形を作ることはできない。
二等辺三角形を考えるときは,底辺が水平になるようにすると考えやすい。次の手順で二等辺三角形を作ることができる。
① 頂点を決める。
② 底辺を決める。
例えば①で点Aを選んだとすると,②はBH, CG, DFの3通りある。



①の方法は8通りあり,②の方法は3通りあるから,求める二等辺三角形の個数は
\begin{align*}
8\times3=24~個
\end{align*}
8\times3=24~個
\end{align*}
(4) 3辺の長さがすべて異なる三角形
【(4)の考え方と解答】
辺の長さに着目すると,3辺が等しいときは正三角形になり,2辺が等しいときは二等辺三角形になる。どちらでもないときが今回求める三角形ということになる。
この問題では,正三角形を作ることはできない。また,二等辺三角形の個数は(3)で求めた24個。作ることができる三角形は全部で
辺の長さに着目すると,3辺が等しいときは正三角形になり,2辺が等しいときは二等辺三角形になる。どちらでもないときが今回求める三角形ということになる。
この問題では,正三角形を作ることはできない。また,二等辺三角形の個数は(3)で求めた24個。作ることができる三角形は全部で
\begin{align*}
\nCk{8}{3}=56~個
\end{align*}
であるから,求める三角形の個数は\nCk{8}{3}=56~個
\end{align*}
\begin{align*}
56-24=32~個
\end{align*}
56-24=32~個
\end{align*}





















