この記事では,3次関数の極大値と極小値の差を簡単に求める方法を説明します。
極値の差の公式を使うことで,答えだけを求めれば良い試験において,時間を短縮することができて,試験で有利になります。
3次関数の極値の差の公式

ヒロ
極大と極小をもつ3次関数において,極値の差を簡単に求めることができる公式を覚えておこう。
プリントを次のリンクからダウンロードできます。
3次関数 $C:y=f(x)=ax^3+bx^2+cx+d~(a>0)$ が $x=\alpha,~\beta$ で極値をとるとすると,そのグラフは次のようになる。
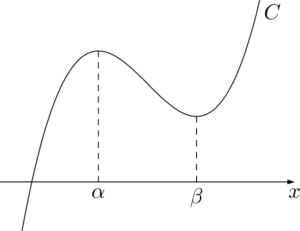
導関数を求めると
つまり,極値をとる $x$ 座標と $x^3$ の係数から,3次関数の差を求めることができる。

導関数を求めると
\begin{align*}
f'(x)=3ax^2+2bx+c
\end{align*}
となり,$f(\alpha)=0$,$f(\beta)=0$ であるから,$f'(x)$ はf'(x)=3ax^2+2bx+c
\end{align*}
\begin{align*}
f'(x)=3a(x-\alpha)(x-\beta)
\end{align*}
と因数分解できる。よって,f'(x)=3a(x-\alpha)(x-\beta)
\end{align*}
\begin{align*}
f(\alpha)-f(\beta)&=\dint{\beta}{\alpha}f'(x)\,dx \\[4pt]
&=\dint{\beta}{\alpha}3a(x-\alpha)(x-\beta)\,dx \\[4pt]
&=-\dfrac{3a}{6}(\alpha-\beta)^3 \\[4pt]
&=\dfrac{1}{2}a(\beta-\alpha)^3
\end{align*}
が成り立つ。f(\alpha)-f(\beta)&=\dint{\beta}{\alpha}f'(x)\,dx \\[4pt]
&=\dint{\beta}{\alpha}3a(x-\alpha)(x-\beta)\,dx \\[4pt]
&=-\dfrac{3a}{6}(\alpha-\beta)^3 \\[4pt]
&=\dfrac{1}{2}a(\beta-\alpha)^3
\end{align*}
つまり,極値をとる $x$ 座標と $x^3$ の係数から,3次関数の差を求めることができる。
1994年 センター数学IIB

ヒロ
それでは,1994年のセンター試験を解いてみよう。
1994年 センター試験 本試験3次関数 $f(x)=x^3+px^2+qx+r$ は $x=0$ で極大,$x=m$ で極小となり,極小値は0であるとする。このとき,
\begin{align*}
p=-\dfrac{\myBox{ア}}{\myBox{イ}}m,~~q=\myBox{ウ}
\end{align*}
であり,$f(x)$ は,p=-\dfrac{\myBox{ア}}{\myBox{イ}}m,~~q=\myBox{ウ}
\end{align*}
\begin{align*}
f(x)=(x-m)^2\left(x+\dfrac{m}{\myBox{エ}}\right)
\end{align*}
と因数分解できる。f(x)=(x-m)^2\left(x+\dfrac{m}{\myBox{エ}}\right)
\end{align*}
一般的な解法

ヒロ
まずは一般的な解法の説明をする。問題文に極値に関する情報があれば,次のポイントを利用しよう。
極値から分かること関数 $f(x)$ が $x=p$ で極値 $q$ をとるとき
\begin{align*}
f(p)=q\,,~~f'(p)=0
\end{align*}
が成り立つ。f(p)=q\,,~~f'(p)=0
\end{align*}
$f(x)=x^3+px^2+qx+r$ より
これを因数分解して
\begin{align*}
f'(x)=3x^2+2px+q
\end{align*}
$x=0,~m$ で極値をとるから $f'(0)=f'(m)=0$ が成り立つ。よってf'(x)=3x^2+2px+q
\end{align*}
\begin{align*}
\begin{cases}
f'(0)=q=0 &~\cdots\cdots①\\[4pt]
f'(m)=3m^2+2pm+q=0 &~\cdots\cdots②
\end{cases}
\end{align*}
①を②に代入すると\begin{cases}
f'(0)=q=0 &~\cdots\cdots①\\[4pt]
f'(m)=3m^2+2pm+q=0 &~\cdots\cdots②
\end{cases}
\end{align*}
\begin{align*}
&3m^2+2pm=0 \\[4pt]
&m(3m+2p)=0
\end{align*}
$m\neq0$ であるから,&3m^2+2pm=0 \\[4pt]
&m(3m+2p)=0
\end{align*}
\begin{align*}
&3m+2p=0 \\[4pt]
&p=-\dfrac{3}{2}m
\end{align*}
さらに極小値が0であるから&3m+2p=0 \\[4pt]
&p=-\dfrac{3}{2}m
\end{align*}
\begin{align*}
&f(m)=0 \\[4pt]
&m^3+pm^2+qm+r=0 \\[4pt]
&m^3-\dfrac{3}{2}m^3+r=0 \\[4pt]
&r=\dfrac{1}{2}m^3
\end{align*}
よって,$f(x)=x^3-\dfrac{3}{2}mx^2+\dfrac{1}{2}m^3$&f(m)=0 \\[4pt]
&m^3+pm^2+qm+r=0 \\[4pt]
&m^3-\dfrac{3}{2}m^3+r=0 \\[4pt]
&r=\dfrac{1}{2}m^3
\end{align*}
これを因数分解して
\begin{align*}
f(x)=(x-m)^2\left(x+\dfrac{m}{2}\right)
\end{align*}
f(x)=(x-m)^2\left(x+\dfrac{m}{2}\right)
\end{align*}
3次関数の性質を利用した解法

ヒロ
次は,3次関数の等間隔性と極値の差の公式を利用した解法を説明する。
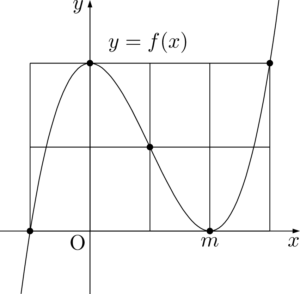
まずは,下図のように長方形を描いて,縦2個×横4個になるように8等分する。
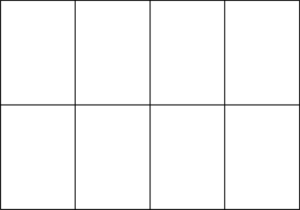
$x^3$ の係数が正なので,下図のように5つの点をとって3次関数のグラフを描く。
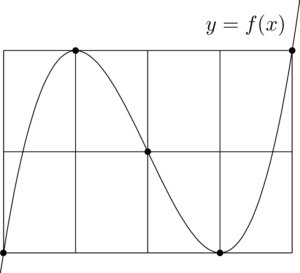

$x^3$ の係数が正なので,下図のように5つの点をとって3次関数のグラフを描く。


ヒロ
次は極値の情報を反映させよう。
$x=0$ で極大,$x=m$ で極小だから次のようになる。
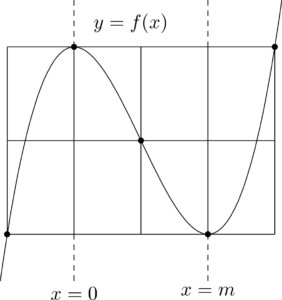
直線 $x=0$ が $y$ 軸であることと,極小値が0であることを考えると次のようになる。

直線 $x=0$ が $y$ 軸であることと,極小値が0であることを考えると次のようになる。


ヒロ
この図から分かることを書き込んでいこう。
等間隔性から変曲点の $x$ 座標は $\dfrac{m}{2}$ と分かる。つまり,
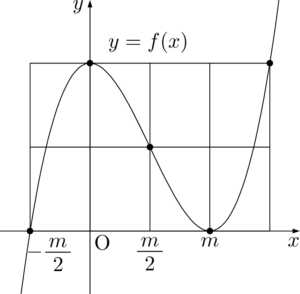
グラフより
また,$y=x^3+px^2+qx+r$ 上の点 $(0,~r)$ における接線の方程式は $y=qx+r$ であり,$x=0$ で極大であることを考えると,$q=0$ と分かる。
\begin{align*}
&-\dfrac{p}{3}=\dfrac{m}{2} \\[4pt]
&p=-\dfrac{3}{2}m
\end{align*}
と求めることができる。さらに,$y=f(x)$ のグラフと $x$ 軸の交点の $x$ 座標は $m$ と $-\dfrac{m}{2}$ であることも分かる。&-\dfrac{p}{3}=\dfrac{m}{2} \\[4pt]
&p=-\dfrac{3}{2}m
\end{align*}

グラフより
\begin{align*}
f(x)=(x-m)^2\left(x+\dfrac{m}{2}\right)
\end{align*}
となることが分かる。f(x)=(x-m)^2\left(x+\dfrac{m}{2}\right)
\end{align*}
また,$y=x^3+px^2+qx+r$ 上の点 $(0,~r)$ における接線の方程式は $y=qx+r$ であり,$x=0$ で極大であることを考えると,$q=0$ と分かる。

ヒロ
ここで,次の接線の方程式の求め方を理解して使えるようにしておこう。
接線の方程式$f(x)=ax^3+bx^2+cx+d$ とすると
\begin{align*}
f(x)=x^2(ax+b)+cx+d
\end{align*}
これは $y=f(x)$ 上の点 $(0,~f(0))$ における接線の方程式は $y=cx+d$ であり,接点以外の交点の $x$ 座標が $-\dfrac{b}{a}$ であることを表している。f(x)=x^2(ax+b)+cx+d
\end{align*}
$x^3$ の係数が1だから,極値の差の公式より $r=\dfrac{1}{2}m^3$ となる。
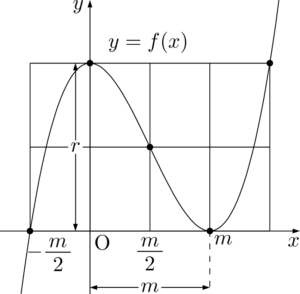

3次関数の極値の差の公式のまとめ

ヒロ
3次関数の極値の差の公式を利用することで,具体的に極値を求めることなく,極値の差を求めることができる。
3次関数の極値の差3次関数 $C:f(x)=ax^3+bx^2+px+q$ が,$x=\alpha,~\beta~(\alpha<\beta)$ で極値をとるとすると,極値の差は次の式で求めることができる。
\begin{align*}
\abs{f(\alpha)-f(\beta)}=\dfrac{1}{2}\abs{a}(\beta-\alpha)^3
\end{align*}
\abs{f(\alpha)-f(\beta)}=\dfrac{1}{2}\abs{a}(\beta-\alpha)^3
\end{align*}

ヒロ
上の公式で絶対値記号を使っているのは,$x^3$ の係数が負の場合でも使えるようにするためである。

ヒロ
この公式を利用することで,計算が楽になるため,時間短縮につながる。また,検算にも利用できるため,使う人によっては,かなり効果が高くなるだろう。





















