Contents
2つの放物線の共通接線の交点を求める入試問題【大阪府立大】

ヒロ
次の問題を解いてみよう。
大阪府立大$f(x)=2x^2-4x+3,~$$g(x)=-x^2-2x-2$ とする。放物線 $y=f(x)$ と放物線 $y=g(x)$ の両方に接する2本の直線の交点の座標を求めよ。
微分を用いた解法

ヒロ
まずは,微分を用いた通常の解法で解いておこう。

ヒロ
具体的には $y=f(x)$ 上の点 $(t,~f(t))$ における接線が $y=g(x)$ と接する条件を考えよう。
$f(x)=2x^2-4x+3$ より
\begin{align*}
f'(x)=4x-4
\end{align*}
であるから,$y=f(x)$ 上の点 $(t,~f(t))$ における接線の方程式はf'(x)=4x-4
\end{align*}
\begin{align*}
y=(4t-4)x-2t^2+3~\cdots\cdots①
\end{align*}
この直線が $y=g(x)$ に接する条件はy=(4t-4)x-2t^2+3~\cdots\cdots①
\end{align*}
\begin{align*}
&-x^2-2x-2=(4t-4)x-2t^2+3 \\[4pt]
&x^2+(4t-2)x-2t^2+5=0~\cdots\cdots②
\end{align*}
が重解をもつことである。①の判別式を $D$ とすると,$D=0$ となるから&-x^2-2x-2=(4t-4)x-2t^2+3 \\[4pt]
&x^2+(4t-2)x-2t^2+5=0~\cdots\cdots②
\end{align*}
\begin{align*}
&(2t-1)^2-(-2t^2+5)=0 \\[4pt]
&6t^2-4t-4=0 \\[4pt]
&3t^2-2t-2=0~\cdots\cdots③ \\[4pt]
&t=\dfrac{1\pm\sqrt{7}}{3}
\end{align*}
&(2t-1)^2-(-2t^2+5)=0 \\[4pt]
&6t^2-4t-4=0 \\[4pt]
&3t^2-2t-2=0~\cdots\cdots③ \\[4pt]
&t=\dfrac{1\pm\sqrt{7}}{3}
\end{align*}

ヒロ
③を解いて $t$ の値を求めたけど,実際には③を解く必要はない。いま,求めなければならないのは,2本の接線の交点の座標だね。

ヒロ
2本の接線の方程式を求めれば,それらを連立することで確かに2接線の交点の座標を求めることはできる。③の解が簡単な整数解になるなら,それらを①に代入して2接線の方程式を求めて連立して解けば良いだろう。

ヒロ
しかし,今回の③の解を①に代入して接線の方程式を求めるのは面倒。
③の判別式を $D_1$ とすると
\begin{align*}
\dfrac{D_1}{4}=(-1)^2-3\Cdota(-2)=7>0
\end{align*}
\dfrac{D_1}{4}=(-1)^2-3\Cdota(-2)=7>0
\end{align*}

ヒロ
この計算で③が異なる2解をもつことは分かるから,その2解を文字で表して,必要なら最後に代入すれば良い。
③の2解を $\alpha,~\beta$ とおくと,解と係数の関係より
\begin{align*}
\alpha+\beta=\dfrac{2}{3},~\alpha\beta=-\dfrac{2}{3}
\end{align*}
①より,2本の接線の方程式は次のようになる。\alpha+\beta=\dfrac{2}{3},~\alpha\beta=-\dfrac{2}{3}
\end{align*}
\begin{align*}
&y=(4\alpha-4)x-2\alpha^2+3 \\[4pt]
&y=(4\beta-4)x-2\beta^2+3
\end{align*}
これらの辺々を引いて $y$ を消去すると&y=(4\alpha-4)x-2\alpha^2+3 \\[4pt]
&y=(4\beta-4)x-2\beta^2+3
\end{align*}
\begin{align*}
&4(\alpha-\beta)x-2(\alpha^2-\beta^2)=0 \\[4pt]
&2(\alpha-\beta)x-(\alpha-\beta)(\alpha+\beta)=0 \\[4pt]
&2(\alpha-\beta)\left(x-\dfrac{\alpha+\beta}{2}\right)=0
\end{align*}
$\alpha\neq\beta$ より&4(\alpha-\beta)x-2(\alpha^2-\beta^2)=0 \\[4pt]
&2(\alpha-\beta)x-(\alpha-\beta)(\alpha+\beta)=0 \\[4pt]
&2(\alpha-\beta)\left(x-\dfrac{\alpha+\beta}{2}\right)=0
\end{align*}
\begin{align*}
x=\dfrac{\alpha+\beta}{2}=\dfrac{1}{3}
\end{align*}
$y$ 座標はx=\dfrac{\alpha+\beta}{2}=\dfrac{1}{3}
\end{align*}
\begin{align*}
y&=(4\alpha-4)\Cdota\dfrac{\alpha+\beta}{2}-2\alpha^2+3 \\[4pt]
&=2\alpha\beta-2(\alpha+\beta)+3 \\[4pt]
&=2\Cdota\left(-\dfrac{2}{3}\right)-2\Cdota\dfrac{1}{3}+3 \\[4pt]
&=\dfrac{1}{3}
\end{align*}
よって,求める交点の座標は $\left(\dfrac{1}{3},~\dfrac{1}{3}\right)$y&=(4\alpha-4)\Cdota\dfrac{\alpha+\beta}{2}-2\alpha^2+3 \\[4pt]
&=2\alpha\beta-2(\alpha+\beta)+3 \\[4pt]
&=2\Cdota\left(-\dfrac{2}{3}\right)-2\Cdota\dfrac{1}{3}+3 \\[4pt]
&=\dfrac{1}{3}
\end{align*}
放物線の共通接線は相似の中心で交わる

ヒロ
幸か不幸か,君はこの記事をここまで読んでいる。ということは,2つの放物線の共通接線が相似の中心で交わることも既に知ってしまっている。
$f(x)=2x^2-4x+3,~$$g(x)=-x^2-2x-2$ とする。放物線 $y=f(x)$ と放物線 $y=g(x)$ の両方に接する2本の直線の交点の座標を求めよ。

ヒロ
知識があることによって,「この問題の2接線の交点は相似の中心である」ということが一瞬で分かってしまう。記述式であるかは関係なく,最初に君は2つの放物線の頂点から相似の中心をサラッと求めてしまうだろう。
$f(x)=2x^2-4x+3,~$$g(x)=-x^2-2x-2$ より
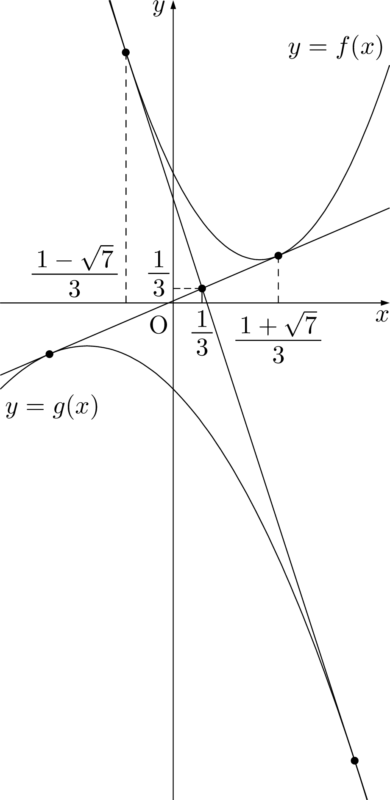
【参考図】そのまま図示すると縦に長くなりすぎるため,$y$ 軸方向に $\dfrac{1}{2}$ 倍している。
\begin{align*}
f(x)=2(x-1)^2+1,~g(x)=-(x+1)^2-1
\end{align*}
となるから,2つの放物線 $y=f(x),~$$y=g(x)$ の頂点をそれぞれP, Qとするとf(x)=2(x-1)^2+1,~g(x)=-(x+1)^2-1
\end{align*}
\begin{align*}
\mathrm{P}(1,~1),~\mathrm{Q}(-1,~-1)
\end{align*}
相似の中心をAとすると,点Aは2点P, Qを $1:2$ に内分する点であるから\mathrm{P}(1,~1),~\mathrm{Q}(-1,~-1)
\end{align*}
\begin{align*}
\dfrac{2\Cdot1+1\Cdot(-1)}{3}=\dfrac{1}{3}
\end{align*}
の計算により,$\mathrm{A}\left(\dfrac{1}{3},~\dfrac{1}{3}\right)$ となる。\dfrac{2\Cdot1+1\Cdot(-1)}{3}=\dfrac{1}{3}
\end{align*}
【参考図】そのまま図示すると縦に長くなりすぎるため,$y$ 軸方向に $\dfrac{1}{2}$ 倍している。



















