今回は絶対値を含む三角関数の最大最小問題について説明します。
具体的に,2019年に小樽商科大で出題された問題を2通りの解法で説明します。解法の違いによって,計算量は変わります。何でもかんでも「三角関数の合成」という考え方ではなく,問題に応じて解法を変えることができるようにすることが大切です。
2019年 小樽商科大$0\leqq\theta\leqq\pi$ のとき,関数 $y=2\sin\theta+\abs{2\cos\theta-1}$ の最大値 $M$ および 最小値 $m$ を求めると,$(M,~m)=\myhako$ である。
絶対値記号を外して合成する解法

ヒロ
絶対値記号があるとどうにもならないから,場合分けをして絶対値を外そう。
【場合分けのための計算】
$2\cos\theta-1\geqq0$ のとき,
\begin{align*}
&\cos\theta\geqq\dfrac{1}{2} \\[4pt]
&0\leqq\theta\leqq\dfrac{2\pi}{3}
\end{align*}
&\cos\theta\geqq\dfrac{1}{2} \\[4pt]
&0\leqq\theta\leqq\dfrac{2\pi}{3}
\end{align*}

ヒロ
その後は,$\sin\theta$ と $\cos\theta$ の1次式の和で表されているから,三角関数の合成で角をまとめよう。
$0\leqq\theta\leqq\dfrac{\pi}{3}$ のとき
グラフより,
\begin{align*}
y&=2\sin\theta+2\cos\theta-1 \\[4pt]
&=2\sqrt2\sin\left(\theta+\dfrac{\pi}{4}\right)-1
\end{align*}
$\dfrac{\pi}{3}\leqq\theta\leqq\pi$ のときy&=2\sin\theta+2\cos\theta-1 \\[4pt]
&=2\sqrt2\sin\left(\theta+\dfrac{\pi}{4}\right)-1
\end{align*}
\begin{align*}
y&=2\sin\theta-(2\cos\theta-1) \\[4pt]
&=2\sqrt2\sin\left(\theta-\dfrac{\pi}{4}\right)+1
\end{align*}
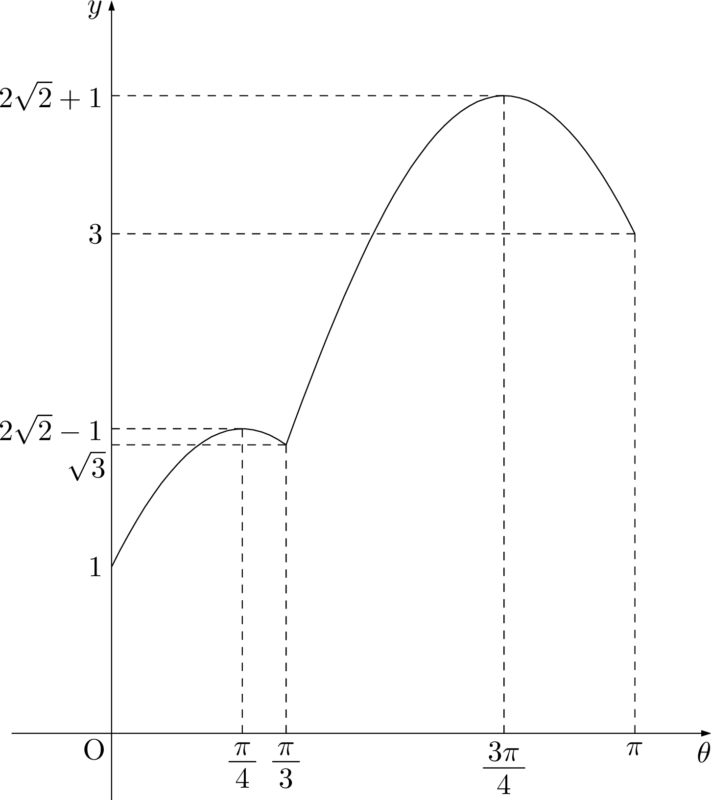
よって,$0\leqq\theta\leqq\pi$ におけるグラフは次のようになる。y&=2\sin\theta-(2\cos\theta-1) \\[4pt]
&=2\sqrt2\sin\left(\theta-\dfrac{\pi}{4}\right)+1
\end{align*}

グラフより,
\begin{align*}
M=2\sqrt{2}+1,~m=1
\end{align*}
M=2\sqrt{2}+1,~m=1
\end{align*}

ヒロ
グラフをサラッと描くことが出来れば簡単に解ける。しかし,このグラフを描くのに時間がかかる受験生は結構いるだろう。
単位円を利用する解法

ヒロ
点 $(\cos\theta,~\sin\theta)$ 原点を中心とする単位円周上の点であることを利用しよう。
$\cos\theta=X,~\sin\theta=Y$ とおくと,$0\leqq\theta\leqq\pi$ のとき
この折れ線を $(\ast)$ で表される半円と共有点をもつように動かして $y$ の最大値と最小値を求める。
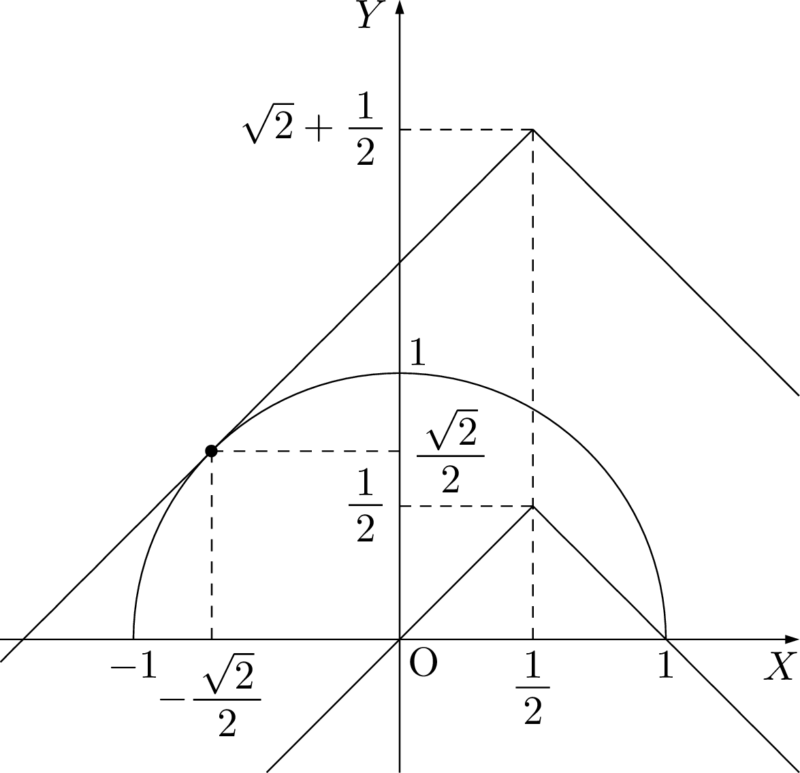
グラフより,折れ線が点 $\left(-\dfrac{\sqrt{2}}{2},~\dfrac{\sqrt{2}}{2}\right)$ を通るとき,$y$ は最大になるから,
\begin{align*}
\begin{cases}
X^2+Y^2=1 \\[4pt]
-1\leqq X\leqq1,~Y\geqq0
\end{cases}~\cdots\cdots(\ast)
\end{align*}
であり,$y$ は\begin{cases}
X^2+Y^2=1 \\[4pt]
-1\leqq X\leqq1,~Y\geqq0
\end{cases}~\cdots\cdots(\ast)
\end{align*}
\begin{align*}
y&=2\sin\theta+\abs{2\cos\theta-1} \\[4pt]
&=2Y+\abs{2X-1}
\end{align*}
となる。これよりy&=2\sin\theta+\abs{2\cos\theta-1} \\[4pt]
&=2Y+\abs{2X-1}
\end{align*}
\begin{align*}
&2Y+\abs{2X-1}=y \\[4pt]
&Y=-\abs{X-\dfrac{1}{2}}+\dfrac{y}{2}
\end{align*}
となり,$XY$ 平面上で折れ線を表す。&2Y+\abs{2X-1}=y \\[4pt]
&Y=-\abs{X-\dfrac{1}{2}}+\dfrac{y}{2}
\end{align*}
この折れ線を $(\ast)$ で表される半円と共有点をもつように動かして $y$ の最大値と最小値を求める。

グラフより,折れ線が点 $\left(-\dfrac{\sqrt{2}}{2},~\dfrac{\sqrt{2}}{2}\right)$ を通るとき,$y$ は最大になるから,
\begin{align*}
M&=2\Cdota\dfrac{\sqrt{2}}{2}+\abs{2\Cdota\left(-\dfrac{\sqrt{2}}{2}\right)-1} \\[4pt]
&=2\sqrt{2}+2
\end{align*}
また,点 $(1,~0)$ を通るとき,$y$ は最小になるからM&=2\Cdota\dfrac{\sqrt{2}}{2}+\abs{2\Cdota\left(-\dfrac{\sqrt{2}}{2}\right)-1} \\[4pt]
&=2\sqrt{2}+2
\end{align*}
\begin{align*}
m&=2\Cdota0+\abs{2\Cdota1-1} \\[4pt]
&=1
\end{align*}
m&=2\Cdota0+\abs{2\Cdota1-1} \\[4pt]
&=1
\end{align*}

ヒロ
最初の解法とは異なり,三角関数の合成も必要なく,折れ線を動かすだけなので,比較的楽に答えを求めることが出来る気がする。
まとめ

ヒロ
記述式でない問題に対しては,楽に速く答えを求めることができる解法は心強いものになる。

ヒロ
そのためには様々な考え方や知識が必要なので,日頃から複数の解法を知る努力をすることが大切。


















