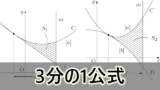
2つの放物線と共通接線で囲まれた部分の面積を求める方法を説明します。
一般的には「12分の1公式」と呼ばれる公式を利用することで,2つの放物線と共通接線で囲まれた部分の面積を簡単に求めることができます。
具体的な問題を通して,12分の1公式の使い方などを学びましょう。
Contents
12分の1公式

ヒロ
放物線と2本の接線で囲まれた部分の面積を求める公式が12分の1公式として知られているが,2つの放物線と共通接線で囲まれた部分の面積も12分の1公式で求めることができる。
12分の1公式2つの2次関数 $C:y=ax^2+\cdots,~D:y=ax^2+\cdots$ の共通接線を $l$ とし,接点の $x$ 座標を $\alpha,~\beta~(\alpha<\beta)$ とする。$C,~D,~l$ で囲まれた部分の面積を $S$ とすると,
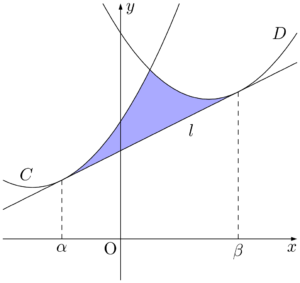
\begin{align*} S=\dfrac{1}{12}\abs{a}(\beta-\alpha)^3 \end{align*}
となる。

ヒロ
$x^2$ の係数が等しいときしか使えないため,注意が必要である。

ヒロ
$x^2$ の係数が異なるときは,2つの放物線の交点を通り $y$ 軸に平行な直線で2つに分割して,3分の1公式を利用しよう。
2020年 立命館大
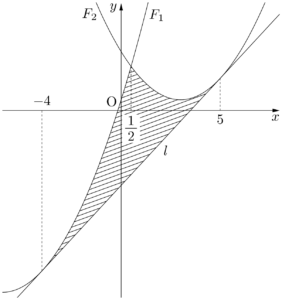
2020年 立命館大2つの放物線 $F_1:y=x^2+12x+2$ と $F_2:y=x^2-6x+11$ がある。$F_1$ と $F_2$ の両方に接する直線 $l$ は $y=\myhako\;x-\myhako$ である。このとき,放物線 $F_1$ と直線 $l$ は点 $\left(\myhako,~\myhako\right)$ で接しており,放物線 $F_2$ と直線 $l$ は点 $\left(\myhako,~\myhako\right)$ で接している。また,2つの放物線 $F_1,~F_2$ と直線 $l$ で囲まれた部分の面積は $\myhako$ である。

ヒロ
空欄を埋めることだけを考えた場合は,次のような解答になる。
【解答】
$F_1,~F_2$ の共通接線 $l$ の傾きは,2つの放物線の頂点を結んだ直線の傾きと等しい。
2つの放物線 $F_1,~F_2$ と直線 $l$ で囲まれた部分の面積は,12分の1公式より
$F_1,~F_2$ の共通接線 $l$ の傾きは,2つの放物線の頂点を結んだ直線の傾きと等しい。
\begin{align*}
&F_1:y=(x+6)^2-34 \\[4pt]&F_2:y=(x-3)^2+2
\end{align*}
2つの放物線の頂点の座標は $(-6,~-34),~(3,~2)$ となるから,$l$ の傾きは&F_1:y=(x+6)^2-34 \\[4pt]&F_2:y=(x-3)^2+2
\end{align*}
\begin{align*}
\dfrac{-34-2}{-6-3}=4
\end{align*}
$F_1:y=x^2+12x+2$ の導関数は\dfrac{-34-2}{-6-3}=4
\end{align*}
\begin{align*}
y’=2x+12
\end{align*}
となるから,$y’=4$ とするとy’=2x+12
\end{align*}
\begin{align*}
&2x+12=4 \\[4pt]&x=-4
\end{align*}
よって,$F_1$ と $l$ は $(-4,~-30)$ で接している。また,2つの放物線の頂点の $x$ 座標の差は9であるから,$F_2$ と $l$ は $(5,~6)$ で接している。また,$l$ の方程式は $y=4x-14$ である。&2x+12=4 \\[4pt]&x=-4
\end{align*}
2つの放物線 $F_1,~F_2$ と直線 $l$ で囲まれた部分の面積は,12分の1公式より
\begin{align*}
\dfrac{1}{12}\Cdota9^3=\dfrac{243}{4}
\end{align*}
\dfrac{1}{12}\Cdota9^3=\dfrac{243}{4}
\end{align*}

ヒロ
上の解法の詳細については,次の記事を参考にすると良いだろう。

ヒロ
特別な知識に頼らずに考えると,次のような解答になる。
【解答と考え方】
2つの曲線の共通接線の方程式を求めるときは,1つの曲線上の点における接線を考えて,その接線がもう1つの曲線に接する条件を考える方法が基本である。$F_1:y=x^2+12x+2$ より,$y’=2x+12$ であるから,$F_1$ 上の点 $(t,~t^2+12t+2)$ における接線の方程式は
$t=-4$ のとき,②の重解は $x=t+9=5$ であるから,$l$ と $F_2$ との接点は $(5,~6)$ である。
2つの放物線 $F_1,~F_2$ の交点を求める。
求める面積を $S$ とすると
2つの曲線の共通接線の方程式を求めるときは,1つの曲線上の点における接線を考えて,その接線がもう1つの曲線に接する条件を考える方法が基本である。$F_1:y=x^2+12x+2$ より,$y’=2x+12$ であるから,$F_1$ 上の点 $(t,~t^2+12t+2)$ における接線の方程式は
\begin{align*}
&y=(2t+12)(x-t)+t^2+12t+2 \\[4pt]&y=(2t+12)x-t^2+2~\cdots\cdots①
\end{align*}
これと $F_2:y=x^2-6x+11$ から $y$ を消去すると&y=(2t+12)(x-t)+t^2+12t+2 \\[4pt]&y=(2t+12)x-t^2+2~\cdots\cdots①
\end{align*}
\begin{align*}
&x^2-6x+11=(2t+12)x-t^2+2 \\[4pt]&x^2-(2t+18)x+t^2+9=0~\cdots②
\end{align*}
①と $F_2$ が接するとき,②は重解をもつから,②の判別式を $D$ とすると,$D=0$ となる。&x^2-6x+11=(2t+12)x-t^2+2 \\[4pt]&x^2-(2t+18)x+t^2+9=0~\cdots②
\end{align*}
\begin{align*}
&(t+9)^2-(t^2+9)=0 \\[4pt]&18t+72=0 \\[4pt]&t=-4
\end{align*}
よって,共通接線 $l$ の方程式は&(t+9)^2-(t^2+9)=0 \\[4pt]&18t+72=0 \\[4pt]&t=-4
\end{align*}
\begin{align*}
y=4x-14
\end{align*}
となる。$l$ と $F_1$ との接点は $(-4,~-30)$ である。y=4x-14
\end{align*}
$t=-4$ のとき,②の重解は $x=t+9=5$ であるから,$l$ と $F_2$ との接点は $(5,~6)$ である。
2つの放物線 $F_1,~F_2$ の交点を求める。
\begin{align*}
&x^2+12x+2=x^2-6x+11 \\[4pt]&18x=9 \\[4pt]&x=\dfrac{1}{2}
\end{align*}
よって,2つの放物線 $F_1,~F_2$ と直線 $l$ で囲まれた部分は図の斜線部部である。&x^2+12x+2=x^2-6x+11 \\[4pt]&18x=9 \\[4pt]&x=\dfrac{1}{2}
\end{align*}

求める面積を $S$ とすると
\begin{align*}
S&=\dint{-4}{\frac{1}{2}}\{x^2+12x+2-(4x-14)\}\;dx+\dint{\frac{1}{2}}{5}\{x^2-6x+11-(4x-14)\}\;dx \\[4pt]&=\dint{-4}{\frac{1}{2}}(x+4)^2\;dx+\dint{\frac{1}{2}}{5}(x-5)^2\;dx \\[4pt]&=\Tint{\dfrac{1}{3}(x+4)^3}{-4}{\frac{1}{2}}+\Tint{\dfrac{1}{3}(x-5)^2}{\frac{1}{2}}{5} \\[4pt]&=\dfrac{1}{3}\left(\dfrac{9}{2}\right)^3-\dfrac{1}{3}\left(-\dfrac{9}{2}\right)^3 \\[4pt]&=\dfrac{243}{4}
\end{align*}
S&=\dint{-4}{\frac{1}{2}}\{x^2+12x+2-(4x-14)\}\;dx+\dint{\frac{1}{2}}{5}\{x^2-6x+11-(4x-14)\}\;dx \\[4pt]&=\dint{-4}{\frac{1}{2}}(x+4)^2\;dx+\dint{\frac{1}{2}}{5}(x-5)^2\;dx \\[4pt]&=\Tint{\dfrac{1}{3}(x+4)^3}{-4}{\frac{1}{2}}+\Tint{\dfrac{1}{3}(x-5)^2}{\frac{1}{2}}{5} \\[4pt]&=\dfrac{1}{3}\left(\dfrac{9}{2}\right)^3-\dfrac{1}{3}\left(-\dfrac{9}{2}\right)^3 \\[4pt]&=\dfrac{243}{4}
\end{align*}