Contents
相似であることがすぐに分かる入試問題【2019年 京都産業大】

ヒロ
相似比と面積比に関連する問題もある。
2019年 京都産業大Oを原点とする $xy$ 平面上において,放物線 $y=-2x^2+8x-6$ を考える。この放物線と $x$ 軸との共有点の $x$ 座標は,$\myBox{ア}$ および $\myBox{イ}$ である。ただし,$\mybox{ア}<\mybox{イ}$ とする。
放物線 $y=-2x^2+8x-6$ の $\mybox{ア}\leqq x\leqq\mybox{イ}$ である部分を $C$ とする。 $C$ 上に点Pをとり,線分OPを $2:1$ に外分する点をQとする。Pの座標が $(a,~b)$ のとき,Qの座標は $\left(\myBox{ウエ},~\myBox{オカ}\right)$ である。Pが $C$ 上を動くとき,Qの軌跡 $C’$ は
Pが $C$ 上を動くとき,線分OPが通る部分の面積は $\myBox{ニ}\sqrt{\myBox{ヌ}}$ ,線分OQが通る部分の面積は $\myBox{ネ}\sqrt{\myBox{ノ}}$ である。
放物線 $y=-2x^2+8x-6$ の $\mybox{ア}\leqq x\leqq\mybox{イ}$ である部分を $C$ とする。 $C$ 上に点Pをとり,線分OPを $2:1$ に外分する点をQとする。Pの座標が $(a,~b)$ のとき,Qの座標は $\left(\myBox{ウエ},~\myBox{オカ}\right)$ である。Pが $C$ 上を動くとき,Qの軌跡 $C’$ は
\begin{align*}
y=\myBox{キ}\,x^2+\myBox{ク}\,x-\myBox{ケコ}~\left(\myBox{サ}\leqq x\leqq\myBox{シ}\right)
\end{align*}
と表される。$C$ と $C’$ の両方に接する直線 $l$ の方程式はy=\myBox{キ}\,x^2+\myBox{ク}\,x-\myBox{ケコ}~\left(\myBox{サ}\leqq x\leqq\myBox{シ}\right)
\end{align*}
\begin{align*}
\myBox{スセ}-\myBox{ソ}\sqrt{\myBox{タ}}\,\myBox{チ}-\myBox{ツ}=0
\end{align*}
であり,$l$ と $C$,$l$ と $C’$ の接点の $x$ 座標はそれぞれ $\sqrt{\myBox{テ}},~\myBox{ト}\sqrt{\myBox{ナ}}$ である。\myBox{スセ}-\myBox{ソ}\sqrt{\myBox{タ}}\,\myBox{チ}-\myBox{ツ}=0
\end{align*}
Pが $C$ 上を動くとき,線分OPが通る部分の面積は $\myBox{ニ}\sqrt{\myBox{ヌ}}$ ,線分OQが通る部分の面積は $\myBox{ネ}\sqrt{\myBox{ノ}}$ である。

ヒロ
サクサク解いていこう。
【アとイ】
$y=-2x^2+8x-6$ において $y=0$ として
$y=-2x^2+8x-6$ において $y=0$ として
\begin{align*}
&x^2-4x+3=0 \\[4pt]
&(x-1)(x-3)=0 \\[4pt]
&x=1,~3
\end{align*}
&x^2-4x+3=0 \\[4pt]
&(x-1)(x-3)=0 \\[4pt]
&x=1,~3
\end{align*}

ヒロ
問題文から原点が $C$ と $C’$ の相似の中心であることが分かる。また,$C$ 上の点が原点との距離が2倍になる点に移されることと $x^2$ の係数は $\dfrac{1}{2}$ 倍になることが分かる。
【ウからシまで】
Pの座標が $(a,~b)$ のとき,Qの座標は $(2a,~2b)$ となる。よって,$C$ の2つの端点 $(1,~0)$, $(3,~0)$ はそれぞれ $(2,~0)$, $(6,~0)$ に移される。
また,$C:y=-2(x-2)^2+2$ より $C$ の頂点の座標は $(2,~2)$ であるから,$C’$ の頂点の座標は $(4,~4)$ となる。よって,$C’$ は
Pの座標が $(a,~b)$ のとき,Qの座標は $(2a,~2b)$ となる。よって,$C$ の2つの端点 $(1,~0)$, $(3,~0)$ はそれぞれ $(2,~0)$, $(6,~0)$ に移される。
また,$C:y=-2(x-2)^2+2$ より $C$ の頂点の座標は $(2,~2)$ であるから,$C’$ の頂点の座標は $(4,~4)$ となる。よって,$C’$ は
\begin{align*}
&y=-(x-4)^2+4~(2\leqq x\leqq6)\\
&y=-x^2+8x-12~(2\leqq x\leqq6)
\end{align*}
&y=-(x-4)^2+4~(2\leqq x\leqq6)\\
&y=-x^2+8x-12~(2\leqq x\leqq6)
\end{align*}

ヒロ
2乗に比例する性質を利用して接線の方程式を求めよう。
【スからナまで】
$C$ と $C’$ の共通接線は相似の中心である原点を通る。
$C$ の $x^2$ の係数が $-2$ だから,$l$ と $C$ の接点の $x$ 座標を $t$ とすると
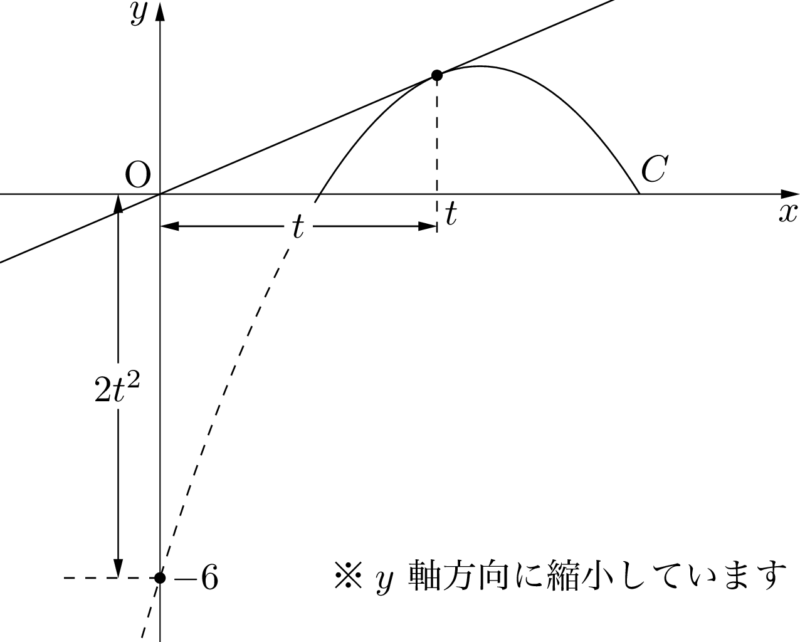
接点の $y$ 座標は
$C$ と $C’$ の共通接線は相似の中心である原点を通る。
$C$ の $x^2$ の係数が $-2$ だから,$l$ と $C$ の接点の $x$ 座標を $t$ とすると
\begin{align*}
2t^2=6
\end{align*}
が成り立つ。$t>0$ より,$t=\sqrt{3}$ となる。2t^2=6
\end{align*}

接点の $y$ 座標は
\begin{align*}
-2(\sqrt{3})^2+8\sqrt{3}-6=-12+8\sqrt{3}
\end{align*}
であるから,共通接線 $l$ の方程式は-2(\sqrt{3})^2+8\sqrt{3}-6=-12+8\sqrt{3}
\end{align*}
\begin{align*}
&y=\dfrac{-12+8\sqrt{3}}{\sqrt{3}}x \\[4pt]
&y=(-4\sqrt{3}+8)x \\[4pt]
&8x-4\sqrt{3}x-y=0
\end{align*}
$C$ と $l$ の接点の $x$ 座標が $\sqrt{3}$ であるから,$C’$ と $l$ の接点の $x$ 座標は $2\sqrt{3}$ となる。&y=\dfrac{-12+8\sqrt{3}}{\sqrt{3}}x \\[4pt]
&y=(-4\sqrt{3}+8)x \\[4pt]
&8x-4\sqrt{3}x-y=0
\end{align*}

ヒロ
最後は面積を求める問題。計算量を少なくなるように,うまく求めよう。
【ニとヌ】
線分OPが通る部分は図の斜線部分となる。
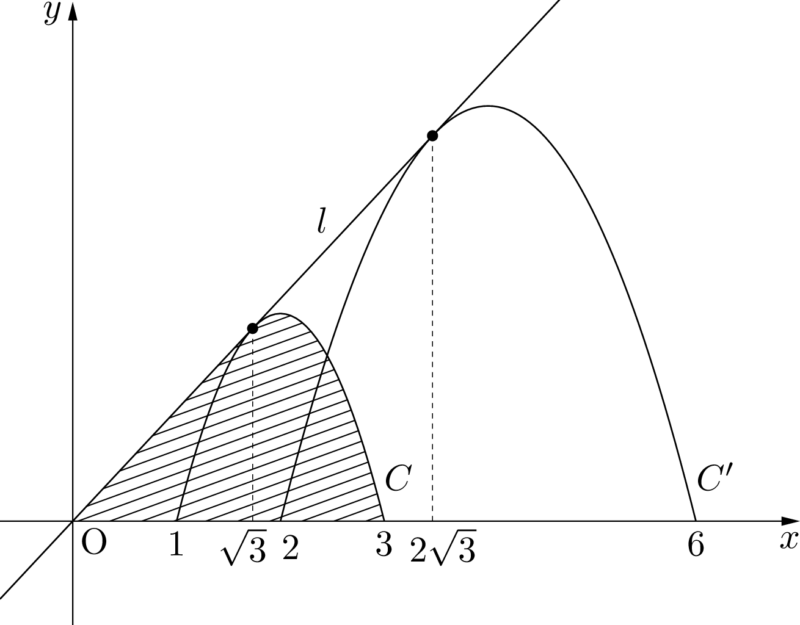
補助線を引くことで斜線部分を三角形と6分の1公式を使える部分に分割することができる。
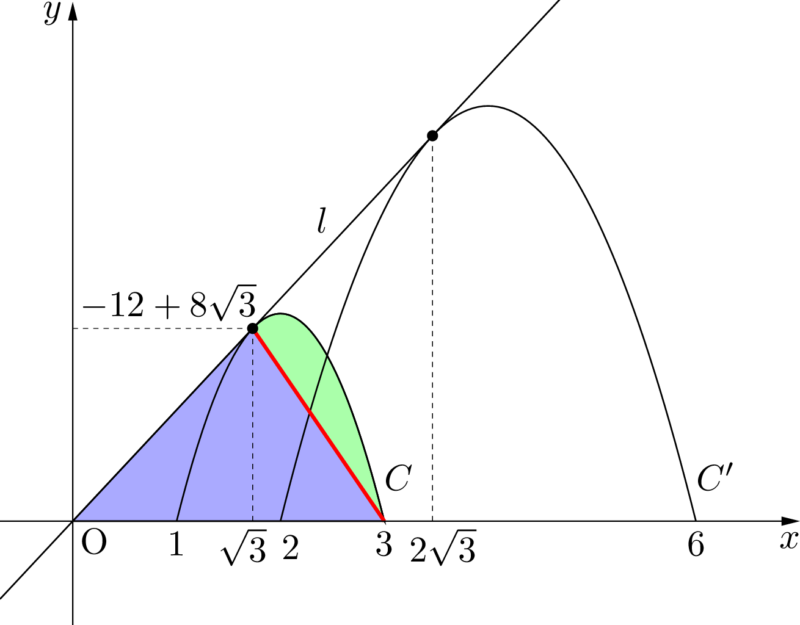
斜線部分の面積を $S_1$ とすると
線分OPが通る部分は図の斜線部分となる。

補助線を引くことで斜線部分を三角形と6分の1公式を使える部分に分割することができる。

斜線部分の面積を $S_1$ とすると
\begin{align*}
S_1&=\dfrac{1}{2}\Cdota3\Cdota(-12+8\sqrt{3})+\dfrac{1}{6}\Cdota2(3-\sqrt{3})^3 \\[4pt]
&=3(-6+4\sqrt{3})+\dfrac{1}{3}(27-27\sqrt{3}+27-3\sqrt{3}) \\[4pt]
&=2\sqrt{3}
\end{align*}
S_1&=\dfrac{1}{2}\Cdota3\Cdota(-12+8\sqrt{3})+\dfrac{1}{6}\Cdota2(3-\sqrt{3})^3 \\[4pt]
&=3(-6+4\sqrt{3})+\dfrac{1}{3}(27-27\sqrt{3}+27-3\sqrt{3}) \\[4pt]
&=2\sqrt{3}
\end{align*}

ヒロ
最後は相似比と面積比の関係を利用しよう。
【ネとノ】
線分OQが通る部分は図の斜線部分となる。
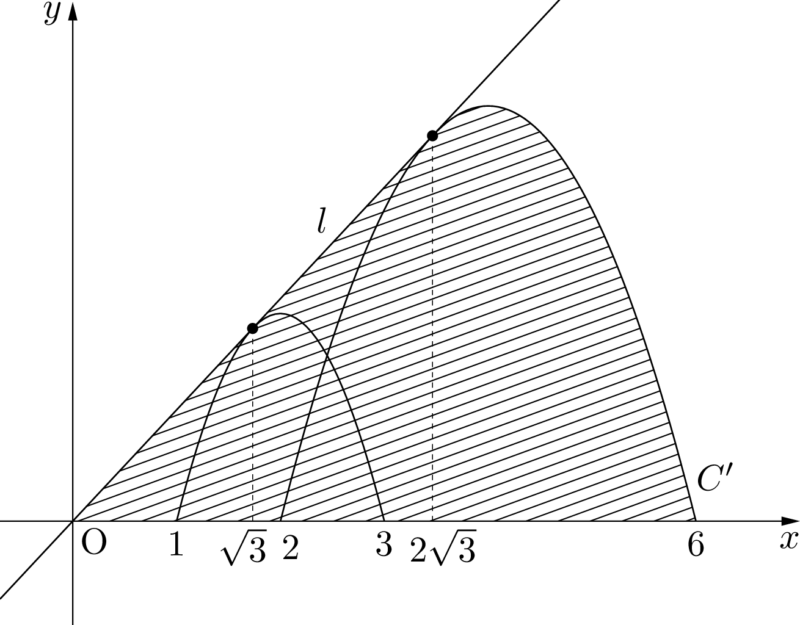
斜線部分は線分OPが通過する部分と相似であり,相似比は $1:2$ であるから,面積比は $1:4$ である。斜線部分の面積を $S_2$ とすると
線分OQが通る部分は図の斜線部分となる。

斜線部分は線分OPが通過する部分と相似であり,相似比は $1:2$ であるから,面積比は $1:4$ である。斜線部分の面積を $S_2$ とすると
\begin{align*}
S_2=4S_1=8\sqrt{3}
\end{align*}
S_2=4S_1=8\sqrt{3}
\end{align*}
まとめ

ヒロ
2つの放物線の共通接線を求める問題では,放物線に関する知識を利用することで,簡単に求めることができる。

ヒロ
マーク式試験のような答えだけを求めれば良い問題に対しては,特に有効である。

ヒロ
また,記述を始める前に簡単な計算で答えが分かっているから,もし途中で間違えた場合は,間違えたことにすぐに気付けるというメリットがある。

ヒロ
しかし,記述試験においては,答えだけはすぐに分かるが,しっかりと書かないと点数を貰えないから面倒に感じる点がデメリットになるだろう。



















