Contents
2つの放物線の共通接線を求める問題【オリジナル問題】
オリジナル問題$f(x)=2x^2-8x+17$, $g(x)=-x^2-2x-10$ とする。放物線 $C_1:y=f(x)$ と放物線 $C_2:y=g(x)$ の両方に接する2本の直線の方程式は,$y=\myhako$, $y=\myhako$ である。

ヒロ
まずは2本の共通接線の交点である相似の中心を求めよう。
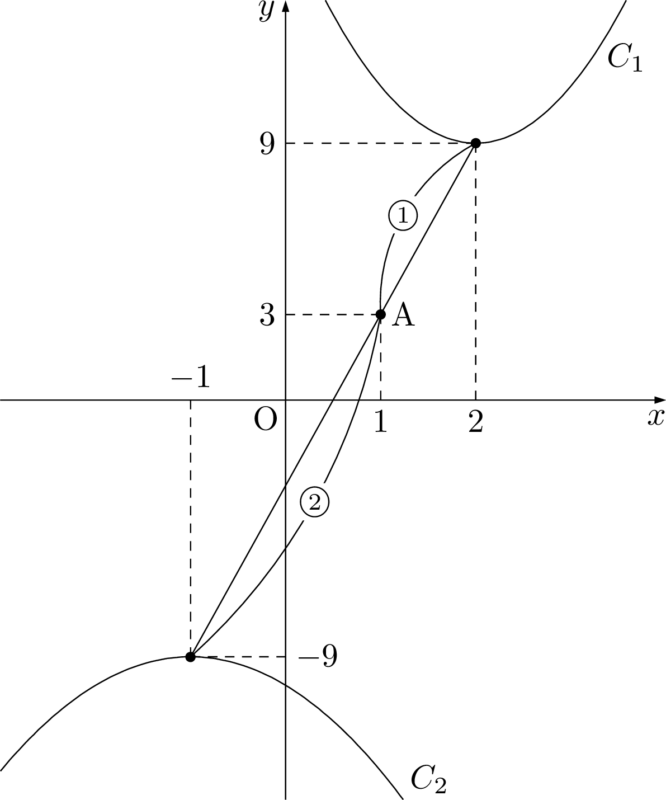
$f(x)=2(x-2)^2+9$, $g(x)=-(x+1)^2-9$ より,$C_1,~C_2$ の頂点の座標はそれぞれ次のようになる。
\begin{align*}
(2,~9),~(-1,~-9)
\end{align*}
2つの放物線の相似の中心を $\mathrm{A}(x,~y)$ とすると,$C_1,~C_2$ の $x^2$ の係数より,(2,~9),~(-1,~-9)
\end{align*}
\begin{align*}
&x=\dfrac{1\Cdot(-1)+2\Cdot2}{3}=1 \\[4pt]
&y=\dfrac{1\Cdot(-9)+2\Cdot9}{3}=3
\end{align*}
よって,$C_1,~C_2$ の共通接線は点 $\mathrm{A}(1,~3)$ を通る。&x=\dfrac{1\Cdot(-1)+2\Cdot2}{3}=1 \\[4pt]
&y=\dfrac{1\Cdot(-9)+2\Cdot9}{3}=3
\end{align*}


ヒロ
通る点さえ求めてしまえば,あとは簡単だね。

ヒロ
点Aを通る直線が $C_1$ に接するとき,$C_2$ にも接するから,両方の放物線を気にする必要なない。
【$C_1$ との接点の $x$ 座標を求める】
$C_1$ 上の点 $\mathrm{P}(1,~f(1))$ を考えると,

$C_1$ 上の接点の $x$ 座標を $1\pm d~(d>0)$ とすると
$C_1$ 上の点 $\mathrm{P}(1,~f(1))$ を考えると,
\begin{align*}
\mathrm{AP}=(2-8+17)-3=8
\end{align*}
となる。\mathrm{AP}=(2-8+17)-3=8
\end{align*}

$C_1$ 上の接点の $x$ 座標を $1\pm d~(d>0)$ とすると
\begin{align*}
2d^2=8
\end{align*}
が成り立つ。これを解くと $d=2$ となるから,$C_1$ 上の接点の座標は次のようになる。2d^2=8
\end{align*}
\begin{align*}
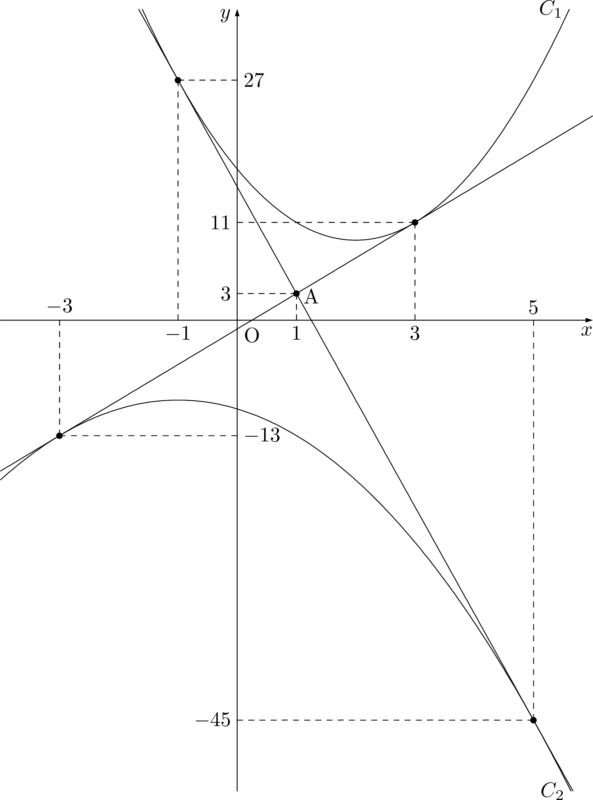
(3,~11),~(-1,~27)
\end{align*}
よって,求める2接線の方程式は次のようになる。(3,~11),~(-1,~27)
\end{align*}
\begin{align*}
y=4x-1,~y=-12x+15
\end{align*}
y=4x-1,~y=-12x+15
\end{align*}

ヒロ
$C_2$ との関係を考えた場合は,次のようにして接点の座標を求めることができる。
【$C_2$ との接点の $x$ 座標を求める】
$C_2$ 上の点 $\mathrm{Q}(1,~g(1))$ を考えると,
$C_2$ 上の点 $\mathrm{Q}(1,~g(1))$ を考えると,
\begin{align*}
\mathrm{AQ}=3-(-1-2-10)=16
\end{align*}
となる。$C_2$ 上の接点の $x$ 座標を $1\pm d~(d>0)$ とすると\mathrm{AQ}=3-(-1-2-10)=16
\end{align*}
\begin{align*}
d^2=16
\end{align*}
が成り立つ。これを解くと $d=4$ となるから,$C_2$ 上の接点の座標は次のようになる。d^2=16
\end{align*}
\begin{align*}
(5,~-45),~(-3,~-13)
\end{align*}
(5,~-45),~(-3,~-13)
\end{align*}



















