Contents
【解法2】図形の性質を利用する

ヒロ
次は図形の性質を利用して考えよう。
2つの円 $C_1:x^2+y^2=25$,$C_2:(x-10)^2+y^2=100$ を考える。円 $C_1,~C_2$ の両方に接する直線の方程式を求めよ。
2つの円 $C_1,~C_2$ の共通接線は,次の図のように2本ある。2つの円はともに $x$ 軸に関して対称であるから,その共通接線も $x$ 軸に関して対称である。
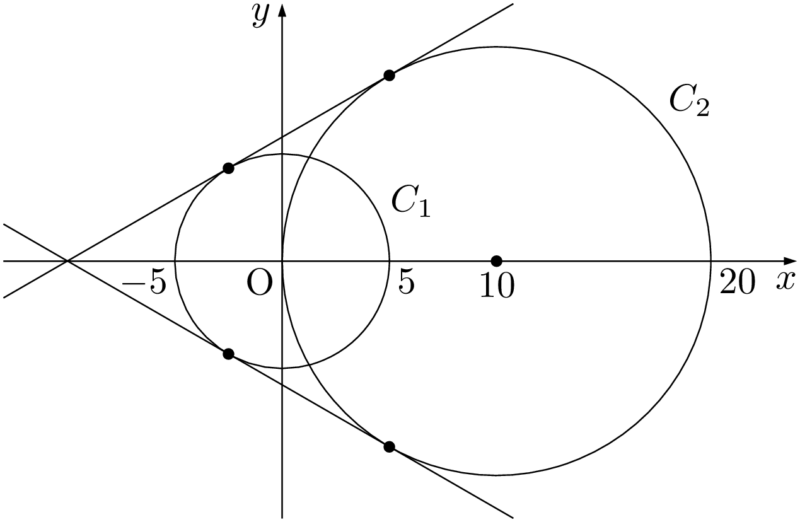
2本ある共通接線のうち,傾きが正であるものを $l$ とし,傾きが負であるものを $m$ とする。2つの円 $C_1,~C_2$ から接線 $l$ に下ろした垂線の足をそれぞれP,Qとし,2接線 $l,~m$ の交点をTとする。
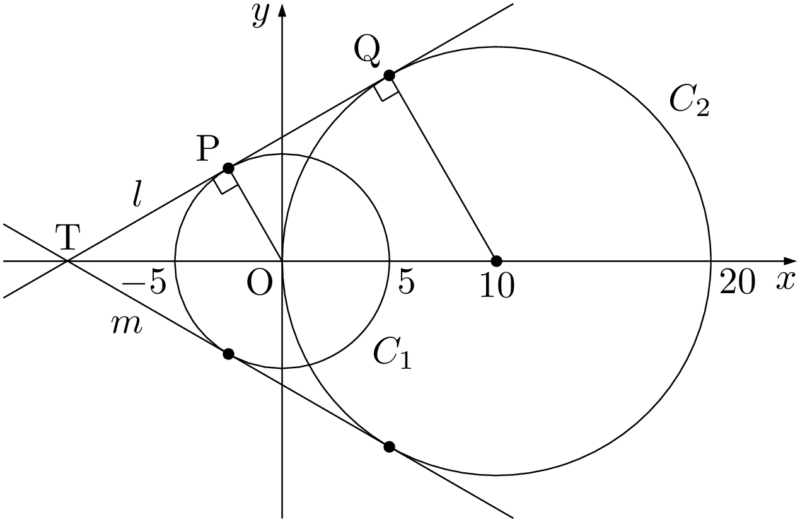
円 $C_2$ の中心をCとすると,$\sankaku{TOP}$ と $\sankaku{TCQ}$ は相似であることが分かる。
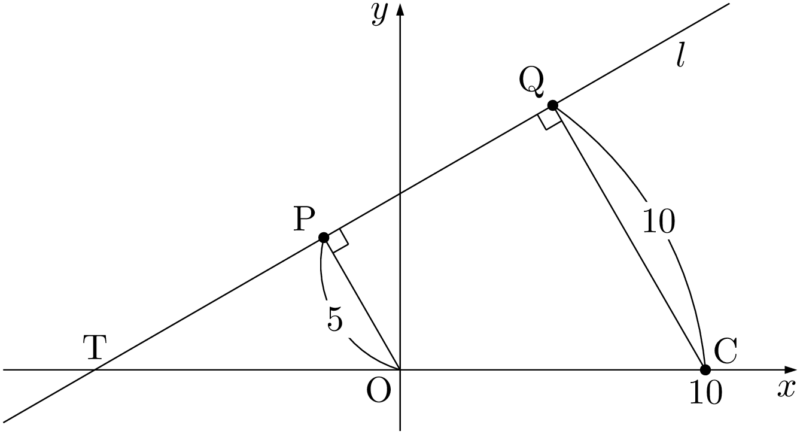
対応する辺の長さの比を考えると
このとき,三平方の定理より
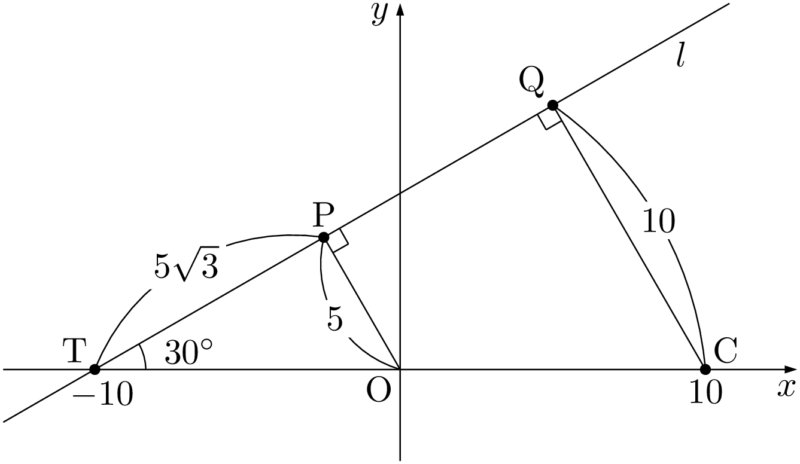
したがって,接線 $l$ の傾きは
接線 $m$ は $x$ 軸に関して $l$ と対称であるから,求める接線の方程式は

2本ある共通接線のうち,傾きが正であるものを $l$ とし,傾きが負であるものを $m$ とする。2つの円 $C_1,~C_2$ から接線 $l$ に下ろした垂線の足をそれぞれP,Qとし,2接線 $l,~m$ の交点をTとする。

円 $C_2$ の中心をCとすると,$\sankaku{TOP}$ と $\sankaku{TCQ}$ は相似であることが分かる。

対応する辺の長さの比を考えると
\begin{align*}
\text{OP}:\text{CQ}=5:10=1:2
\end{align*}
であるから,\text{OP}:\text{CQ}=5:10=1:2
\end{align*}
\begin{align*}
\text{TO}:\text{TC}=1:2
\end{align*}
となる。原点はOTの中点であるから,T$(-10,~0)$ と分かる。\text{TO}:\text{TC}=1:2
\end{align*}
このとき,三平方の定理より
\begin{align*}
\text{TP}=\sqrt{10^2-5^2}=5\sqrt{3}
\end{align*}
となるから,$\sankaku{TOP}$ は3辺の長さの比が $1:2:\sqrt{3}$ の直角三角形であることが分かる。\text{TP}=\sqrt{10^2-5^2}=5\sqrt{3}
\end{align*}

したがって,接線 $l$ の傾きは
\begin{align*}
\tan30\Deg=\dfrac{1}{\sqrt{3}}
\end{align*}
であるから,その方程式は $y=\dfrac{1}{\sqrt{3}}(x+10)$ である。\tan30\Deg=\dfrac{1}{\sqrt{3}}
\end{align*}
接線 $m$ は $x$ 軸に関して $l$ と対称であるから,求める接線の方程式は
\begin{align*}
y=\pm\dfrac{1}{\sqrt{3}}(x+10)
\end{align*}
y=\pm\dfrac{1}{\sqrt{3}}(x+10)
\end{align*}


















