Contents
【解法3】共通接線が通る定点を最初に求める

ヒロ
次のことを知っておくと良いだろう。
共通接線が通る定点2つの円 $C_1,~C_2$ の中心をそれぞれC,Dとし,半径をそれぞれ $r_1,~r_2$ とする。
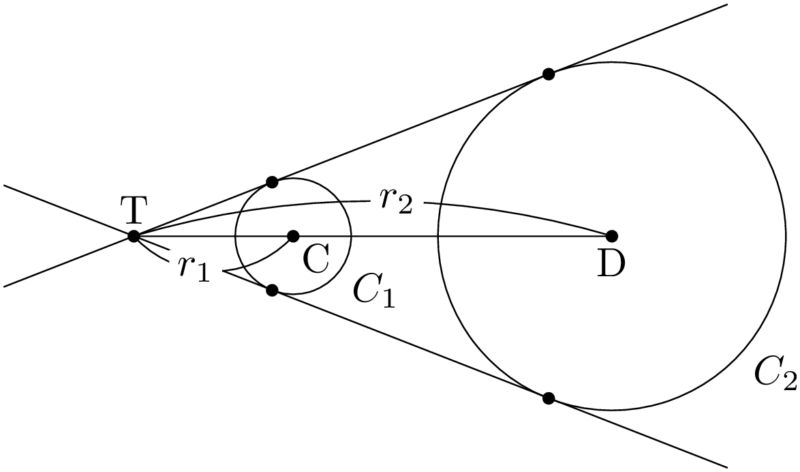
2つの円の共通外接線は線分CDを $r_1:r_2$ に外分する点Tを通る。
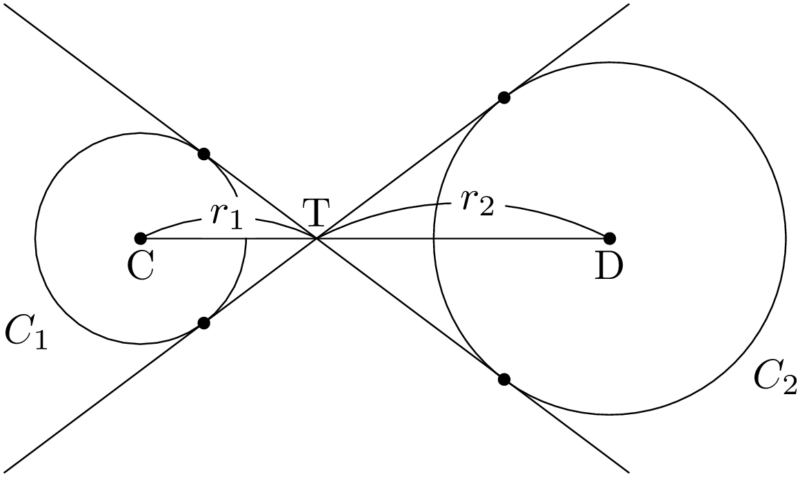
2つの円の共通内接線は線分CDを $r_1:r_2$ に内分する点Tを通る。
2つの円の共通外接線は線分CDを $r_1:r_2$ に外分する点Tを通る。

2つの円の共通内接線は線分CDを $r_1:r_2$ に内分する点Tを通る。


ヒロ
上のことを利用することで,簡単に通る点を求められるため,あとは傾きを求めれば良い。
2つの円 $C_1:x^2+y^2=25$,$C_2:(x-10)^2+y^2=100$ を考える。円 $C_1,~C_2$ の両方に接する直線の方程式を求めよ。
今回の問題では,共通外接線が2本存在することを最初に確かめた。2つの円 $C_1,~C_2$ の中心はそれぞれO$(0,~0)$,C$(10,~0)$ であり,半径はそれぞれ5,10である。OCを $1:2$ に外分する点を $(X,~Y)$ とすると
\begin{align*}
&X=\dfrac{-1\Cdot10+2\Cdot0}{-1+2}=-10 \\[4pt]
&Y=0
\end{align*}
よって,求める接線は点 $(-10,~0)$ を通る直線で,$y$ 軸と平行ではないから&X=\dfrac{-1\Cdot10+2\Cdot0}{-1+2}=-10 \\[4pt]
&Y=0
\end{align*}
\begin{align*}
&y=m(x+10) \\[4pt]
&mx-y+10m=0
\end{align*}
と表せる。この直線が $C_1$ と接するのは,原点との距離が5のときであるから&y=m(x+10) \\[4pt]
&mx-y+10m=0
\end{align*}
\begin{align*}
&\dfrac{\abs{10m}}{\sqrt{m^2+1}}=5 \\[4pt]
&\abs{2m}=\sqrt{m^2+1}
\end{align*}
両辺を2乗すると&\dfrac{\abs{10m}}{\sqrt{m^2+1}}=5 \\[4pt]
&\abs{2m}=\sqrt{m^2+1}
\end{align*}
\begin{align*}
&4m^2=m^2+1 \\[4pt]
&m^2=\dfrac{1}{3} \\[4pt]
&m=\pm\dfrac{1}{\sqrt{3}}
\end{align*}
したがって,求める接線の方程式は,$y=\pm\dfrac{1}{\sqrt{3}}(x+10)$&4m^2=m^2+1 \\[4pt]
&m^2=\dfrac{1}{3} \\[4pt]
&m=\pm\dfrac{1}{\sqrt{3}}
\end{align*}

ヒロ
求めた定点を通る直線が一方の円と接するとき,もう一方の円と必ず接するため,片方の円と接するときを考えれば良い。

ヒロ
そのため,共通接線が通るべき定点を最初に求めることで,少し楽に感じるかもしれない。


















