Contents
2つの円の共通接線を求める問題【岐阜聖徳大】
2018年 岐阜聖徳大2つの円 $C_1:x^2+y^2=25$,$C_2:(x-10)^2+y^2=100$ を考える。円 $C_1,~C_2$ の両方に接する直線の方程式を求めよ。

ヒロ
まず,2つの円の位置関係を調べることにする。
【2円の位置関係】
$C_1$ は中心が原点で半径5の円である。$C_2$ は中心が $(10,~0)$ で半径10の円である。中心間の距離を $d$ とすると,$d=10$ であるから
$C_1$ は中心が原点で半径5の円である。$C_2$ は中心が $(10,~0)$ で半径10の円である。中心間の距離を $d$ とすると,$d=10$ であるから
\begin{align*}
(半径の差)<d<(半径の和) \end{align*}
が成り立つ。よって,2つの円は2点で交わる。 2つの円の位置関係が分かったことによって,共通接線は2本存在することが分かる。 上で書いた5つの方法で,共通接線を求めることにする。(半径の差)<d<(半径の和) \end{align*}
【解法1】一方の円周上の点における接線が他方の円に接するときを考える

ヒロ
円周上の点における接線の公式を忘れている場合は,次の記事から確認しよう。

ヒロ
また,直線と円が接するときの考え方は,次の記事を参考にしよう。
$C_1$ 上の点 $(p,~q)$ における接線の方程式は
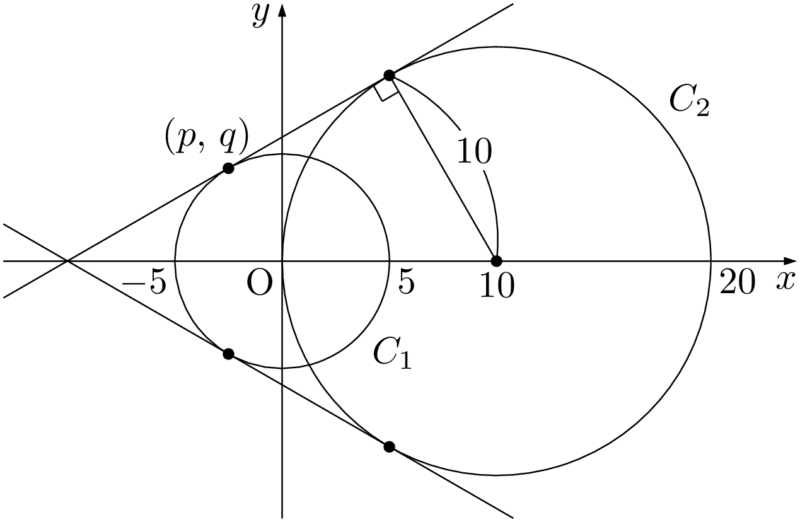
直線①が $C_2$ と接するとき,直線①と点 $(10,~0)$ との距離が10であるから
このとき②より
\begin{align*}
px+qy=25~\cdots\cdots①
\end{align*}
である。ただし,$p^2+q^2=25~\cdots\cdots②$ とする。px+qy=25~\cdots\cdots①
\end{align*}

直線①が $C_2$ と接するとき,直線①と点 $(10,~0)$ との距離が10であるから
\begin{align*}
&\dfrac{\abs{10p-25}}{\sqrt{p^2+q^2}}=10 \\[4pt]
&\abs{2p-5}=10~~(\because ②) \\[4pt]
&2p-5=\pm10 \\[4pt]
&p=\dfrac{15}{2},~-\dfrac{5}{2}
\end{align*}
②より,$-5\leqq p\leqq5$ であるから,$p=-\dfrac{5}{2}$&\dfrac{\abs{10p-25}}{\sqrt{p^2+q^2}}=10 \\[4pt]
&\abs{2p-5}=10~~(\because ②) \\[4pt]
&2p-5=\pm10 \\[4pt]
&p=\dfrac{15}{2},~-\dfrac{5}{2}
\end{align*}
このとき②より
\begin{align*}
&q^2=25-\dfrac{25}{4}=\dfrac{75}{4} \\[4pt]
&q=\pm\dfrac{5\sqrt{3}}{2}
\end{align*}
①より,求める接線の方程式は&q^2=25-\dfrac{25}{4}=\dfrac{75}{4} \\[4pt]
&q=\pm\dfrac{5\sqrt{3}}{2}
\end{align*}
\begin{align*}
&-\dfrac{5}{2}x\pm\dfrac{5\sqrt{3}}{2}y=25 \\[4pt]
&-x\pm\sqrt{3}y=10 \\[4pt]
&x\pm\sqrt{3}y+10=0
\end{align*}
&-\dfrac{5}{2}x\pm\dfrac{5\sqrt{3}}{2}y=25 \\[4pt]
&-x\pm\sqrt{3}y=10 \\[4pt]
&x\pm\sqrt{3}y+10=0
\end{align*}

ヒロ
直線③と円 $C_2$ が接するときを考えるときに,上の解答では,点と直線の距離を利用したが,2次方程式の判別式を利用する方法もある。

ヒロ
具体的には次のようになる。
$C_1$ 上の点 $(p,~q)$ における接線の方程式は
①を $C_2$ の方程式に代入すると
\begin{align*}
px+qy=25
\end{align*}
である。ここで,求める接線は $y$ 軸と平行ではないから $q\neq0$ であり,px+qy=25
\end{align*}
\begin{align*}
y=\dfrac{25-px}{q}~\cdots\cdots①
\end{align*}
と変形できる。ただし,$p^2+q^2=25~\cdots\cdots②$ とする。y=\dfrac{25-px}{q}~\cdots\cdots①
\end{align*}
①を $C_2$ の方程式に代入すると
\begin{align*}
&(x-10)^2+\left(\dfrac{25-px}{q}\right)^2=100 \\[4pt]
&q^2(x^2-20x+100)+(p^2x^2-50px+625)=100q^2 \\[4pt]
&(p^2+q^2)x^2+(-50p-20q^2)x+625=0 \\[4pt]
&25x^2-5(10p+4q^2)x+625=0~~(\because ②) \\[4pt]
&5x^2-2(5p+2q^2)+125=0~\cdots\cdots④
\end{align*}
直線①と円 $C_2$ が接するのは,2次方程式④が重解をもつときである。判別式を $D$ とすると&(x-10)^2+\left(\dfrac{25-px}{q}\right)^2=100 \\[4pt]
&q^2(x^2-20x+100)+(p^2x^2-50px+625)=100q^2 \\[4pt]
&(p^2+q^2)x^2+(-50p-20q^2)x+625=0 \\[4pt]
&25x^2-5(10p+4q^2)x+625=0~~(\because ②) \\[4pt]
&5x^2-2(5p+2q^2)+125=0~\cdots\cdots④
\end{align*}
\begin{align*}
&D/4=(5p+2q^2)^2-625=0 \\[4pt]
&5p+2q^2=\pm25 \\[4pt]
&5p+2(25-p^2)=\pm25 \\[4pt]
&2p^2-5p-25=0~~または~~2p^2-5p-75=0
\end{align*}
$2p^2-5p-25=0$ を解くと&D/4=(5p+2q^2)^2-625=0 \\[4pt]
&5p+2q^2=\pm25 \\[4pt]
&5p+2(25-p^2)=\pm25 \\[4pt]
&2p^2-5p-25=0~~または~~2p^2-5p-75=0
\end{align*}
\begin{align*}
&(p-5)(2p+5)=0 \\[4pt]
&p=5,~-\dfrac{5}{2}
\end{align*}
$2p^2-5p-75=0$ を解くと&(p-5)(2p+5)=0 \\[4pt]
&p=5,~-\dfrac{5}{2}
\end{align*}
\begin{align*}
&(p+5)(2p-15)=0 \\[4pt]
&p=-5,~\dfrac{15}{2}
\end{align*}
$q\neq0$ であるから,$q^2>0$ であり,②より
&(p+5)(2p-15)=0 \\[4pt]
&p=-5,~\dfrac{15}{2}
\end{align*}
\begin{align*} &25-p^2>0 \\[4pt] &-5<p<5 \end{align*}
これを満たす $p$ は,$p=-\dfrac{5}{2}$このとき,②より,$q=\pm\dfrac{5\sqrt{3}}{2}$
以上より,求める接線の方程式は
\begin{align*} x\pm\sqrt{3}y+10=0 \end{align*}

ヒロ
直線と円が接する条件を判別式を利用して考えると面倒である。




















