ここでは円に内接する四角形の面積について説明します。
大学入試問題では,円に内接する四角形に関する問題がよく出題されます。
円に内接する四角形の性質とよくある問題の流れを知っておきましょう。
円に内接する四角形の性質

ヒロ
「四角形が円に内接する」とはどういうことかを知っておこう。
円に内接する多角形一般に,多角形のすべての頂点が1つの円周上にあるとき,その多角形は円に内接するといい,その円を多角形の外接円という。


ヒロ
「すべての頂点が1つの円周上にある」という条件を忘れないようにしよう。

ヒロ
三角形の場合は,どのような三角形であっても,必ず円に内接するが,三角形以外の多角形は必ずしも円に内接するとは限らない。

ヒロ
ここでは,円に内接する四角形の性質について考えてみよう。
【円に内接する四角形】
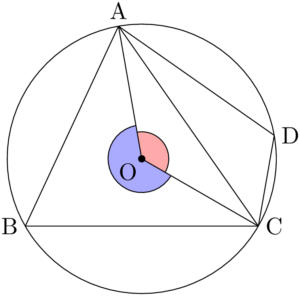
次のように,円に内接する四角形ABCDを考える。
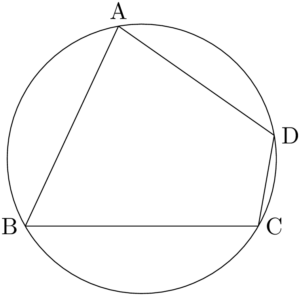
2点A, Cを結んで2つの三角形に分割する。
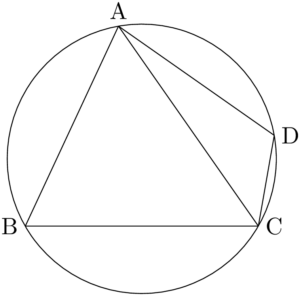
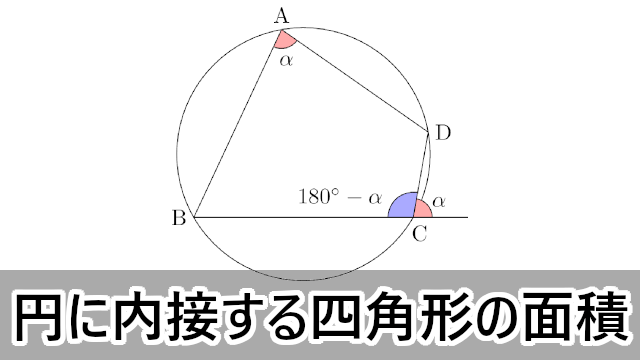
外接円の中心をOとして,円周角と中心角を考える。ピンクと青で塗った中心角の和は $360\Deg$ である。
同じ弧に対する円周角は中心角の半分であるから,ピンクと青で塗った円周角の和は $360\Deg$ の半分の $180\Deg$ である。
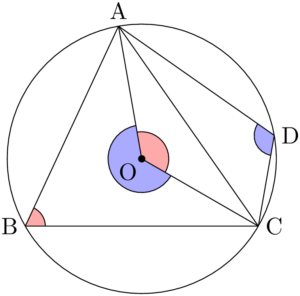
したがって,円に内接する四角形の対角の和は $180\Deg$ である。
また,このことから円に内接する四角形の内角は,その対角の外角に等しいことも分かる。
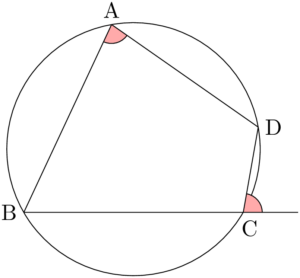
次のように,円に内接する四角形ABCDを考える。

2点A, Cを結んで2つの三角形に分割する。

外接円の中心をOとして,円周角と中心角を考える。ピンクと青で塗った中心角の和は $360\Deg$ である。

同じ弧に対する円周角は中心角の半分であるから,ピンクと青で塗った円周角の和は $360\Deg$ の半分の $180\Deg$ である。

したがって,円に内接する四角形の対角の和は $180\Deg$ である。
また,このことから円に内接する四角形の内角は,その対角の外角に等しいことも分かる。

円に内接する四角形
四角形が円に内接するとき,次の性質が成り立つ。
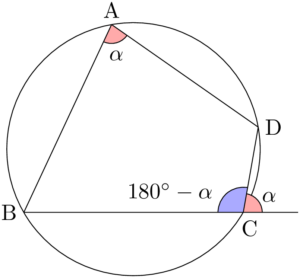

- 四角形の対角の和は $180\Deg$ である。
- 四角形の内角は,その対角の外角に等しい。
円に内接する四角形に関する問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題円に内接する四角形ABCDにおいて $\text{AB}=7$, $\text{BC}=8$, $\text{CD}=15$, $\text{DA}=7$ である。以下の問いに答えよ。
(1) $\cos B$ の値を求めよ。またACの長さを求めよ。
(2) 四角形ABCDの面積 $S$ を求めよ。
(1) $\cos B$ の値を求めよ。またACの長さを求めよ。
(2) 四角形ABCDの面積 $S$ を求めよ。
【(1)の考え方と解答】
円に内接する四角形を描くときは,円を先に描くようにしよう。
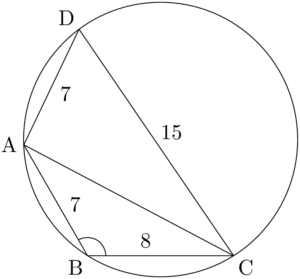
$\cos B$ を求めるために $\sankaku{ABC}$ に着目しよう。余弦定理より
円に内接する四角形を描くときは,円を先に描くようにしよう。

$\cos B$ を求めるために $\sankaku{ABC}$ に着目しよう。余弦定理より
\begin{align*}
&\text{AC}^2=7^2+8^2-2\Cdota7\Cdota8\cos B \\[4pt]&\text{AC}^2=113-112\cos B~\cdots\cdots①
\end{align*}
ACが分からないから,もう1本等式を作る必要がある。$\sankaku{ACD}$ に着目して,対角の和が $180\Deg$ であることを利用しよう。余弦定理より&\text{AC}^2=7^2+8^2-2\Cdota7\Cdota8\cos B \\[4pt]&\text{AC}^2=113-112\cos B~\cdots\cdots①
\end{align*}
\begin{align*}
&\text{AC}^2=7^2+15^2-2\Cdota7\Cdota15\cos D \\[4pt]&\text{AC}^2=274-210\cos(180\Deg-B) \\[4pt]&\text{AC}^2=274+210\cos B~\cdots\cdots②
\end{align*}
$②-①$ よりACを消去して&\text{AC}^2=7^2+15^2-2\Cdota7\Cdota15\cos D \\[4pt]&\text{AC}^2=274-210\cos(180\Deg-B) \\[4pt]&\text{AC}^2=274+210\cos B~\cdots\cdots②
\end{align*}
\begin{align*}
&161+322\cos B=0 \\[4pt]&\cos B=-\dfrac{1}{2}
\end{align*}
①に代入して&161+322\cos B=0 \\[4pt]&\cos B=-\dfrac{1}{2}
\end{align*}
\begin{align*}
\text{AC}^2&=113-112\Cdota\left(-\dfrac{1}{2}\right) \\[4pt]&=113+56=169
\end{align*}
$\text{AC}>0$ より $\text{AC}=13$\text{AC}^2&=113-112\Cdota\left(-\dfrac{1}{2}\right) \\[4pt]&=113+56=169
\end{align*}
(2) 四角形ABCDの面積 $S$ を求めよ。
【(2)の考え方と解答】
$\cos B$ の値が分かったから $\sin B$ の値も分かるけど,今回は $B$ が分かる。
$\cos B=-\dfrac{1}{2}$ より $B=120\Deg$ であるから,$D=60\Deg$ となる。
したがって
$\cos B$ の値が分かったから $\sin B$ の値も分かるけど,今回は $B$ が分かる。
$\cos B=-\dfrac{1}{2}$ より $B=120\Deg$ であるから,$D=60\Deg$ となる。
したがって
\begin{align*}
S&=\sankaku{ABC}+\sankaku{ACD} \\[4pt]&=\dfrac{1}{2}\Cdota7\Cdota8\sin120\Deg+\dfrac{1}{2}\Cdota7\Cdota15\sin60\Deg \\[4pt]&=14\sqrt{3}+\dfrac{105\sqrt{3}}{4}=\dfrac{161\sqrt{3}}{4}
\end{align*}
S&=\sankaku{ABC}+\sankaku{ACD} \\[4pt]&=\dfrac{1}{2}\Cdota7\Cdota8\sin120\Deg+\dfrac{1}{2}\Cdota7\Cdota15\sin60\Deg \\[4pt]&=14\sqrt{3}+\dfrac{105\sqrt{3}}{4}=\dfrac{161\sqrt{3}}{4}
\end{align*}

ヒロ
$\cos B$ から $B$ を求めることができない場合は,相互関係から $\sin B$ を求めよう。

ヒロ
今回は「那覇三角形」を知っていると,図を描きやすかっただろう。
円に内接する四角形に関する問題2

ヒロ
次の問題も実際に定期テストで出題された問題。
問題円に内接する四角形ABCDにおいて
\begin{align*}
\text{AB}=2,~\text{BC}=3,~\text{CD}=4,~\text{DA}=5
\end{align*}
であるとき,四角形ABCDの面積 $S$ を求めよ。\text{AB}=2,~\text{BC}=3,~\text{CD}=4,~\text{DA}=5
\end{align*}
【考え方と解答】
誘導がなくても,さっきと同じように解けるようにしよう。
図がないと考えにくい人は,それなりの図を描こう。
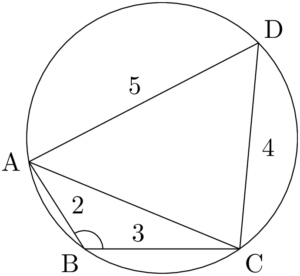
$\sankaku{ABC}$ において余弦定理より
誘導がなくても,さっきと同じように解けるようにしよう。
図がないと考えにくい人は,それなりの図を描こう。

$\sankaku{ABC}$ において余弦定理より
\begin{align*}
\text{AC}^2&=2^2+3^2-2\Cdota2\Cdota3\cos B \\[4pt]&=13-12\cos B~\cdots\cdots①
\end{align*}
また $\sankaku{ACD}$ において,余弦定理より\text{AC}^2&=2^2+3^2-2\Cdota2\Cdota3\cos B \\[4pt]&=13-12\cos B~\cdots\cdots①
\end{align*}
\begin{align*}
\text{AC}^2&=5^2+4^2-2\Cdota5\Cdota4\cos D \\[4pt]&=41+40\cos B~\cdots\cdots②
\end{align*}
$②-①$ より\text{AC}^2&=5^2+4^2-2\Cdota5\Cdota4\cos D \\[4pt]&=41+40\cos B~\cdots\cdots②
\end{align*}
\begin{align*}
&28+52\cos B=0 \\[4pt]&\cos B=-\dfrac{7}{13}
\end{align*}
$\sin B>0$ より&28+52\cos B=0 \\[4pt]&\cos B=-\dfrac{7}{13}
\end{align*}
\begin{align*}
\sin B&=\sqrt{1-\cos^2B} \\[4pt]&=\sqrt{1-\left(-\dfrac{7}{13}\right)^2} \\[4pt]&=\dfrac{2\sqrt{30}}{13}
\end{align*}
ここで\sin B&=\sqrt{1-\cos^2B} \\[4pt]&=\sqrt{1-\left(-\dfrac{7}{13}\right)^2} \\[4pt]&=\dfrac{2\sqrt{30}}{13}
\end{align*}
\begin{align*}
\sin D=\sin(180\Deg-B)=\sin B
\end{align*}
であることに注意すると,求める面積 $S$ は\sin D=\sin(180\Deg-B)=\sin B
\end{align*}
\begin{align*}
S&=\sankaku{ABC}+\sankaku{ACD} \\[4pt]&=\dfrac{1}{2}\Cdota2\Cdota3\sin B+\dfrac{1}{2}\Cdota5\Cdota4\sin D \\[4pt]&=13\sin B=13\Cdota\dfrac{2\sqrt{30}}{13} \\[4pt]&=2\sqrt{30}
\end{align*}
S&=\sankaku{ABC}+\sankaku{ACD} \\[4pt]&=\dfrac{1}{2}\Cdota2\Cdota3\sin B+\dfrac{1}{2}\Cdota5\Cdota4\sin D \\[4pt]&=13\sin B=13\Cdota\dfrac{2\sqrt{30}}{13} \\[4pt]&=2\sqrt{30}
\end{align*}