数学Ⅱで学習する面積を求める3分の1公式(1/3公式)の説明をします。3分の1公式は,センター試験の数学で面積を求める裏技公式として有名な公式の1つです。
放物線とその接線と $y$ 軸に平行な直線で囲まれる図形の面積を求めるときに,3分の1公式を使うことで,定積分の式を書かず,積分計算もせずに,速く楽に面積を求めることができます。
3分の1公式も6分の1公式と同様に十分使える形で,様々な大学入試で出題されています。公式が何故成り立つかを知ることは重要です。しかし,公式を単なる道具として使えることも重要です。特にセンター試験のような短時間で正確に答えを求めればよい試験に対しては,3分の1公式を使って時間を短縮しましょう。
3分の1公式の証明を知ることで,3分の1公式が成り立つことが当たり前だと感じることができるでしょう。
1999年のセンター試験数学ⅡBの問題を扱って説明します。
直線 $x=\dfrac{a}{2},~\ell$ および $C$ で囲まれた図形の面積 $S$ は $S=\dfrac{a^{\,\myBox{ア}}}{\myBox{イウ}}$である。ただし,$a$ は $0<a<2$ を満たす定数とする。
Contents
定積分で面積を求める(通常解法)

まずは図を描いて,どの図形の面積を求めるのか把握しよう。
y’=-2x+2
\end{align*}
y=2x
\end{align*}
よって,直線 $x=\dfrac{a}{2},~\ell$ および $C$ で囲まれた図形は下図の斜線部分となる。
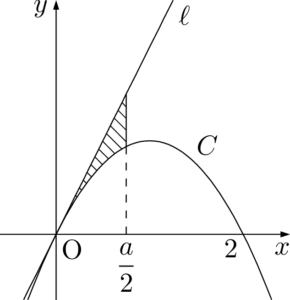
よって求める面積 $S$ は
S&=\dint{0}{\frac{a}{2}}\{2x-(-x^2+2x)\}\;dx \\[4pt]
&=\dint{0}{\frac{a}{2}}x^2\;dx \\[4pt]
&=\Tint{\dfrac{1}{3}x^3}{0}{\frac{a}{2}} \\[4pt]
&=\dfrac{1}{3}\left(\dfrac{a}{2}\right)^3 \\[4pt]
&=\dfrac{a^3}{24}
\end{align*}
放物線とその接線と $y$ 軸で囲まれた図形の面積を一般的に求める

一般的に考えてみよう。

まず接線 $\ell$ の方程式を求めよう。
f'(x)=2ax+b
\end{align*}
&y=(2at_1+b)(x-t_1)+a{t_1}^2+bt_1+c \\[4pt]
&y=(2at_1+b)x-a{t_1}^2+c
\end{align*}

図を描くと次のようになる。
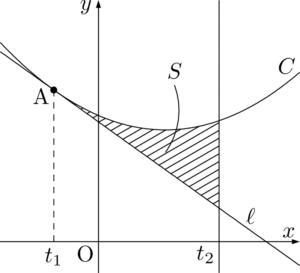
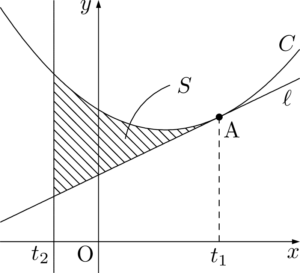

次に面積 $S$ を求めよう。
S&=\dint{t_1}{t_2}\bigl\{(ax^2+bx+c)-\{(2at_1+b)x-a{t_1}^2+c\}\bigr\}\;dx \\[4pt]
&=\dint{t_1}{t_2}(ax^2-2at_1x+a{t_1}^2)\;dx \\[4pt]
&=\dint{t_1}{t_2}a(x-t_1)^2\;dx \\[4pt]
&=\Tint{\dfrac{a}{3}(x-t_1)^3}{t_1}{t_2} \\[4pt]
&=\dfrac{a}{3}(t_2-t_1)^3
\end{align*}
S=\dfrac{a}{3}(t_1-t_2)^3
\end{align*}
接する2つの放物線と $y$ 軸で囲まれた図形の面積を一般的に求める

さらに放物線どうしが接する場合を考えてみよう。

$t_1<t_2$ の場合を考える。
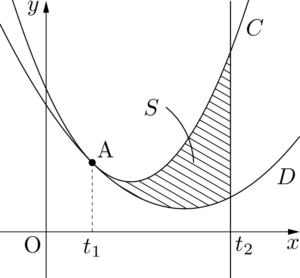
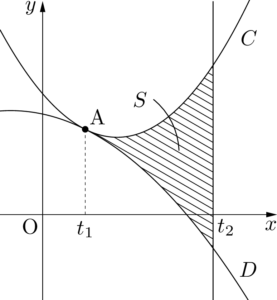
2つの放物線 $C,~D$ が $x=t_1$ の点で接しているから,方程式 $f(x)-g(x)=0$ は重解 $x=t_1$ をもつ。したがって,$f(x)-g(x)$ の $x^2$ の係数が $a-p$ になることを考えると
f(x)-g(x)=(a-p)(x-t_1)^2
\end{align*}
S&=\dint{t_1}{t_2}\{f(x)-g(x)\}\;dx \\[4pt]
&=\dint{t_1}{t_2}(a-p)(x-t_1)^2\;dx \\[4pt]
&=\Tint{\dfrac{a-p}{3}(x-t_1)^3}{t_1}{t_2} \\[4pt]
&=\dfrac{a-p}{3}(t_2-t_1)^3
\end{align*}
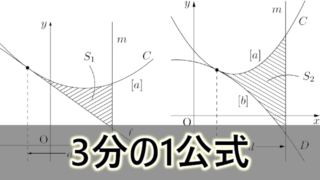
面積を求める3分の1公式

面積を求める3分の1公式を使えるようにしよう。
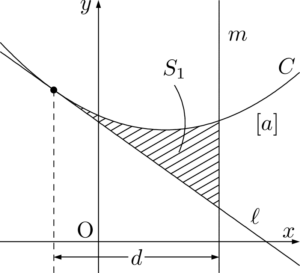
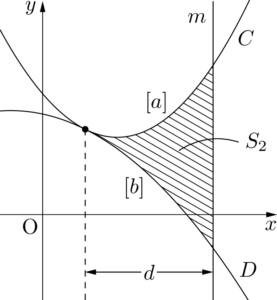
放物線 $C$ とその接線 $\ell$ および $y$ 軸に平行な直線 $m$ で囲まれた図形の面積 $S_1$ や接する2つの放物線 $C,~D$ と直線 $m$ で囲まれた図形の面積 $S_2$ は,次のように表すことができる。図中の $[a]$, $[b]$ は $x^2$ の係数を表す。
S_1=\dfrac{\abs{a}}{3}d^3,~S_2=\dfrac{\abs{a-b}}{3}d^3
\end{align*}
3分の1公式を利用した解法(裏技解法)
放物線 $y=-x^2+2x$ を $C$ とし,原点Oにおける $C$ の接線を $\ell$ とする。
直線 $x=\dfrac{a}{2},~\ell$ および $C$ で囲まれた図形の面積 $S$ は $S=\dfrac{a^{\,\myBox{ア}}}{\myBox{イウ}}$である。ただし,$a$ は $0<a<2$ を満たす定数とする。

それでは3分の1公式を利用して解いてみよう。

$x^2$ の係数は $-1$ で,原点が接点だから,$d=\dfrac{a}{2}$ となる。よって
S=\dfrac{\abs{-1}}{3}\left(\dfrac{a}{2}\right)^3=\dfrac{a^3}{24}
\end{align*}

実際には,接線 $\ell$ の方程式については,$C$ の方程式を見た瞬間に分かるけど,また,別の話なのでここでは省略する。
被積分関数を因数分解したときの形を知って3分の1公式を理解しよう

ある図形の面積を求めるときは,定積分することによって求める。

多項式で表された2つの曲線(直線を含む)が接するときは,2つの関数の差が被積分関数となる。これを因数分解すると2乗の因数が現れることを常識にしておこう。

これによって,3分の1公式も理解できるはず。
(ax^2+bx+c)-(px+q)=a(x-t)^2
\end{align*}
また,放物線 $y=ax^2+bx+c$ と放物線 $y=px^2+qx+r$ が $x$ 座標が $t$ である点で接しているとき
(ax^2+bx+c)-(px^2+qx+r)=(a-p)(x-t)^2
\end{align*}

一般化すると次のようになる。
f(x)-g(x)=(x-t)^2Q(x)
\end{align*}

これをしっかり理解すると,1つの式を見ても,思うこと・感じること・考えることが色々あって楽しくなる。いくつか例を挙げておこう。

即座に式を見てグラフが想像できることが重要だね。

$y=ax^2+bx+c$ の $b$ って何ですか?と聞く人がいるけど,これからは「点 $(0,~c)$ における接線の傾きだよ」と答えてあげよう。

定数項も含めて考えると,$y=bx+c$ は $y=ax^2+bx+c$ 上の点 $(0,~c)$ における接線であることを理解しておくのが良い。

少し言い方を変えると,$y=f(x)$ の点 $(-1,~f(-1))$ における接線の方程式は,$f(x)$ を $(x+1)^2$ で割ることで求めることができる。また,副産物として,もう1つの交点の $x$ 座標まで求められるっていうこと。
まとめ

面積を求める3分の1公式を適切に使うことによって,圧倒的に楽に速く面積を求めることができる。

また,2曲線 $y=f(x),~y=g(x)$ が接するときは $f(x)-g(x)$ を因数分解すると2乗のカタマリを因数にもつことを常識にしよう。