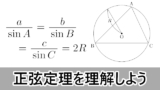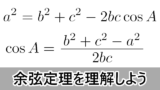ここでは三角比を含む比例式の問題について解説します。
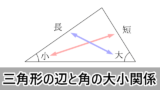
次の記事の三角形の辺と角の大小関係に関する知識が前提となっています。
また，正弦定理や余弦定理の復習は次の記事でして下さい。
【数学IA】正弦定理を理解しよう
ここでは正弦定理について説明します。 正弦とはサインのことで，定理の名前の通り，サインに関する定理が「正弦定理」です。 直角三角形だけでなく，一般的な三角形に成り立つ定理なので，様々な問題で利用することになります。 定理の内容を理解して使え...
methodology.site
2020.06.05
【数学IA】余弦定理を理解しよう
ここでは余弦定理について説明します。 余弦とはコサインのことで，定理の名前の通り，コサインに関する定理が「余弦定理」です。 正弦定理と同様に，直角三角形だけでなく一般的な三角形に成り立つ定理なので，様々な問題で利用することになります。 定理...
methodology.site
2020.06.06
Contents
- ページ1
- 1 比例式とは
- ページ2
- 1 三角形の最大角に関する問題
比例式とは
ヒロ
まずは比例式とは何かを知っておこう。
比例式$a:b:c=d:e:f$ のように比と比と等号で結んだ等式を比例式という。これは分数の等式
$\dfrac{a}{d}$, $\dfrac{b}{e}$, $\dfrac{c}{f}$ の3つの式が等しいから $k$ とおくと，
\begin{align*}
\dfrac{a}{d}=\dfrac{b}{e}=\dfrac{c}{f}
\end{align*}
が成り立つことと同じことを表している。\dfrac{a}{d}=\dfrac{b}{e}=\dfrac{c}{f}
\end{align*}
$\dfrac{a}{d}$, $\dfrac{b}{e}$, $\dfrac{c}{f}$ の3つの式が等しいから $k$ とおくと，
\begin{align*}
\dfrac{a}{d}=k,~\dfrac{b}{e}=k,~\dfrac{c}{f}=k
\end{align*}
となり，\dfrac{a}{d}=k,~\dfrac{b}{e}=k,~\dfrac{c}{f}=k
\end{align*}
\begin{align*}
a=kd,~b=ke,~c=kf
\end{align*}
と変形できる。この変形には文字数を減らすことができるメリットがある。今回の例では，6文字だったものが $k$ とおくことで4文字になる。a=kd,~b=ke,~c=kf
\end{align*}
ヒロ
比例式を見たときには $k$ とおくことが基本手法となることを知っておこう。