ここでは正弦定理について説明します。
正弦とはサインのことで,定理の名前の通り,サインに関する定理が「正弦定理」です。
直角三角形だけでなく,一般的な三角形に成り立つ定理なので,様々な問題で利用することになります。
定理の内容を理解して使えるようにしましょう。
正弦定理とは

早速,正弦定理とはどういうものかを知ろう。
\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R
\end{align*}
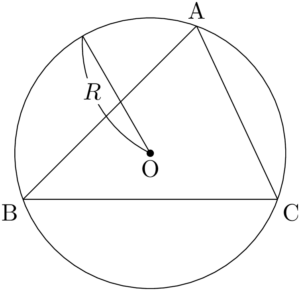

3本の等式を覚える必要はなく,$\dfrac{a}{\sin A}=2R$ を覚えていれば $\dfrac{b}{\sin B}=2R$ が成り立つことを当たり前に感じられるようになろう。

頂点Aの「A」はただの「ラベル」であり,$A$ と $a$ は向かい合う角と辺の長さを表しているだけで,表現の都合上,具体的に表しているだけだ。

それでは正弦定理の証明をしておこう。

$A$ が鋭角・直角・鈍角のときで場合分けをして,等式 $a=2R\sin A$ が成り立つことを証明しよう。
(i) $A=90\Deg$ のとき
BCが $\sankaku{ABC}$ の外接円の直径となるから,$a=2R$ である。
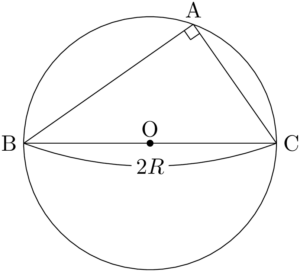
$\sin A=\sin90\Deg=1$ より
a=2R\sin A
\end{align*}
(ii) $A<90\Deg$ のとき 点Bを通る直径をBDとすると,$\kaku{BCD}=90\Deg$ である。$\ko{BC}$ に対して円周角の定理より,$\kaku{BDC}=A$ となる。
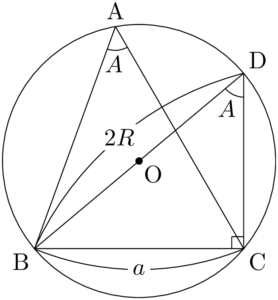
よって,$a=2R\sin A$ が成り立つ。
(iii) $A>90\Deg$ のとき
点Bを通る直径をBDとすると,$\kaku{BCD}=90\Deg$ である。四角形ABDCは円に内接する四角形であるから,対角の和は $180\Deg$ であり,$\kaku{BDC}=180\Deg-A$ となる。
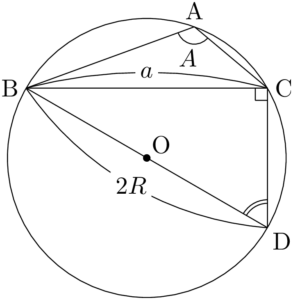
したがって
a&=2R\sin(180\Deg-A) \\[4pt]
&=2R\sin A
\end{align*}
a=2R\sin A
\end{align*}
b=2R\sin B,~c=2R\sin C
\end{align*}

教科書に書かれている正弦定理は $\dfrac{a}{\sin A}=2R$ の形で書かれていて,これだけを覚えているからか,この形から変形しないと他の形の式を書けない人が多い。

求めたいものに応じて,$a=2R\sin A$,$\sin A=\dfrac{a}{2R}$,$R=\dfrac{a}{2\sin A}$ を使い分けられるようになろう。
- 辺の長さを求めたいとき
$a=2R\sin A$ - 角度を求めたいとき
$\sin A=\dfrac{a}{2R}$ - 外接円の半径を求めたいとき
$R=\dfrac{a}{2\sin A}$
正弦定理を利用する問題

それでは問題を解いて正弦定理の使い方を覚えていこう。
三角形の2つの角の大きさが与えられたときは,残りの1つの角の大きさも分かることに注意しよう。
$A+B+C=180\Deg$ より
&A+60\Deg+75\Deg=180\Deg \\[4pt]
&A=45\Deg
\end{align*}
&\dfrac{a}{\sin A}=\dfrac{b}{\sin B} \\[4pt]
&\dfrac{10}{\sin 45\Deg}=\dfrac{b}{\sin 60\Deg} \\[4pt]
&b=10\sin60\Deg\Cdota\dfrac{1}{\sin45\Deg} \\[4pt]
&b=10\Cdota\dfrac{\sqrt{3}}{2}\Cdota\sqrt{2}=5\sqrt{6}
\end{align*}

最初に正弦定理の証明をしたけど,次の記事でも触れている別の捉え方も理解しておこう。
$\sankaku{ABC}$ において点Aから直線BCに垂線AHを下ろす。Hが辺BC上にあるときとないときの2通りが考えられ,次の図のようになる。
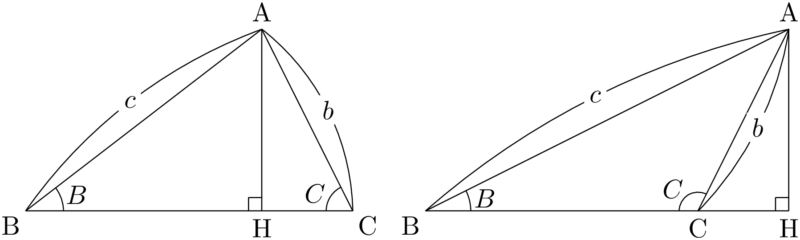
Hが辺BC上にないときは,HはCの延長側にあるときとBの延長側にあるときの2通りがあるが,どちらでもほとんど同じなのでここではCの延長側にある状態を描いている。
AHの長さについて考える。上の左の図において $\sankaku{ABH}$ に着目すると
\text{AH}&=\text{AB}\sin\kaku{ABH} \\[4pt]
&=c\sin B
\end{align*}
\text{AH}&=\text{AC}\sin\kaku{ACH} \\[4pt]
&=b\sin C
\end{align*}
\text{AH}&=\text{AB}\sin\kaku{ABH} \\[4pt]
&=c\sin B
\end{align*}
\text{AH}&=\text{AC}\sin\kaku{ACH} \\[4pt]
&=b\sin(180\Deg-C) \\[4pt]
&=b\sin C
\end{align*}
AHの表し方が2通りあるが,当然同じ長さであるから
c\sin B=b\sin C
\end{align*}
同様にして,点CとABとの距離(ABを底辺と見た高さ)を考えると
a\sin B=b\sin A
\end{align*}
このように捉えることで,式を扱う上でのメリットが生まれる。
従来の「$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}$」の形だとサインが分母にあるため,繁分数(分母が分数になっているもの)になり,書く上でも計算をする上でも少し鬱陶しい。一方で三角形の高さに着目した「$a\sin B=b\sin A$」の形だと,そういう鬱陶しさはなくなるのと同時に,意味も理解しているため「忘れる」ということがなくなる。そもそも「覚えていない」から「忘れる」ことができない。
あとは一瞬でこの考え方をすることができるように訓練するだけで「正弦定理なんて簡単だ」と思えるようになるはずである。
正弦定理を利用する問題2

次は外接円の半径を求める問題を解いてみよう。
「外接円の半径を求める問題」においては正弦定理を利用するのが1つの考え方。また,教科書に書かれている「$2R=\dfrac{a}{\sin A}$」を利用する人が圧倒的多数だけど,「$R=\dfrac{a}{2\sin A}$」を利用することを勧める。
理由は $A$ が三角定規に現れる角度である問題が多く,そのような問題では前に2が付くことで分数でなくなるから。つまり繁分数にならないから,計算をする上で鬱陶しくならない。さらに,$2R$ で求めた場合,計算に意識が向くことで「直径を求めていること」に気付かず2で割るのを忘れてしまう可能性がある。「注意」すれば良いだけであるが,求めるものを明確に捉えて工夫することで,直径を求めてしまうリスクがなくなり,計算が楽になるのであれば「$R=\dfrac{a}{2\sin A}$」を利用することがベストではないだろうか。
ということで,当サイトでは今後も「$R=\dfrac{a}{2\sin A}$」の形を積極的に使用していく。
この問題の解答は次のようになる。
正弦定理より
R&=\dfrac{a}{2\sin A} \\[4pt]
&=\dfrac{6}{2\Cdot\dfrac{1}{2}}=6
\end{align*}

30°の対辺の長さが外接円の半径であることは常識にしても良いだろう。
30°,60°,90°の直角三角形ABCとその外接円を考える。$\kaku{ACB}=90\Deg$ であるから,ABが直径となる。
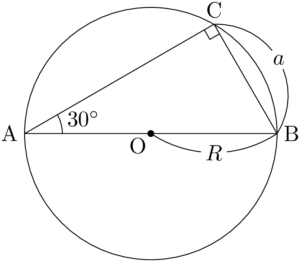
2点O, Cを結ぶと,円周角の定理より $\kaku{BOC}=60\Deg$ となる。
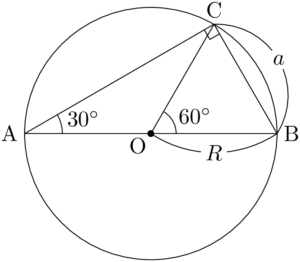
OCの長さも外接円の半径に等しいから,$\sankaku{OBC}$ は正三角形である。
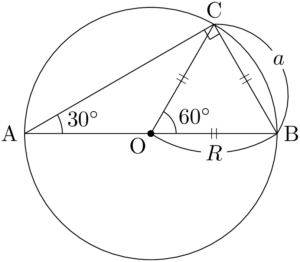
したがって,$a=R$ が成り立つ。

こういうことを言うと「丸覚えしても意味がない」という人がいるが,論点がずれている。上で説明した内容や図を当たり前だと感じられるくらいの図形的感覚を持ちましょうよと提案しているだけである。



















