ここでは余弦定理について説明します。
余弦とはコサインのことで,定理の名前の通り,コサインに関する定理が「余弦定理」です。
正弦定理と同様に,直角三角形だけでなく一般的な三角形に成り立つ定理なので,様々な問題で利用することになります。
https://methodology.site/the-law-of-sines
定理の内容を理解して使えるようにしましょう。
余弦定理とは

早速,余弦定理とはどういうものかを知ろう。
&a^2=b^2+c^2-2bc\cos A \\[4pt]
&\cos A=\dfrac{b^2+c^2-a^2}{2bc}
\end{align*}

教科書には「$b^2=c^2+a^2-2ca\cos B$」なども載っているが,別々に覚えるなんてことは無意味なので辞めましょう。

辺の長さを求めたいときは $a^2=$ で始まる式,角度を求めたいときは $\cos A=$ で始まる式,という具合に使いこなせるようにするべきである。

上の式は余弦定理の公式として書かれているためか,覚えている人は多い。

しかし,下の式については,上の式を変形しないと書けない人がいる。個人的には,書くコツを知らないだけだと思う。
$\cos A=$ で始まる式を書きたいときは,$A$ を挟む2辺の長さは $b,~c$ である。単純に,角 $A$ にある頂点AのアルファベットA以外のBとCを小文字にするだけで良い。この2つの $b,~c$ と2を掛けたものを分母に書く。
\cos A=\dfrac{\qquad\qquad\qquad\qquad}{2bc}
\end{align*}
\cos A=\dfrac{b^2+c^2\qquad}{2bc}
\end{align*}
\cos A=\dfrac{b^2+c^2-a^2}{2bc}
\end{align*}

それでは余弦定理の証明をしておこう。

$A$ が鋭角・直角・鈍角のときで場合分けをして,等式 $a^2=b^2+c^2-2bc\cos A$ が成り立つことを証明しよう。
(i) $A=90\Deg$ のとき
三平方の定理より $a^2=b^2+c^2$ が成り立つ。$\cos A=\cos90\Deg=0$ より
a^2=b^2+c^2-2bc\cos A
\end{align*}
(ii) $A<90\Deg$ のとき 頂点Cから直線ABに垂線CHを下ろす。Hが辺AB上にあるときとないときの2通りが考えられ,次の図のようになる。

まずは左の図のときを考える。$\sankaku{ACH}$ に着目すると
(iii) $A>90\Deg$ のとき
頂点Cから直線ABに垂線CHを下ろすと次のようになる。

(ii)と同様にして $\sankaku{ACH}$ に着目すると
\text{AH}&=\text{AC}\cos\kaku{CAH} \\[4pt]
&=b\cos(180\Deg-A) \\[4pt]
&=-b\cos A \\[4pt]
\text{CH}&=\text{AC}\sin\kaku{CAH} \\[4pt]
&=b\sin(180\Deg-A) \\[4pt]
&=b\sin A
\end{align*}
\text{BH}&=\text{AH}+\text{AB} \\[4pt]
&=-b\cos A+c
\end{align*}
\text{BC}^2&=\text{BH}^2+\text{CH}^2 \\[4pt]
&=(-b\cos A+c)^2+(b\sin A)^2 \\[4pt]
&=b^2\cos^2A-2bc\cos A+c^2+b^2\sin^2A \\[4pt]
&=b^2-2bc\cos A+c^2
\end{align*}
(i)~(iii)より,三角形ABCに対して
a^2=b^2+c^2-2bc\cos A
\end{align*}

教科書に書かれている余弦定理は $a^2=b^2+c^2-2bc\cos A$ の形で書かれていて,正弦定理と同様に,これだけを覚えているからか,この形から変形しないと他の形の式を書けない人が多い。

求めたいものに応じて,$a^2=b^2+c^2-2bc\cos A$ と $\cos A=\dfrac{b^2+c^2-a^2}{2bc}$ を使い分けられるようになろう。
- 辺の長さを求めたいとき
$a^2=b^2+c^2-2bc\cos A$ - 角度を求めたいとき
$\cos A=\dfrac{b^2+c^2-a^2}{2bc}$
余弦定理を利用する問題

それでは問題を解いて余弦定理の使い方を覚えていこう。

与えられている条件は,「2つの辺の長さとその間の角」であり,三角形の合同条件の1つである。

つまり与えられている条件によって $\sankaku{ABC}$ は1つに決まることになるから,条件を満たす $a$ の値もただ1つのみ存在することになる。

実際に余弦定理を用いて求めてみよう。
余弦定理より
a^2&=b^2+c^2-2bc\cos A \\[4pt]
&=2^2+3^2-2\Cdota2\Cdota3\cos60\Deg \\[4pt]
&=4+9-12\Cdota\dfrac{1}{2}=7
\end{align*}

$a^2=7$ は $a$ の2次方程式だから,方程式の解は2つあるが,求める $a$ は辺の長さだから正の値の方だけが解として適していることになる。

このような細かい部分に対しても気を配るようにしよう。

また「余弦定理を忘れると詰む」と思っている人が多いが,実はそうではない。

個人的には「余弦定理を忘れたからなどとつまらない理由で問題を解けなかったことを正当化するな」と言いたい。

今回の問題の別解を示しておこう。
今回は与えられている角が $60\Deg$ であるから,30°,60°,90°の直角三角形を思い浮かべよう。
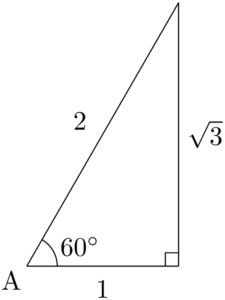
ここで与えられている条件の1つ「$b=2$」が計算をする上で都合が良い。斜辺の長さが $b$ になるようにしよう。つまり $\text{AC}=2$ であるから,点Cの位置が決まる。したがって,点Bは長さ1の底辺上にあるか,破線で示したその延長上にあることが分かる。
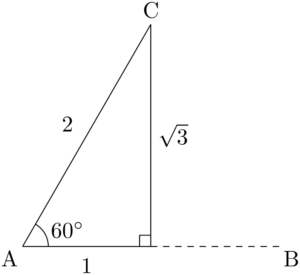
$c=3$ であることから点Bの位置も次のように決まるから,$\sankaku{ABC}$ をかなり正確に描くことができる。
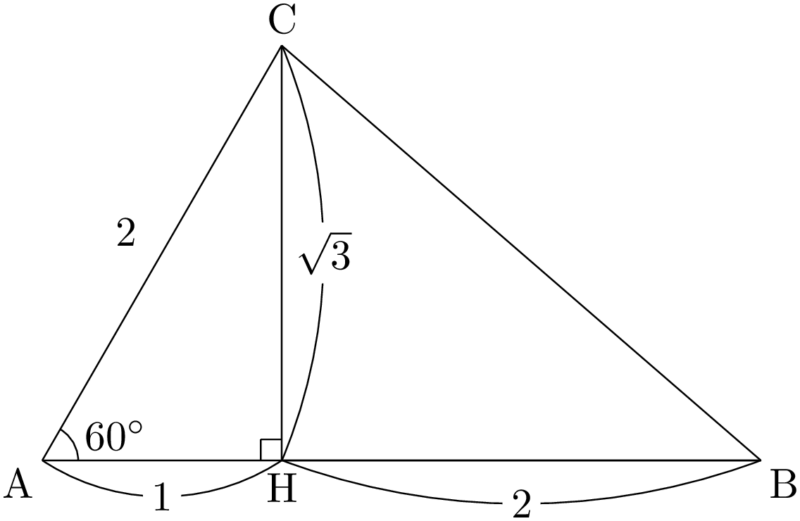
$\sankaku{BCH}$ に着目して,三平方の定理を用いることによって
&\text{BC}=\sqrt{\text{BH}^2+\text{CH}^2} \\[4pt]
&a=\sqrt{2^2+(\sqrt{3})^2}=\sqrt{7}
\end{align*}

このように解くことで,余弦定理を忘れても何も問題がないことになる。

既に気付いているだろうが,この手順は「余弦定理の証明」の方法と同じである。

三角定規に現れる角ではない場合はサインやコサイン(場合によってはタンジェント)の三角比が与えられているはずで,それを利用して同じように図を描くことができる。

具体的にどのようにするのかについては,次の記事が参考になるだろう。



余弦定理なんて「三平方の定理を2回使ったもの」という認識でいれば忘れてもどうにかなるわけで,何回も「余弦定理の証明」をすることになるから,余弦定理を覚えることもできるのではないだろうか。
第1余弦定理とは

さて,ここで少し話が変わるが・・・

正弦定理の記事で,三角形の高さに着目した捉え方を紹介したが,三角形の底辺に着目するとコサインに関する等式が得られる。

実は最初に扱った余弦定理は正確には「第2余弦定理」と呼ばれるものである。

「第2」ということはその前に「第1」があるはずである。それが三角形の底辺に着目して得られるコサインに関する等式である。
$\sankaku{ABC}$ において点Aから直線BCに垂線AHを下ろす。Hが辺BC上にあるときとないときの2通りが考えられ,次の図のようになる。
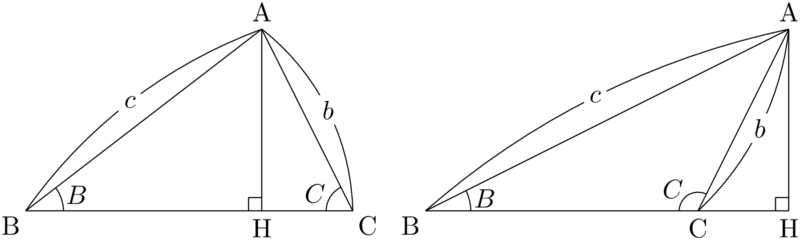
Hが辺BC上にないときは,HはCの延長側にあるときとBの延長側にあるときの2通りがあるが,どちらも同じなのでここではCの延長側にある状態を描いている。
ここでBCの長さを考える。上の左の図において $\sankaku{ABH}$ に着目すると
\text{BH}&=\text{AB}\cos\kaku{ABH} \\[4pt]
&=c\cos B
\end{align*}
\text{CH}&=\text{AC}\cos\kaku{ACH} \\[4pt]
&=b\cos C
\end{align*}
\text{BC}&=\text{BH}+\text{CH} \\[4pt]
&=c\cos B+b\cos C
\end{align*}
a=c\cos B+b\cos C
\end{align*}
また,上の右の図において $\sankaku{ABH}$ に着目すると
\text{BH}&=\text{AB}\cos B \\[4pt]
&=c\cos B
\end{align*}
\text{CH}&=\text{AC}\cos\kaku{ACH} \\[4pt]
&=b\cos(180\Deg-C) \\[4pt]
&=-b\cos C
\end{align*}
&\text{BC}=\text{BH}-\text{CH} \\[4pt]
&a=c\cos B-(-b\cos C) \\[4pt]
&a=c\cos B+b\cos C
\end{align*}

三角形の底辺の長さをコサインで表した等式(第1余弦定理)も使いこなせるようになると良いだろう。
余弦定理を利用する問題2

この問題では,三角形の合同条件ではない条件が与えられているため,三角形の形が1つに定まらない可能性がある。

したがって,$a$ の値も2つあるかもしれないと思って解いていこう。
$a$ を求めるからといって「$a^2=$ で始まる式を使う」という状態にならないようにしよう。余弦定理のどの形を利用するかは与えられている角に着目しよう。今回は $B=60\Deg$ が与えられているから,Bの対辺の長さに着目して $b^2=$ で始まる式を利用しよう。
余弦定理より
&b^2=c^2+a^2-2ca\cos B \\[4pt]
&7^2=8^2+a^2-2\Cdota8a\Cdota\cos60\Deg \\[4pt]
&49=64+a^2-16a\Cdota\dfrac{1}{2} \\[4pt]
&a^2-8a+15=0 \\[4pt]
&(a-3)(a-5)=0 \\[4pt]
&a=3,~5
\end{align*}

最初の予想通り,$a$ の値が2つ出てきて,これはどちらも取り得る値である。

ちなみに名古屋三角形などの「知識」があると問題を読んだ直後に「$a$ は3か5だなぁ」と分かるようになる。

詳しいことについては次の記事に書いているので参考にして欲しい。



















