ここでは2次方程式の解の配置問題とよばれる問題を解説します。
2次方程式の解は2次関数のグラフと $x$ 軸の共有点の $x$ 座標であるため,単に「2次方程式の解」として考えることは少ないです。
ほとんどの場合,2次関数のグラフを利用して考えます。
2次関数のグラフは放物線であり,解の配置問題では次の4つに着目して考えます。
- 上に凸か下に凸か
- 軸の位置(頂点の $x$ 座標)
- 頂点の $y$ 座標(判別式で代用可能)
- 考える範囲の端点の $y$ 座標
問題で与えられた条件を満たすのは,グラフがどのようになるときかを考えましょう。
慣れないうちはかなり難しく感じますが,諦めなければいつかは解けるようになるでしょう。
また,上に凸か下に凸かを意識していないと,グラフが下に凸の放物線として考えてしまい,符号が逆になってしまうことがあるので注意しましょう。
Contents
2次方程式の解の配置問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題2次方程式 $x^2-2ax+4a+1=0$ の1つの解が $-1$ と0の間にあり,他の解が0と1の間にあるとき,定数 $a$ の値の範囲を求めよ。
【考え方と解答】
$C:y=x^2-2ax+4a+1$ のグラフと $x$ 軸の共有点が2点あり,そのうち1つが $-1<x<0$ にあり,もう1つが $0<x<1$ にあるような条件を考える。 $C$ は下に凸の放物線だから,次のような状態にあることが分かる。
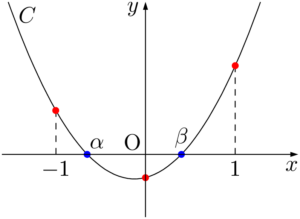
ここで,説明のために $C$ と $x$ 軸の共有点の $x$ 座標を $\alpha,~\beta~(\alpha<\beta)$ とおく。 問題文の条件から,青丸で示した2つの解 $\alpha,~\beta$ に着目して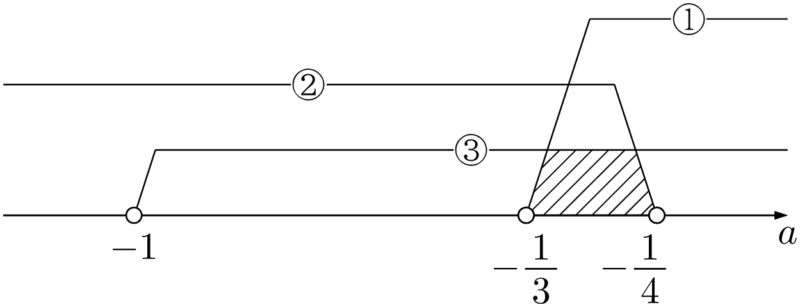
①,②,③より,求める $a$ の値の範囲は
$C:y=x^2-2ax+4a+1$ のグラフと $x$ 軸の共有点が2点あり,そのうち1つが $-1<x<0$ にあり,もう1つが $0<x<1$ にあるような条件を考える。 $C$ は下に凸の放物線だから,次のような状態にあることが分かる。

ここで,説明のために $C$ と $x$ 軸の共有点の $x$ 座標を $\alpha,~\beta~(\alpha<\beta)$ とおく。 問題文の条件から,青丸で示した2つの解 $\alpha,~\beta$ に着目して
\begin{align*} -1<\alpha<0~~かつ~~0<\beta<1 \end{align*}
という不等式を立てて考える人がいるが,これは結構大変である。 解の配置問題では,青丸の解そのものではなく,頂点や端点に着目する方が楽である。この問題では,赤丸で示した $-1<x<0$ と $0<x<1$ の端点に着目して考える。 $f(x)=x^2-2ax+4a+1$ とおく。 $-1<\alpha<0$ となるのは,$f(-1)>0$ かつ $f(0)<0$ を満たすときである。また,$0<\beta<1$ となるのは,$f(0)<0$ かつ $f(1)>0$ を満たすときである。 すなわち,$-1<\alpha<0~~かつ~~0<\beta<1$ となるのは \begin{align*} f(-1)>0~~かつ~~f(0)<0~~かつ~~f(1)>0 \end{align*}
を満たすときである。ここで \begin{align*} &f(-1)=1+2a+4a+1=6a+2 \\[4pt] &f(0)=4a+1 \\[4pt] &f(1)=1-2a+4a+1=2a+2 \end{align*}
である。 $f(-1)>0$ より \begin{align*} &6a+2>0 \\[4pt] &a>-\dfrac{1}{3}~\cdots\cdots① \end{align*}
$f(0)<0$ より \begin{align*} &4a+1<0 \\[4pt] &a<-\dfrac{1}{4}~\cdots\cdots② \end{align*}
$f(1)>0$ より \begin{align*} &2a+2>0 \\[4pt] &a>-1~\cdots\cdots③ \end{align*}

①,②,③より,求める $a$ の値の範囲は
\begin{align*} -\dfrac{1}{3}<a<-\dfrac{1}{4} \end{align*}

ヒロ
この問題では,端点に着目することで解くことができ,軸の位置について考える必要はない。

ヒロ
というか,軸の方程式は $x=a$ であり,軸の存在範囲が始めから正確に分かるなら,そのまま答えを求めることができてしまう。

ヒロ
また,判別式については,$f(-1)>0,~f(0)<0,~f(1)>0$ を考えた時点で $D>0$ という条件を含んでいる。

ヒロ
言い換えると $D>0$ より厳しい条件を考えているから判別式について考える意味がない。

ヒロ
解そのものに着目して不等式を立てた場合は「大変」と言ったけど,どれくらい大変なのかを見る機会は少ないだろう。

ヒロ
ということで,ここでやっておくことにする。
【解に着目した解法】
$x^2-2ax+4a+1=0$ が異なる2解をもつから,判別式を $D$ とすると $D>0$ である。
2つの解の条件より
$x^2-2ax+4a+1=0$ が異なる2解をもつから,判別式を $D$ とすると $D>0$ である。
\begin{align*} &\dfrac{D}{4}=a^2-(4a+1)>0 \\[4pt] &a^2-4a-1>0 \\[4pt] &a<2-\sqrt{5},~2+\sqrt{5}<a \end{align*}
この条件のもとで,方程式を解くと \begin{align*} x=a\pm\sqrt{a^2-4a-1} \end{align*}
となり,$\alpha,~\beta~(\alpha<\beta)$ とおく。2つの解の条件より
\begin{align*} -1<\alpha<0~~かつ~~0<\beta<1 \end{align*}
$-1<\alpha<0$ より \begin{align*} &-1<a-\sqrt{a^2-4a-1}<0 \\[4pt] &\begin{cases} \sqrt{a^2-4a-1}<a+1 &~\cdots\cdots① \\[4pt] a<\sqrt{a^2-4a-1} &~\cdots\cdots② \end{cases} \end{align*}
①の左辺は正であるから,右辺も正である。よって,$a>-1$ のときを考える。両辺を2乗すると \begin{align*} &a^2-4a-1<(a+1)^2 \\[4pt] &a^2-4a-1<a^2+2a+1 \\[4pt] &-6a<2 \\[4pt] &a>-\dfrac{1}{3} \end{align*}
$a>-1$ との共通部分を考えて,$a>-\dfrac{1}{3}$次に②を解く。
$a<2-\sqrt{5}$ のとき,②の左辺は負で右辺は正であるから,②は成り立つ。$2+\sqrt{5}<a$ のとき,右辺は $a$ より小さい値であるから②は成り立たない。
したがって,②の解は $a<2-\sqrt{5}$ である。
①と②の共通部分を求める。
$2-\sqrt{5}\fallingdotseq2-2.2\cdots\fallingdotseq-0.2\cdots$ より $-\dfrac{1}{3}<2-\sqrt{5}$ である。
よって,①と②をともに満たす $a$ の値の範囲は $-\dfrac{1}{3}<a<2-\sqrt{5}~\cdots\cdots③$
次に $0<\beta<1$ を考える。
\begin{align*} &0<a+\sqrt{a^2-4a-1}<1 \\[4pt] &\begin{cases} -a<\sqrt{a^2-4a-1} &~\cdots\cdots④ \\[4pt] \sqrt{a^2-4a-1}<-a+1 &~\cdots\cdots⑤ \end{cases} \end{align*}
④を解く。
$a<2-\sqrt{5}$ のとき,④の両辺は正であるから2乗して
\begin{align*} &a^2<a^2-4a-1 \\[4pt] &a<-\dfrac{1}{4} \end{align*}
$-\dfrac{1}{4}<2-\sqrt{5}$ であるから,$a<-\dfrac{1}{4}$$2+\sqrt{5}<a$ のとき,④の左辺は負で右辺は正であるから,④は成り立つ。
したがって,$a<-\dfrac{1}{4},~2+\sqrt{5}<a~\cdots\cdots④’$
次に⑤を解く。
$a<2-\sqrt{5}$ のとき,⑤の両辺は正であるから2乗して
\begin{align*} &a^2-4a-1<(-a+1)^2 \\[4pt] &a^2-4a-1<a^2-2a+1 \\[4pt] &-2a<2 \\[4pt] &a>-1 \end{align*}
よって,$-1<a<2-\sqrt{5}$$2+\sqrt{5}<a$ のとき,⑤の左辺は正で右辺は負であるから⑤は成り立たない。
よって,⑤の解は $-1<a<2-\sqrt{5}~\cdots\cdots⑤’$
したがって④と⑤をともに満たす $a$ の値の範囲は,④’と⑤’より $a<-\dfrac{1}{4}~\cdots\cdots⑥$
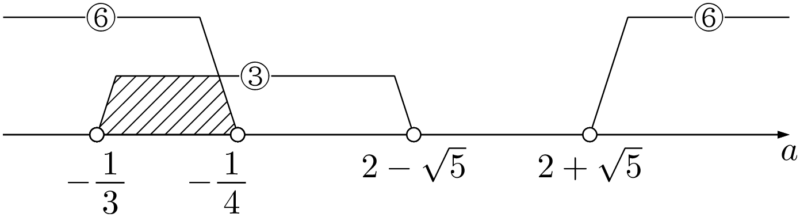
求めるものは③と⑥をともに満たす $a$ の値の範囲であるから $-\dfrac{1}{3}<a<-\dfrac{1}{4}$


ヒロ
このように計算が大変でも「立式が楽だから」という理由でこの方法で今後も解くだろうか?

ヒロ
「どうしてもこの方法で解く!」と強い意志を持っているならそれで良い。しかし,この方法で解けるなら,楽な解法でも解けるだろう。
2次方程式の解の配置問題2

ヒロ
次も定期テストで出題された問題。
問題2次方程式 $x^2-2ax+a=0$ が $-2<x<2$ の範囲に異なる2つの実数解をもつように定数 $a$ の値の範囲を求めよ。
【考え方と解答】
$C:y=x^2-2ax+a$ のグラフと $x$ 軸が $-2<x<2$ の範囲で異なる2点で交わるような $a$ の値の範囲を求める。 条件をみたすとき $C$ のグラフは次のようになる。
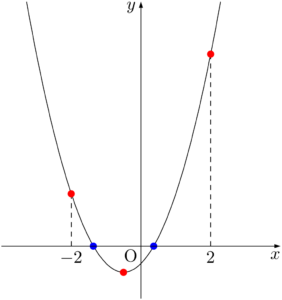
2つの実数解(青丸)が $-2<x<2$ にあるような条件を赤丸で示した端点と頂点で考える。 $f(x)=x^2-2ax+a$ とおく。 端点に着目すると,条件をみたすのは $f(-2)>0$ かつ $f(2)>0$ のときであることが分かる。 また頂点に着目すると,条件をみたすのは軸(頂点の $x$ 座標)は $-2<x<2$ の範囲にあり,頂点の $y$ 座標は負のとき(判別式 $D$ を利用する場合は $D>0$)である。 つまり,条件をみたすのは,次の4つの不等式が成り立つときである。
$C:y=x^2-2ax+a$ のグラフと $x$ 軸が $-2<x<2$ の範囲で異なる2点で交わるような $a$ の値の範囲を求める。 条件をみたすとき $C$ のグラフは次のようになる。

2つの実数解(青丸)が $-2<x<2$ にあるような条件を赤丸で示した端点と頂点で考える。 $f(x)=x^2-2ax+a$ とおく。 端点に着目すると,条件をみたすのは $f(-2)>0$ かつ $f(2)>0$ のときであることが分かる。 また頂点に着目すると,条件をみたすのは軸(頂点の $x$ 座標)は $-2<x<2$ の範囲にあり,頂点の $y$ 座標は負のとき(判別式 $D$ を利用する場合は $D>0$)である。 つまり,条件をみたすのは,次の4つの不等式が成り立つときである。
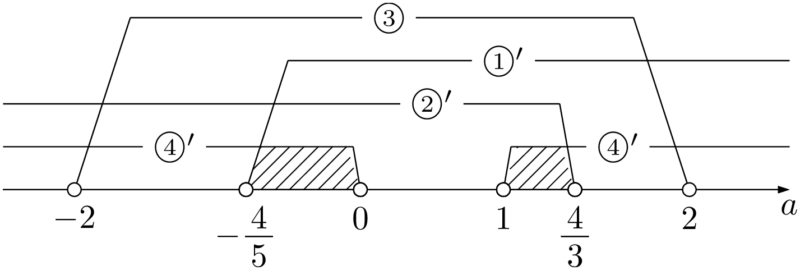
\begin{align*} \begin{cases} f(-2)>0 &~\cdots\cdots① \\[4pt] f(2)>0 &~\cdots\cdots② \\[4pt] 軸:-2<a<2 &~\cdots\cdots③ \\[4pt] 判別式:D>0 &~\cdots\cdots④ \end{cases} \end{align*}
1つずつ解いていこう。 $f(-2)=5a+4$ であるから,①より \begin{align*} &5a+4>0 \\[4pt] &a>-\dfrac{4}{5}~\cdots\cdots①’ \end{align*}
$f(2)=-3a+4$ であるから,②より \begin{align*} &-3a+4>0 \\[4pt] &a<\dfrac{4}{3}~\cdots\cdots②’ \end{align*}
④より \begin{align*} &\dfrac{D}{4}=a^2-a>0 \\[4pt] &a(a-1)>0 \\[4pt] &a<0,~1<a~\cdots\cdots④’ \end{align*}

したがって,求める $a$ の値の範囲は
\begin{align*} -\dfrac{4}{5}<a<0,~1<a<\dfrac{4}{3} \end{align*}

ヒロ
解の配置問題では,青丸で示した解を考えるのではなく,赤丸で示した端点の上下と頂点の上下左右の位置を考えるようにしよう。




















